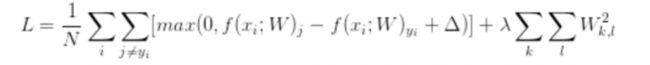cs231n-svm作业
cs231n-svm作业
svm
- cs231n-svm作业
-
- 1.基础概念
-
- 1.1 向量重构
- 1.2 种类和样本数
- 2.非向量化求导和loss
-
-
- 2.1svm理解
- 2.2svm求loss
- 2.3svm求导
- 3.向量化求导和求loss
-
- 3.1向量化求loss
- 3.2向量和求dw
-
1.基础概念
1.1 向量重构
X_train = np.reshape(X_train, (X_train.shape[0], -1))
这样就设置乘 n* 3073 的二位向量
因为图像的大小为32*32 * 3 =3072的rgb图像,这样就把一张图全部转化为一行
之所以是3073,3073=3072+1
因为 y=wx+b,b是列向量,可以简化为x在最后一列新加一列全1的列向量,这样就可以变成
y=x.w,最后输出n*10
1.2 种类和样本数
num_classes = W.shape[1]
num_train = X.shape[0]
第一个是预测是哪一种的,第二个是有多少张图片。
2.非向量化求导和loss
2.1svm理解
svm的公司如下
Δ一般设置为1。
公式的含义是,物品的真实值在本次预测中是否比其他的预测远远大于1,如果是的,那么损失就是0.不是,那么就是损失。剩下的是惩罚函数。让参数值越小越好。
2.2svm求loss
loss = 0.0
for i in range(num_train):
scores = X[i].dot(W)
correct_class_score = scores[y[i]]
for j in range(num_classes):
if j == y[i]:
continue
margin = scores[j] - correct_class_score + 1 # note delta = 1
字面上的意思,这里我们要排除掉本身减去本身会出现1,直接continue。
2.3svm求导
dw与w的外形一样,因为w要根据dw进行梯度更新。
请求到遵循链式法则
当且仅当,这个max成立,才能求导。等价于上面的margin>0。
对于非标签类的w求导。
因为是非标签类就等于(s2-s1)+(s0-s1.)s1是标签。s2,s0是非标签,对s2=w2x。s1=w1x
s0=w0x
我们是要对w求导。对w求导就是对w0,w1,w2求导.
以对w2求导为例,s2-s1,进行对s2求导,因为s2里有w2.
那就是1,s2=w2x,对w2求导那就是x,进行链式符合,复合相乘就是x。
那么
dW[:, j] += X[i]
按列更新。因为w0就是输出为0种类的向量。
对s1的更新同理,不过由于是s2-s1和s0-s1,那么就是对s1求导就是-1,整体对w1求导就是-x
dW[:,y[i]] += -X[i]
整体的代码如下:
num_classes = W.shape[1]
num_train = X.shape[0]
loss = 0.0
h = 0.00001
hW = W - h
for i in xrange(num_train):
scores = X[i].dot(W)
hscores = X[i].dot(hW)
correct_class_score = scores[y[i]]
for j in xrange(num_classes):
if j == y[i]:
continue
margin = scores[j] - correct_class_score + 1 # note delta = 1
if margin > 0:
loss += margin
dW[:,y[i]] += -X[i]
dW[:, j] += X[i]
# Right now the loss is a sum over all training examples, but we want it
# to be an average instead so we divide by num_train.
loss /= num_train
dW /= num_train
# Add regularization to the loss.
loss += reg * np.sum(W * W)
dW += 2 * reg * W # (1)
return loss, dW
注意不要忘记/num,这是loss更新的方法,再加上惩罚函数求导。
3.向量化求导和求loss
3.1向量化求loss
由上面的思想得知,我们首先要求出n个图像在这10个类上的得分就是n*10的矩阵。
那么,我们首先定义score = x。dot(w),这就是所有的得分。
其次,我们选出正确标签的得分,使用choose’函数,选出正确的分数,并且keepdims,让他保持二维矩阵。
scores_correct = scores[np.arange(num_train), y].T #N by 1
通过使用广播效应,我们可以进行加1,对所有的矩阵元素。
之后使用广播,我们可以把correct变成n*c,同时减去correct。
最后把score标签位置设置为0,并与0比大小,然后进行求和。
margins[np.arange(num_train), y] = 0.0
margins[margins <= 0] = 0.0
最后求和更新loss,整体代码如下:
scores = X.dot(W) # N by C
num_train = X.shape[0]
num_classes = W.shape[1]
scores_correct = scores[np.arange(num_train), y] #1 by N
scores_correct = np.reshape(scores_correct, (num_train, 1)) # N by 1
margins = scores - scores_correct + 1.0 # N by C
margins[np.arange(num_train), y] = 0.0
margins[margins <= 0] = 0.0
loss += np.sum(margins) / num_train
loss += 0.5 * reg * np.sum(W * W)
3.2向量和求dw
由上文可知,这是进行复核链式求导,那么我们先对s来进行求导。
由于max(s0-s1)+max(s2-s1),我们可以发现,只有成立时才可以进行求导。
成立时,进行求导,非标签类的s0,s2对本身求导就是1。标签类的s1的系数是-2,
我们可以发现s0+s2+s1=0,求导后的系数和就是-2,可以直接先求非标签类。
这就是对s进行求导
count_matrix = np.zeros(margins.shape)
count_matrix[margins > 0] = 1 # include j = y_i
count_column = np.sum(count_matrix, axis=1) # include j = y_i
count_matrix[np.arange(num_train), y] -= count_column # offset
由于是链式求导,s=wx,那么对w求导那就是x,最终就是w’ = s‘。x
s‘是count_matrix 是n * c ,x是n*3073,dw是3073 * c
我们可以用x。t。dot(s’),就行了。
最终代码如下:
count_matrix = np.zeros(margins.shape)
count_matrix[margins > 0] = 1 # include j = y_i
count_column = np.sum(count_matrix, axis=1) # include j = y_i
count_matrix[np.arange(num_train), y] -= count_column # offset
dW = X.T.dot(count_matrix)
dW /= num_train
dW += 2 * reg * W