论文阅读笔记:A Scalable Exemplar-based Subspace ClusteringAlgorithm for Class-Imbalanced Data
ECCV 2018
Chong You, Chi Li, Daniel P. Robinson, Rene Vidal
的子空间聚类方法由于其经验上的成功和理论上的保证,已成为无监督学习的常用工具。然而,它们的性能可能会受到不平衡数据分布和大规模数据集的影响。本文提出了一种基于样本的子空间聚类方法来解决大规模数据集的不平衡问题。
通过计算表示系数的![]() 范数,所提出的方法搜索最能代表所有数据点的数据集子集。为了有效地求解我们的模型,我们引入了一种最远优先搜索算法,该算法迭代地选择代表性最差的点作为样本。当数据来自子空间的并集时,我们证明了即使数据是不平衡的,计算的子集也包含足够多的来自每个子空间的样本来表示所有数据点。我们的实验表明,在两个不平衡的大规模图像数据集中,该方法优于现有的子空间聚类方法。我们还证明了我们的方法在人脸图像分类任务的无监督数据子集选择上的有效性。
范数,所提出的方法搜索最能代表所有数据点的数据集子集。为了有效地求解我们的模型,我们引入了一种最远优先搜索算法,该算法迭代地选择代表性最差的点作为样本。当数据来自子空间的并集时,我们证明了即使数据是不平衡的,计算的子集也包含足够多的来自每个子空间的样本来表示所有数据点。我们的实验表明,在两个不平衡的大规模图像数据集中,该方法优于现有的子空间聚类方法。我们还证明了我们的方法在人脸图像分类任务的无监督数据子集选择上的有效性。
1. 简介
不同类别的未标记数据集中的数据样本数量差异很大。因此,在无监督的学习任务中,处理不平衡的数据是一个重大挑战。传统的无监督学习方法利用了一个事实,即在许多计算机视觉应用中,数据的基本维度远小于环境维度,因此可以用低维子空间的并集来建模。子空间聚类是从此类数据中进行无监督学习的一种流行方法,它联合学习子空间的并集,并将每个数据点分配给相应的子空间。
本文贡献
我们提出了一种基于样本的子空间聚类方法来解决不平衡和大规模数据的问题。给定一个数据集![]() ,我们的想法是选择一个子集
,我们的想法是选择一个子集![]() ,我们称之为范例,并将每个数据点作为点在
,我们称之为范例,并将每个数据点作为点在![]() 中的线性组合写入(而不是在SSC中的
中的线性组合写入(而不是在SSC中的![]() ):
):
相比于标准的SSC,上式显然对不平衡数据集更加鲁棒(如果选择的子集是类别均衡的),此外,当![]() 相对于原始数据
相对于原始数据![]() 较小时,SSC能更有效地求解。因此,为了实现对不平衡数据的鲁棒性和对大型数据集的可伸缩性,我们需要一种高效的算法来选择在不同类之间更平衡的示例
较小时,SSC能更有效地求解。因此,为了实现对不平衡数据的鲁棒性和对大型数据集的可伸缩性,我们需要一种高效的算法来选择在不同类之间更平衡的示例![]() 。
。
在本文中,我们提出了一个新的模型来选择样本![]() ,该模型基于最小化数据
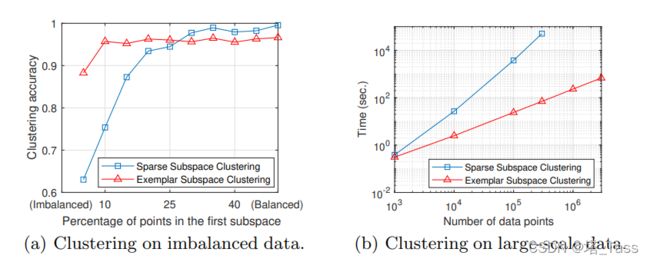
,该模型基于最小化数据![]() 的最大表示代价。此外,我们还介绍了一种有效的算法来解决具有线性时间和内存复杂性的优化问题。与SSC相比,基于样本的子空间聚类对不平衡数据不太敏感,对大数据更有效(见图1)。此外,我们的工作做出了以下贡献:
的最大表示代价。此外,我们还介绍了一种有效的算法来解决具有线性时间和内存复杂性的优化问题。与SSC相比,基于样本的子空间聚类对不平衡数据不太敏感,对大数据更有效(见图1)。此外,我们的工作做出了以下贡献:
- 我们对我们的样本选择模型和算法进行了几何解释,通过子集的Minkowski泛函,找到最能覆盖整个数据集所有类的子集。
- 我们证明,当数据位于独立子空间的并集时,我们的方法可以保证从每个子空间中选择足够多的数据点,并构造正确的数据亲和力,即使数据是不平衡的。
- 我们在两个不平衡的图像数据集上评估了我们的方法:EMNIST手写字母数据集和GTSRB街道标志数据集。实验结果表明,我们的方法在聚类性能和运行时间方面优于现有的方法。
2 相关工作
略
3 基于范例的子空间聚类(ESC)
我们首先建立了从![]() 中选择样本子集
中选择样本子集![]() 的模型。由于该模型是一个组合优化问题,我们提出了一种有效的近似求解算法。最后,我们描述了从示例
的模型。由于该模型是一个组合优化问题,我们提出了一种有效的近似求解算法。最后,我们描述了从示例![]() 生成聚类分配的过程。
生成聚类分配的过程。
3.1 基于自表示代价的样本选择
回想一下,在SSC中,每个数据点xj∈ X被写成所有其他数据点与系数向量![]() 的线性组合。而每个
的线性组合。而每个![]() 中的非零项确定了一个可以用来表出
中的非零项确定了一个可以用来表出![]() 的
的![]() 的子集,所有
的子集,所有![]() 的集合通常需要整个数据集
的集合通常需要整个数据集![]() 。在ESC中,目标是找到一个可以表示
。在ESC中,目标是找到一个可以表示![]() 中所有数据点的小子集
中所有数据点的小子集![]() 。特别地,集合
。特别地,集合![]() 应该包含来自每个子空间的样本,这样每个数据点的解都是子空间保持的。下面,我们根据(2)中的优化定义一个成本函数,然后给出我们的示例选择模型。
应该包含来自每个子空间的样本,这样每个数据点的解都是子空间保持的。下面,我们根据(2)中的优化定义一个成本函数,然后给出我们的示例选择模型。
定义1 自表示代价
几何上,![]() 定义了数据点
定义了数据点![]() 是否被很好地包含在子集
是否被很好地包含在子集![]() 中(见第4节)。函数
中(见第4节)。函数![]() 具有以下性质
具有以下性质
引理1: 函数是对集合单调的
即:![]()
区间的下界即只有一个点![]() ,有定理1知,上界来自于
,有定理1知,上界来自于![]() 。
。
因此我们建议通过搜索在限制子集![]() 的样本点的个数来执行样本选择使自表示成本函数最小化,即:
的样本点的个数来执行样本选择使自表示成本函数最小化,即:
其中![]() 为采样点的个数。通过如下引理可知
为采样点的个数。通过如下引理可知![]() 也是单调的。
也是单调的。
引理3:自表示损失(即函数的上界)对于集合是单调的
![]()
求解上述上界的最小化的优化问题是全局NP-hard的,它需要评估所有最大数目为k的所有子集![]() 对应的
对应的![]() 。在下一节,我们提出了一种高效的近似计算算法。
。在下一节,我们提出了一种高效的近似计算算法。
3.2 A Farthest First Search (FFS) for ESC
在算法1中我们近似地求解上述优化问题。
该方法逐步扩增初始为空集的候选子集知道包含k个点。对于每次迭代,如step 3所示,选择的点![]() 是当前子集
是当前子集![]() 最难线性表出的(即损失
最难线性表出的(即损失![]() 最大的),这暗合了引理2的要求,因为只有该点
最大的),这暗合了引理2的要求,因为只有该点![]() 或
或![]() 不属于子集时才能使当前的
不属于子集时才能使当前的![]() 损失最大。注意到FFS可以被看作最远优先遍历算法的一种扩展。
损失最大。注意到FFS可以被看作最远优先遍历算法的一种扩展。
高效的实现。每次迭代中。算法1需要评估所有点![]() 的
的![]() 。因此计算复杂度为是总样本点数N的线性关系(假设k确定且远小于N)。然而,计算
。因此计算复杂度为是总样本点数N的线性关系(假设k确定且远小于N)。然而,计算![]() 本身就是困难的,他需要求解一个稀疏优化问题。在接下来,我们提出了算法2来跳过某些点计算
本身就是困难的,他需要求解一个稀疏优化问题。在接下来,我们提出了算法2来跳过某些点计算![]() 的步骤。
的步骤。
这是因为引理2表明了![]() 是单调的,因此有
是单调的,因此有![]() 。在FFS算法中,子集
。在FFS算法中,子集![]() 的容量是不断增长的,这隐含着
的容量是不断增长的,这隐含着![]() 函数相对迭代次数i的增加是单调非增函数。在算法2的step 2中,我们对所有点相对于初始化后子集计算
函数相对迭代次数i的增加是单调非增函数。在算法2的step 2中,我们对所有点相对于初始化后子集计算![]() ,对于之后的所有迭代i,这是对应
,对于之后的所有迭代i,这是对应![]() 损失的上界。我们先对
损失的上界。我们先对![]() 进行排序
进行排序![]() ,使得
,使得![]() ,之后当按照该排序的数据点
,之后当按照该排序的数据点![]() 计算
计算![]() (step 7)的同时通过可变的max_cost跟踪
(step 7)的同时通过可变的max_cost跟踪![]() 的最大值(step 9)。我们可以根据该指标提前停止计算(setp 11),即,一旦
的最大值(step 9)。我们可以根据该指标提前停止计算(setp 11),即,一旦![]() 我们就可以断言任何index比
我们就可以断言任何index比![]() 更大的数据点都不能再最大化
更大的数据点都不能再最大化![]() ,从而避免了计算剩下点的
,从而避免了计算剩下点的![]() 。
。
3.3 从ESC得到聚类结果
4 实验
在本节中,我们将演示ESC在子空间聚类和无监督子集选择任务中的性能。计算自表示代价![]() 的步骤(如算法2的step 7)由SPAMS包中实现的LARS算法的LASSO版本解决。
的步骤(如算法2的step 7)由SPAMS包中实现的LARS算法的LASSO版本解决。
4.1 子空间聚类
数据集。Extended-MNIST(EMNIST)是MNIST数据集的扩展,它包含灰度的手写字母。我们将所有190998张对应于26个小写字母的图像作为26类聚类问题的数据。该数据集中每个图像的大小为28×28。之后,每个图像由散射卷积网络计算出的特征向量表示,该网络具有平移不变性和变形稳定性(即,它将小变形线性化)。因此,EMNIST的这些特征大致遵循子空间并集模型。
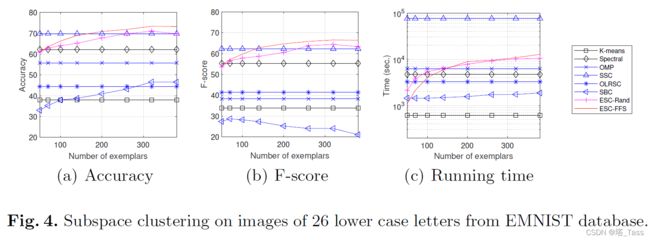
EMNIST是不均衡的。在EMNIST中,每个字母的图像数量从2213(字母“j”)到28723(字母“e”)不等,每个字母的样本数量大约等于它们在英语中的出现频率。
EMNIST的结果。下图显示了EMNIST的结果。从左到右,子图分别显示了作为样本数(X轴)函数的Acc、F-score和运行时间(Y轴)。回想一下,在SSC中,每个数据点都表示为所有其他点的线性组合。通过选择样本子集并使用这些样本表达点,当样本数达到200时,ESC-FFS能够优于SSC。相比之下,ESC-Rand的表现并没有显著优于SSC,这表明了FFS样本选择的重要性。在运行时间方面,我们发现ESC-FFS比SSC快很多。具体来说,ESC-FFS几乎与ESC-Rand一样有效,这表明所提出的FFS算法2是有效的。