决策树和随机森林的python实现

决策树

决策树是一种有监督的机器学习算法，该方法可以用于解决分类和回归问题。决策树可以简单地理解为达到某一特定结果的一系列决策。包含分类树（classification tree）和回归树(regression tree)。

实现方法

sklearn.tree模块中提供了很多关于决策树的类，tree.DecisionTreeClassifier可实现分类树模型，tree.DecisionTreeRegressor可实现回归树模型。

sklearn.tree.DecisionTreeClassifier(criterion="entropy" 	#不纯度的计算方法。"entropy"表示使用信息熵，ID3算法,此时sklearn实际计算的是基于信息熵的信息增益(Information Gain)；"gini"表示使用基尼系数，CART算法
     ,splitter="best" 	#控制决策树中的随机选项。“best”表示在分枝时会优先选择重要的特征进行分枝；“random”表示分枝时会更加随机，常用来防止过拟合
     ,max_depth=10	#限制树的最大深度，深度越大，越容易过拟合。
     ,min_samples_split=5 	#节点必须包含训练样本的个数。
     ,min_samples_leaf=1	#叶子最少包含样本的个数
     ,min_weight_fraction_leaf=0.0	#基于权重的剪枝参数，如果样本是加权的，则使用基于权重的预修剪标准来更容易优化树结构，这确保叶节点至少包含样本权重的总和的一小部分。
     ,max_features=None	#限制分枝的特征个数
     ,random_state=None	#输入任意数字会让模型稳定下来。加上random_state这个参数后，score就不会总是变化。随机性越大，效果一般越好，因此一般不设置，若追求稳定性可设置成固定值
     ,max_leaf_nodes=None 	#最大叶子节点数量，在最佳分枝下，以max_leaf_nodes为限制来生长树。默认没有节点数量的限制。
     ,min_impurity_decrease=0.0	#限制信息增益的大小，信息增益小于设定值分枝不会发生
     ,min_impurity_split=None 	#节点必须含有最小信息增益再划分
     ,class_weight=None	#设置样本的权重，当正反样本差别较大时，又需要对少的样本进行精确估计时使用，搭配min_weight_fraction_leaf来剪枝
     ,presort=False	#是否预先分配数据以加快拟合中最佳分枝的发现。在大型数据集上使用默认设置决策树时，将这个参数设置为True，可能会延长训练过程，降低训练速度。当使用较小数据集或限制树的深度时，设置这个参数为True，可能会加快训练速度。
                                 ）
                   

测试

from sklearn.tree import DecisionTreeClassifier
import pandas as pd
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import precision_score, recall_score, f1_score, confusion_matrix, classification_report
# 导入数据
iris=datasets.load_iris()
X=pd.DataFrame(iris.data,columns=iris.feature_names)
Y=pd.DataFrame(iris.target,columns=['target'])
#分割测试集和训练集
Xtrain,Xtest,Ytrain,Ytest = train_test_split(X,Y,test_size=0.25,random_state=1)

#训练模型
tree_clf=DecisionTreeClassifier()
tree_clf=tree_clf.fit(Xtrain,Ytrain)
Ypred = tree_clf.predict(Xtest)
train_score=tree_clf.score(Xtrain,Ytrain)
test_score=tree_clf.score(Xtest,Ytest)##导入测试集，由接口score得到模型的得分
print(f'train score: {train_score},  test score: {test_score}')

#测试集具体预测情况
confmat = confusion_matrix(y_true=Ytest, y_pred=Ypred)#输出混淆矩阵
print(confmat)# 混淆矩阵并可视化
# 查准率、查全率、F1值
print('precision:%.3f' % precision_score(y_true=Ytest, y_pred=Ypred,average= 'macro'))
print('recall:%.3f' % recall_score(y_true=Ytest, y_pred=Ypred,average= 'macro'))
print('F1:%.3f' % f1_score(y_true=Ytest, y_pred=Ypred,average= 'macro'))

更好地展示结果

from sklearn import tree
import matplotlib.pyplot as plt
# 对决策树进行美化并保存决策树图片到本地

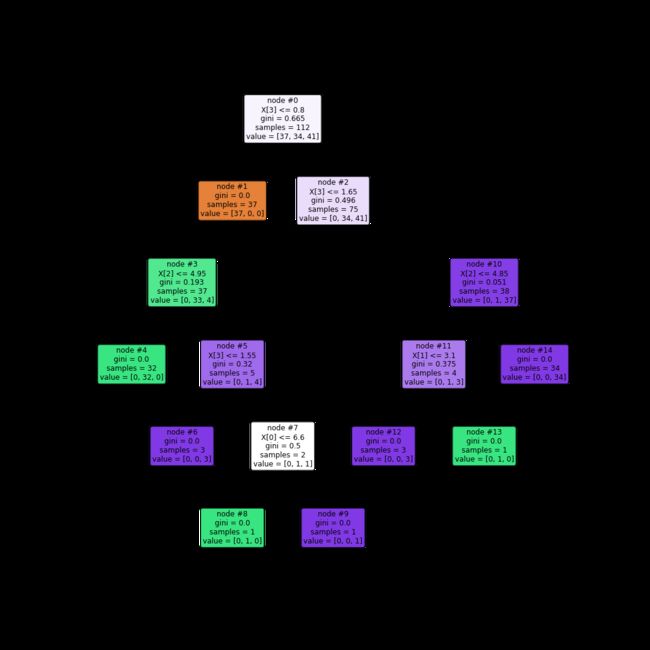
plt.figure(figsize=(15,15))      #设置画布大小（单位为英寸）
tree.plot_tree(tree_clf             #训练好的决策树评估器
               ,node_ids=True  #显示节点id
               ,filled=True    #给节点填充颜色
               ,rounded=True   #节点方框变成圆角
               ,fontsize=12    #节点中文本的字体大小
              )

plt.savefig("决策树.png")      #保存图片一定要在plt.show()之前
plt.show()

调参

scoring

对模型评价的scoring可设置的参数包括：accuracy、average_precision、f1、f1_micro、f1_macro、f1_weighted、f1_samples、neg_log_loss、roc_auc等

F1-score：是统计学中用来衡量二分类模型精确度的一种指标，用于测量不均衡数据的精度。它同时兼顾了分类模型的精确率和召回率。F1-score可以看作是模型精确率和召回率的一种加权平均，它的最大值是1，最小值是0。

在多分类问题中，如果要计算模型的F1-score，则有两种计算方式，分别为micro-F1和macro-F1，这两种计算方式在二分类中与F1-score的计算方式一样，所以在二分类问题中，计算micro-F1=macro-F1=F1-score，
micro-F1和macro-F1都是多分类F1-score的两种计算方式；
除了micro-F1和macro-F1，还有weighted-F1，是一个将F1-score乘以该类的比例之后相加的结果，也可以看做是macro-F1的变体吧。
micro-F1：多分类问题，若数据极度不平衡会影响结果；
macro-F1：多分类问题，不受数据不平衡影响，容易受到识别性高（高recall、高precision）的类别影响；
由于我们的问题是多分类问题，我们在这里采用f1_micro或者f1_macro。

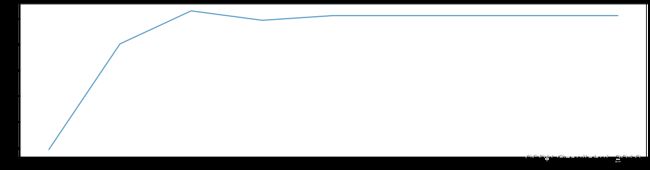
from sklearn.model_selection import cross_val_score
scorel = []
for i in range(1,10,1):
    #实例化决策树分类器
    #随机的模式为1
    dtc = DecisionTreeClassifier(max_depth=i,random_state=1)
    #使用交叉验证为我们的模型打分，然后求平均值
    score = cross_val_score(dtc,Xtrain,Ytrain,cv=10,scoring='f1_micro',n_jobs=-1).mean()
    #将我们的模型的分数追加到我们的结果列表中
    scorel.append(score)
##将列表中的最大值，也就是最好的打分打印出来
print(max(scorel),([*range(1,10)][scorel.index(max(scorel))]))
plt.figure(figsize=[20,5])
plt.plot(range(1,10,1),scorel)
plt.show()