【sklearn第十二讲】最近邻

机器学习训练营——机器学习爱好者的自由交流空间（入群联系qq：2279055353）

sklearn.neighbors提供了一组基于邻居的有监督和无监督学习方法。其中的无监督近邻是其它学习方法的基础，有监督近邻广泛应用于离散标签的分类和连续标签的回归。最近邻方法的基本原则是，找到事先定义样本数，距离新点最近的样本，从这些样本预测新点的标签。样本数可以是用户自定义的(k-nearest neighbor), 或者根据局部的点密度改变(radius-based neighbor). 通常，距离可以是任何测度，标准的欧氏距离是普遍的选择。尽管简单，最近邻已经被成功地应用到分类和回归问题，包括手写数字和卫星遥感图像识别。作为一种非参数方法，它经常能够成功地应用到决策边界不规则的分类里。

类sklearn.neighbors能接受Numpy数组或scipy.sparse矩阵作为输入。对于稠密矩阵，它支持很多距离测度；对于稀疏矩阵，它支持任何Minkowski距离。

无监督近邻

NearestNeighbors执行无监督的近邻学习。它作为三种不同的近邻算法：BallTree, KDTree, 和一个基于sklearn.metrics.pairwise的暴风算法的统一接口。近邻搜索算法的选择受关键词algorithm控制，该词可选值在[‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’]里。当取默认值auto时，算法试图从训练数据里确定最好的方法。

找到最近邻

对于在两个数据集之间找到最近邻这样的简单任务，可以使用sklearn.neighbors里的无监督算法。

from sklearn.neighbors import NearestNeighbors
import numpy as np
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
nbrs = NearestNeighbors(n_neighbors=2, algorithm='ball_tree').fit(X)
distances, indices = nbrs.kneighbors(X)
indices
distances

因为查询集匹配训练集，每一个点的最近邻就是该点自身，距离为0. 也可以产生一个稀疏图，表示邻近点的连接情况。

nbrs.kneighbors_graph(X).toarray()

在我们的数据集，下标顺序邻近的点，在参数空间里也是邻近的，这导致了k-近邻的块对角矩阵。

KDTree 与 BallTree 类

也可以使用KDTree, BallTree类直接找到最近邻。 Ball Tree and KD Tree有相同的接口，下面我们举一个KD Tree的例子。

from sklearn.neighbors import KDTree
import numpy as np
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
kdt = KDTree(X, leaf_size=30, metric='euclidean')
kdt.query(X, k=2, return_distance=False)

更多的选项信息，请参考KDTree, BallTree类文档。

最近邻分类

基于邻居的分类是一种基于实例的学习，它并不试图创建一个通用模型，而仅仅存储训练数据的实例。分类计算每一个点的近邻的大多数投票结果，即，一个待分类的点被分到它的大多数近邻所属的类。

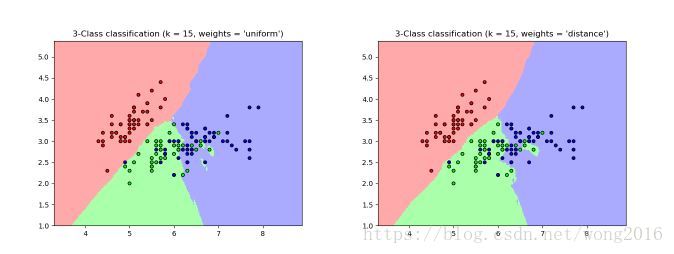
scikit-learn执行两个不同的近邻分类器。KNeighborsClassifier执行基于每一个待分类点的k近邻的学习，k是一个由用户确定的整数。最优的k值高度依赖数据：通常一个更大的k值抑制噪音的效果，却使分类边界不太清晰。

RadiusNeighborsClassifier执行基于每个训练点的固定半径r内的邻居数的学习，r是一个由用户确定的浮点数。当数据并不是均匀抽样时，这种方法是更好的选择。用户确定一个固定的半径r, 使得在稀疏邻居里的点使用更少的近邻分类。对于高维的参数空间，该方法不太有效。

基本的近邻分类使用一致的权，即，分派给一个查询点的值从它的近邻的大多数投票结果计算得到。在某些情况下，给邻居加权，使得更近的邻居对拟合贡献的更多。这可以通过关键词weights实现。默认weights = ‘uniform’, 即为每一个邻居分派一致的权。weights = ‘distance’, 为邻居分派与查询点的距离成反比例的权，即距离越大权越小。用户也可以自定义权函数。

最近邻回归

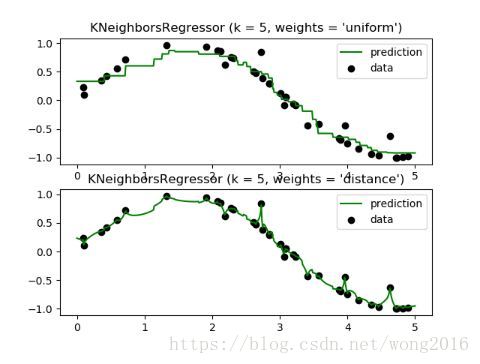
当数据标签是连续而不是离散的时候，可以使用基于邻居的回归。分派给一个查询点的标签，可以根据它的近邻标签的均值来计算。scikit-learn执行两种不同的邻居回归。KNeighborsRegressor执行基于每个查询点的k近邻的学习，k是由用户确定的整数。RadiusNeighborsRegressor执行基于查询点固定半径r内的邻居的学习，r是由用户确定的浮点值。

基本的近邻回归使用一致的权，即，在局部的邻居里的每一个点对一个查询点的分类贡献相等的权。在某些情况下，对邻居加权，使得邻近的点对回归的贡献多于相对远的点。这可以通过关键词weights实现。默认weights = ‘uniform’, 给所有的邻居分派相等的权。weights = ‘distance’, 为邻居分派与查询点的距离成反比例的权，即距离越大权越小。用户也可以自定义权函数。

多结果近邻回归的一个例子是"基于多结果估计量的人脸完成"。在这个例子里，输入X是人脸上半部分像素，输出Y是预测的人脸下半部分像素。

近邻算法

Brute Force

近邻的快速计算方法是机器学习领域的一个活跃的研究方向。最直接的邻居搜索执行数据集所有点对的暴风( brute-force)计算。对于 $D$ 维空间上的 $N$ 个样本，该方法的计算复杂度为 $O[D{N}^2]$. 有效的brute-force邻居搜索对于小的数据样本非常有竞争力，然而，随着样本数 $N$ 的增大，这种方法迅速变得不可行了。在类sklearn.neighbors里，使用关键词algorithm = 'brute’指定brute-force邻居搜索，使用sklearn.metrics.pairwise计算。

KD Tree

为了解决brute-force方法的计算效率问题，已经提出了很多基于树的数据结构。通常，这些树结构试图减少必要的距离计算数量，这主要通过有效地编码样本集成距离信息实现。基本思想是，如果点 $A$ 距离点 $B$ 很远，点 $B$ 距离点 $C$ 很近，那么点 $A$ 距离点 $C$ 也很远。这样，可以不必明确地计算 $A$ 与 $C$ 的距离。用这种方式，一个近邻搜索的计算代价减少为 $O[DN\log N]$ 甚至更好。对于大 $N$ 的 brute-force搜索，这是一个显著的改善。

一个利用集成信息的方法是KD树结构(k-dimensional tree)。它推广二维Quad-trees和三维Oct-trees到任何维度。KD树是一个二值树结构，它沿着数据轴递归地分割参数空间。构建一棵KD树非常快，这是因为分割仅沿着数据轴做，不需要计算 $D$ 维距离。而一旦建好了一棵树，只需要 $O[\log N]$ 的距离计算就能确定一个查询点的近邻。尽管KD树方法对于一个查询点的低维($D<20$)邻居搜索非常快，但是当维数 $D$ 变大时，它的效率就不高了。在scikit-learn里，KD树邻居搜索使用关键词algorithm = 'kd_tree’指定，由类KDTree计算。

Ball Tree

为了解决KD树在高维执行效率低的问题，提出了Ball Tree数据结构。KD树沿着笛卡儿轴分割数据，ball树沿着嵌套的超球分割数据。这种分割代价比KD树要高，但对于高维数据集，结果非常有效。

一棵ball树递归地分割数据进入中心 $C$, 半径 $r$ 的节点里，使得节点里的每一个点位于由 $C,r$ 定义的超球内。一次邻居搜索的候选点数减少了，通过使用三角不等式：

$$|x+y|\le |x|+|y|$$

这样，计算一个检验点和中心的距离就足够确定节点里的所有点的距离的上、下界。因为ball树节点的球形几何特征，在高维情况，它的表现优于KD树。在scikit-learn里，基于ball树的邻居搜索由关键词algorithm = 'ball_tree’指定，由类sklearn.neighbors.BallTree执行。用户也可以直接使用类BallTree.

近邻算法的选择

给定一个数据集，最优算法的选择是一个复杂的问题，依赖很多因素。

样本数 $N$ 与维数 $D$

• Brute force搜索算法时间随 $O[DN]$ 增长

• Ball tree搜索算法时间大致随 $O[D\log N]$ 增长

• KD tree搜索算法时间随 $D$ 改变。对于小 $D$ ($D\le 20$), 代价大致是 $O[D\log N]$, 此时KD tree更有效。对于大 $D$, 代价几乎增长到 $O[DN]$,

对于小样本数据集 ($N<30$), $\log N$ 与 $N$ 是可比的，这时brute force算法比基于树的方法更有效。KDTree和BallTree通过提供一个leaf size参数解决这个问题。该参数控制样本数量，使搜索及时转到Brute force. 这样一来，两种树算法接近一个Brute force算法在小样本时的效率。

数据结构：数据的本征维数与稀疏性

本征维数(intrinsic dimensionality)是指用多少个特征可以表示一个样本，对于一个 $D$ 维样本，它的本征维数 $d$ 满足： $d\le D$. 稀疏性是指数据填充参数空间的程度，它有别于稀疏矩阵的概念。数据矩阵没有0项，但结构仍有可能是稀疏的。

• Brute force算法查询时间不受数据结构影响。

• Ball tree and KD tree算法查询时间受数据结构影响较大。通常，具有较小本征维数和较稀疏的数据，查询时间更快。机器学习使用的数据倾向于结构化的，因此更适合基于树的查询算法。

查询点的邻居数 $k$

• Brute force算法基本不受 $k$ 值的影响

• Ball tree and KD tree算法查询时间变慢，随着 $k$ 的增大。

查询点的数量

ball tree and the KD Tree都需要一个建树阶段。当查询是分别进行时，这个建树阶段可以忽略不计。如果只查询少量的点，建树过程在整个代价里占显著的比例。如果只查询几个点， brute force比其它两种树方法更好。

阅读更多精彩内容，请关注微信公众号：统计学习与大数据