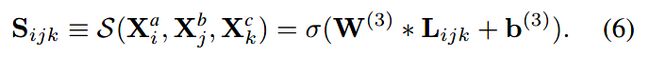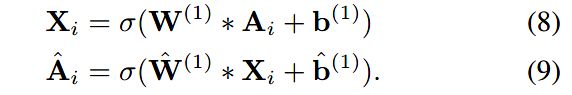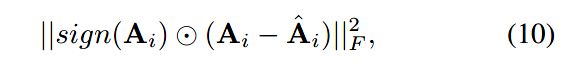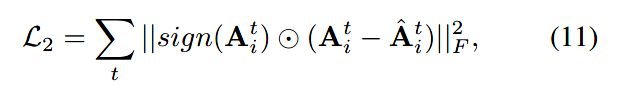【论文解读 AAAI 2018 | DHNE】Structural Deep Embedding for Hyper-Networks

论文链接：https://arxiv.org/abs/1711.10146

代码链接：https://github.com/tadpole/DHNE

会议：AAAI 2018

---

目录

1 摘要

2 介绍

2.1 一些基本概念如下

2.2 本文的贡献如下

2.3 一些定义

3 Deep Hyper-Network Embedding

3.1 损失函数

4 总结

---

1 摘要

现有的网络嵌入工作都聚焦于有成对关系的网络，但在现实中，有超边（hyperedge）的存在，例如三个或者更多个节点由一个超边相关联起来。当超边不可分解时，也就是说hyperedge中任意的节点子集都不能形成另一个hyperedge，如何对hyper-network编码成为了需要解决的问题。

本文提出了DHNE模型（Deep Hyper-Network Embedding），以学习有着不可分解的hyperedges的网络的嵌入表示。作者从理论上证明了现有方法中常用的嵌入空间的线性相似度度量不能保持超网络的不可分解性。所以提出了一个新模型，实现非线性的tuplewise的相似度度量，同时在形成的嵌入空间中保留局部和全局的相似性。

2 介绍

现有的绝大多数网络嵌入方法都是为一般的pairwise network设计的，即每条边仅连接一对节点。然而在现实的应用中，节点之间的关系是比较复杂的，超越了pairwise。例如，John买了一个棉质的衬衫，这就形成了一个high-order relationship：。由这种high-order relationships组成的网络就是hyper-network。

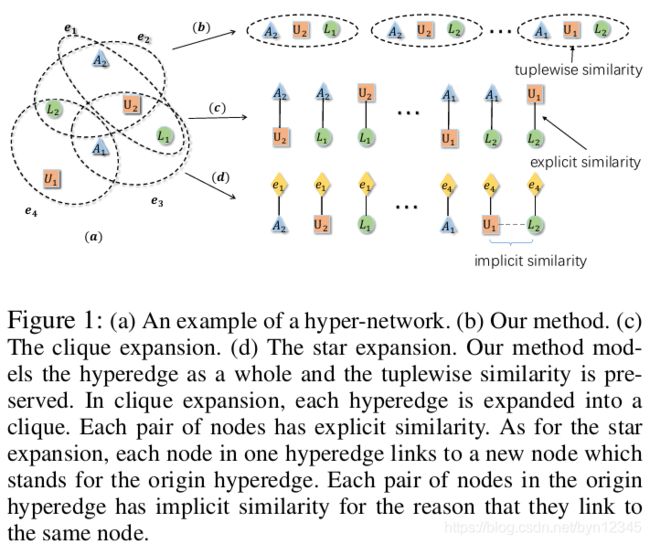
比较经典的处理hyper-network的方法是将其扩展为传统的pairwise network，然后再在上面应用分析算法，比如clique扩展法和star扩展法。但是这些方法都假定hyperedges是可分解的。三种方法的区别如下图所示：

2.1 一些基本概念如下

（1）不可分解性

异质的hyper-networks中的hyperedges通常是不可分解的，一个hyperedge是由紧密相关的一组节点组成的，也就是说节点的任何一个的子集，彼此之间都没有这么强的关联，也就不能组成另一个hyperedge。例如，推荐系统中的hyperedge为，但是之间的关系就没有那么强。这就意味着不能简单地使用传统的扩展方法将hyperedge分解。

（2）结构保存

如何在hyper-network中同时捕获和保存局部和全局的结构信息，仍是一个有待解决的问题。

为了解决不可分解性的问题，作者设计了不可分解的tuplewise的相似性函数，并且理论证明了它不能是线性函数。所以使用了深度神经网络和一个非线性激活函数来让其高度非线性。为了解决保存结构的问题，作者设计了一个深层自编码器，通过重构邻域结构，确保有相似邻域结构的节点也有相似的嵌入表示，来学习得到节点的表示。tuplewise的相似性函数和自编码器同时联合优化来解决上述的两个问题。

2.2 本文的贡献如下

（1）本文研究了经常被学术界忽略的有关不可分解的hyper-network的表示学习问题。提出了DHNE模型解决这一问题，并且能同时解决hyperedge的不可分解性以及保留丰富的结构信息。这一方法的复杂度和节点数量成线性关系，可扩展应用到大型网络中。

（2）理论证明了任何线性度量的嵌入空间都不能保留hyper-network不可分解的属性。

2.3 一些定义

（1）Hyper-network

一个hypergraph定义为，其中V是节点集合，有T种类型，，为边的集合，每个边由多于2个节点组成，。边的类型是边中所有节点类型的组合。若，则该hyper-netowrk是异质的。

（2）The First-order Proximity of Hyper-network

衡量了节点之间N-tuplewise的相似性。对于N个节点，如果存在一个hyperedge包含了这N个节点，则这N个节点的一阶相似性为1。而且这N个节点的任意子集都没有一阶相似性。

一阶相似性体现了不可分解性，但是由于网络的不完整性和稀疏性，还需考虑高阶相似性以捕获全局结构信息。

（3）The Second-order Proximity of Hyper-network

二阶相似性衡量了给定邻域结构的两点之间的相似性。对于任意节点表示节点的邻居。如果的邻居和的邻居相似，则的向量表示也和的相似。

3 Deep Hyper-Network Embedding

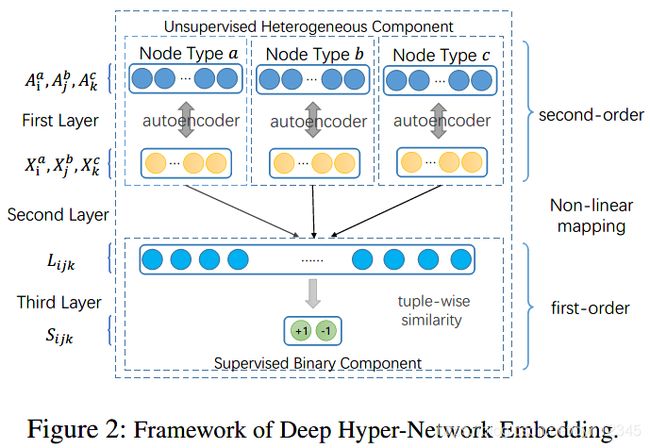
DHNE模型结构如下：

3.1 损失函数

为了保留hyper-network的一阶相似性，需要设计出能在嵌入空间衡量N-tuplewise相似性的函数。

性质一：作为节点的嵌入表示，S作为N-tuplewise相似性函数。若，则应该大于阈值l；若，则应该小于阈值s。

接着作者证明了线性的tuplewise相似性函数不能满足性质一，所以作者采用了多层感知机方法。

感知机由两部分组成，如图二的second layer和third layer所示。Second layer是使用非线性激活函数的全连接层，输入为三节点的向量表示，将其拼接并通过非线性函数映射到隐层空间L上，如下式所示：

获得后，最后在third layer将其映射到概率空间，以获得相似度：

将以上两层结合就得到了非线性的tuplewise的相似性衡量函数S。为了让该函数符合性质一，目标函数表示为如下形式：

其中，若之间有hyperedge，则为1，反之为0。若为1，则应该越大越好，反之越小越好。这也就保留了一阶相似性。

图二中的first layer是用于保留二阶相似性的。二阶相似性衡量的是邻居结构的相似性。作者定义了hyper-network的邻接矩阵捕获节点的邻域结构。对于hypergraph G=(V,E)， |V|*|E|大小的矩阵H作为输入，当时，h(v, e)=1。节点的度为，表示节点的度组成的对角矩阵。图G的邻接矩阵A定义为：

                                                                                         

邻接矩阵A中的元素表示了两个节点的共现次数，每一行表示了一个节点的邻域结构。作者将矩阵A作为输入特征，使用自编码器模型，从而保留邻域结构。自编码器由编码器和解码器组成，编码器通过非线性映射，把特征空间A映射到了隐层表示空间X；解码器通过非线性映射，将隐层表示空间X映射回原始的特征空间。具体过程如下：

自动编码器的目的是最小化输入和输出的重构误差，这一重构过程会使得有相似邻域的节点也有相似的隐层表示，实现了二阶相似性的保留。

但是邻接矩阵通常是非常稀疏的，为了加速模型，作者只对矩阵中的非零元素进行重构，重构误差如下：

由于异质网络中的节点类型多样，不同类型的节点有不同的特质，也就需要为不同类型的节点建立不同的隐层空间。所以自编码器的数量为节点类型的数量，即为不同类型的节点分配不同的自编码器。所以损失函数修正如下，t为节点类型的索引：

将一阶相似性和二阶相似性的损失函数结合起来，整个模型的目标函数如下：

因为网络中只有正向的关系，所以算法会最终收敛到所有tuplewise的关系都相似。为了解决这一问题，作者基于噪声分布，为每个边进行负采样。综上，算法如下所示：

4 总结

本文提出了DHNE模型，可解决带有不可分解的hyperedges的异质网络的表示学习问题。并且在理论上证明了现有的使用线性相似度的方法，不能保持hyper-networks的不可分解性。所以作者提出了非线性的tuplewise的相似度计算函数，并且同时保留了节点的局部和全局的相似度。在四种类型的hyper-networks上进行了实验，都取得了超越state-of-the-art的效果。

作者还进行了算法复杂度的分析，训练过程的复杂度和节点数量成线性关系。