【LeetCode 刷题笔记 2022-10-21】
2022-10-21 笔记
- 901. 股票价格跨度(每日一题)
-
- 1. 题目
- 2. 示例
- 3. 注意事项
- 4. Python 代码
- 77. 组合
-
- 1. 题目
- 2. 示例
- 3. 注意事项
- 4. Python 代码
- 5. 评测结果
- 39. 组合总和
-
- 1. 题目
- 2. 示例
- 3. 注意事项
- 4. Python 代码
- 5. 评测结果
- 40. 组合总和 II
-
- 1. 题目
- 2. 示例
- 3. 注意事项
- 4. Python 代码
- 5. 评测结果
- 216. 组合总和 III
-
- 1. 题目
- 2. 示例
- 3. 注意事项
- 4. Python 代码
- 5. 评测结果
- 377. 组合总和 Ⅳ
-
- 1. 题目
- 2. 示例
- 3. 注意事项
- 4. Python 代码
- 5. 评测结果
- 总结
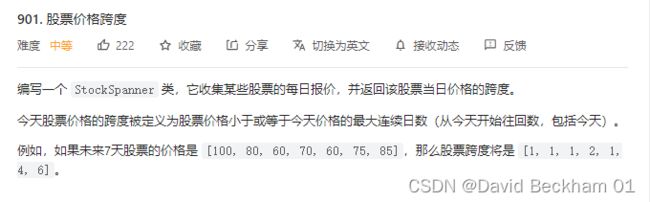
901. 股票价格跨度(每日一题)
1. 题目
2. 示例
示例 1:
输入:["StockSpanner","next","next","next","next","next","next","next"], [[],[100],[80],[60],[70],[60],[75],[85]]
输出:[null,1,1,1,2,1,4,6]
解释:
首先,初始化 S = StockSpanner(),然后:
S.next(100) 被调用并返回 1,
S.next(80) 被调用并返回 1,
S.next(60) 被调用并返回 1,
S.next(70) 被调用并返回 2,
S.next(60) 被调用并返回 1,
S.next(75) 被调用并返回 4,
S.next(85) 被调用并返回 6。
注意 (例如) S.next(75) 返回 4,因为截至今天的最后 4 个价格
(包括今天的价格 75) 小于或等于今天的价格。
3. 注意事项
- 难度:中等题
- 解题思路:
- 使用单调栈的方式解决当前问题, 具体解法如下
- 初始化时, 往栈中添加一个天数为 -1, 价格为 int 的最大值的元素, 保证不会栈空
- 每次调用 next 时, 先将栈中元素 股票价格 小于等于 当前股票价格 的元素弹出
- 当遇到栈中 股票价格 大于 当前股票价格 的元素, 计算出天数差并返回
- 注意:
- 栈中的元素结构为 (day, price), day: 表示当前日期(下标), price: 表示当前的股票价格
- 要先将当前节点入栈, 然后
self.day += 1,不然会出现除了第一个节点答案正确,其他节点的答案均少一天的情况
- 解题思路:
- 提示:
- 调用 StockSpanner.next(int price) 时,将有 1 <= price <= 10^5。
- 每个测试用例最多可以调用 10000 次 StockSpanner.next。
- 在所有测试用例中,最多调用 150000 次 StockSpanner.next。
- 此问题的总时间限制减少了 50%。
- 来源:力扣(LeetCode)
- 链接:传送门
- 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
4. Python 代码
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time : 2022/10/21 10:33
# @Author : David
# @File : 901. 股票价格跨度.py
# @Description : 901. 股票价格跨度
"""
编写一个 StockSpanner 类,它收集某些股票的每日报价,并返回该股票当日价格的跨度。
今天股票价格的跨度被定义为股票价格小于或等于今天价格的最大连续日数(从今天开始往回数,包括今天)。
例如,如果未来7天股票的价格是 [100, 80, 60, 70, 60, 75, 85],那么股票跨度将是 [1, 1, 1, 2, 1, 4, 6]。
解题思路:
1. 使用单调栈的方式解决当前问题, 具体解法如下
2. 初始化时, 往栈中添加一个天数为 -1, 价格为 int 的最大值的元素, 保证不会栈空
2. 每次调用 next 时, 先将栈中元素 股票价格 小于等于 当前股票价格 的元素弹出
3. 当遇到栈中 股票价格 大于 当前股票价格 的元素, 计算出天数差并返回
注意: 栈中的元素结构为 (day, price), day: 表示当前日期(下标), price: 表示当前的股票价格
提示:
调用 StockSpanner.next(int price) 时,将有 1 <= price <= 10^5。
每个测试用例最多可以调用 10000 次 StockSpanner.next。
在所有测试用例中,最多调用 150000 次 StockSpanner.next。
此问题的总时间限制减少了 50%。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/online-stock-span
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
"""
import sys
class StockSpanner:
def __init__(self):
# 2. 初始化时, 往栈中添加一个天数为 -1, 价格为 int 的最大值的元素, 保证不会栈空
self.stack = [(-1, sys.maxsize)]
self.day = 0 # 当前天数, 从第 0 天开始计数
def next(self, price: int) -> int:
while self.stack[-1][1] <= price:
# 2. 每次调用 next 时, 先将栈中元素 股票价格 小于等于 当前股票价格 的元素弹出
self.stack.pop()
# 3. 当遇到栈中 股票价格 大于 当前股票价格 的元素, 计算出天数差并返回
pre_day = self.stack[-1][0] # 前一个元素的 日期
ans = self.day - pre_day # 天数差 = 当前天数 - 上一个大于当前股票价格的节点的 天数
self.stack.append((self.day, price)) # 当前节点入栈
self.day += 1 # 日期 加1
# 4. 返回计算出的天数差
return ans
if __name__ == '__main__':
obj = StockSpanner()
arr = [100, 80, 60, 70, 60, 75, 85]
for price in arr:
print(obj.next(price), end=', ')
77. 组合
1. 题目
2. 示例
示例 1:
输入:n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
示例 2:
输入:n = 1, k = 1
输出:[[1]]
3. 注意事项
- 难度:中等题
- 经典的回溯搜索题目
- 循环中的参数不能使用
start+1而是应该使用i+1,因为start在循环中没有变化,所以会出现非常多的重复结果 - 回溯的三部曲:
- 确定递归函数参数
- 确定递归结束条件
- 单次递归搜索过程
- 提示:
- 1 <= n <= 20
- 1 <= k <= n
- 来源:力扣(LeetCode)
- 链接:传送门
- 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
4. Python 代码
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time : 2022/10/21 14:44
# @Author : David
# @File : 77. 组合.py
# @Description : 77. 组合
from typing import List
"""
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
提示:
1 <= n <= 20
1 <= k <= n
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/combinations
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
"""
class Solution(object):
def combine(self, n: int, k: int) -> List[List[int]]:
result = []
path = []
def backtrack(start: int) -> None:
# 1. 确定递归参数
if len(path) == k:
# 2. 确定递归出口
# 这里需要使用深拷贝
result.append([num for num in path])
return
# 3. 确定每次操作
for i in range(start, n + 1):
path.append(i)
# 注意循环中的参数不能使用“start+1”而是应该使用“i+1”,因为start 在循环中没有变化,所以会出现非常多的重复结果
backtrack(i + 1)
path.pop()
backtrack(1)
return result
def Main(self):
n, k = 3, 2
print(self.combine(n, k))
if __name__ == '__main__':
Solution().Main()
5. 评测结果
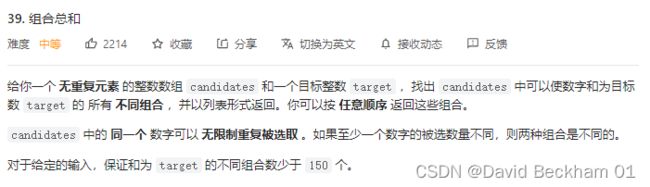
39. 组合总和
1. 题目
2. 示例
示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3:
输入: candidates = [2], target = 1
输出: []
3. 注意事项
-
难度:中等题
- 循环里面下一次循环的 start 需要传入 i
- 如果使用 i+1 或者 start+1 则表示不能重复选择,
-
提示:
- 1 <= candidates.length <= 30
- 2 <= candidates[i] <= 40
- candidates 的所有元素 互不相同
- 1 <= target <= 40
-
来源:力扣(LeetCode)
-
链接:传送门
-
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
4. Python 代码
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time : 2022/10/21 15:39
# @Author : David
# @File : 39. 组合总和.py
# @Description : 39. 组合总和
"""
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,
找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,
并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
提示:
1 <= candidates.length <= 30
2 <= candidates[i] <= 40
candidates 的所有元素 互不相同
1 <= target <= 40
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/combination-sum
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
"""
from typing import List
class Solution(object):
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
result = []
path = []
def backtrack(total: int, start: int) -> None:
if total >= target:
# 总和大于或等于目标值, 不需要继续往下递归了
if total == target:
# 如果满足要求, 添加到 result 中
result.append([num for num in path])
return
else:
for i in range(start, len(candidates)):
# 循环里面下一次循环的 start 需要传入 i ,
# 如果使用 i+1 或者 start+1 则表示不能重复选择,
x = candidates[i]
total += x
path.append(x)
backtrack(total, start + 1)
path.pop()
total -= x
# for i, x in enumerate(candidates):
# # 如果每次重新遍历 candidates, 虽然可以重复选择, 但是会出现多次重复的答案
# total += x
# path.append(x)
# backtrack(total, start + 1)
# path.pop()
# total -= x
backtrack(0, 0)
return result
def Main(self):
candidates = [2, 3, 6, 7]
target = 7
print(self.combinationSum(candidates, target))
if __name__ == '__main__':
Solution().Main()
5. 评测结果
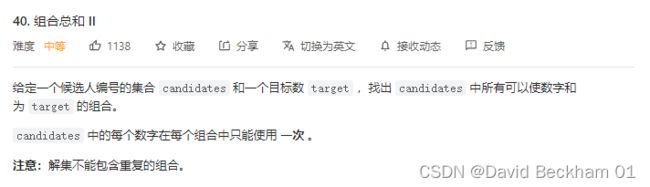
40. 组合总和 II
1. 题目
2. 示例
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]
3. 注意事项
- 难度:中等题
- 方法一,直接使用回溯,但是会超时
- 因为 candidates 的长度最长可以是
100所以需要使用剪枝,不然会出现超时的情况
- 因为 candidates 的长度最长可以是
- 方法二,使用回溯 + 剪枝
- 引用了LeetCode官方的题解,目前对这个题解还没有弄懂,接下来会仔细研究这个题解实现的原理
- 方法一,直接使用回溯,但是会超时
- 提示:
- 1 <= candidates.length <= 100
- 1 <= candidates[i] <= 50
- 1 <= target <= 30
- 来源:力扣(LeetCode)
- 链接:传送门
- 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
4. Python 代码
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time : 2022/10/21 17:09
# @Author : David
# @File : 40. 组合总和 II.py
# @Description : 40. 组合总和 II
from collections import Counter
from typing import List
"""
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
提示:
1 <= candidates.length <= 100
1 <= candidates[i] <= 50
1 <= target <= 30
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/combination-sum-ii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
"""
def func_1(candidates: List[int], target: int) -> List[List[int]]:
"""
方法一,回溯, 会超时
:param candidates: 待选择的数
:param target: 目标值
:return: 找出 candidates 中所有可以使数字和为 target 的组合
"""
sum_ca = sum(candidates)
if sum_ca < target:
return []
elif sum_ca == target:
return [candidates]
candidates.sort() # 从小到大排序
result = []
path = []
def backtrack(total: int, start: int) -> None:
if total >= target:
# 总和大于或等于目标值, 不需要继续往下递归了
if total == target:
# 如果满足要求, 添加到 result 中
result.append([num for num in path])
return
else:
for i in range(start, len(candidates)):
# 循环里面下一次循环的 start 需要传入 i+1
x = candidates[i]
total += x
path.append(x)
backtrack(total, i + 1)
path.pop()
total -= x
backtrack(0, 0)
# 目前得到的 result 还存在有重复的结果, 需要进行去重操作
temp_result = set() # 使用 set 去重
for arr in result:
t = ''
for num in arr:
t = f"{t},{num}"
temp_result.add(t)
result = []
for num in temp_result:
t = [int(x) for x in num.split(',')[1:]]
result.append(t)
return result
def func_2(candidates: List[int], target: int) -> List[List[int]]:
"""
方法二,回溯 + 剪枝
:param candidates: 待选择的数
:param target: 目标值
:return: 找出 candidates 中所有可以使数字和为 target 的组合
"""
freq = sorted(Counter(candidates).items())
ans = list()
sequence = list()
def dfs(pos: int, rest: int):
nonlocal sequence
if rest == 0:
ans.append(sequence[:])
return
if pos == len(freq) or rest < freq[pos][0]:
return
dfs(pos + 1, rest)
most = min(rest // freq[pos][0], freq[pos][1])
for i in range(1, most + 1):
sequence.append(freq[pos][0])
dfs(pos + 1, rest - i * freq[pos][0])
sequence = sequence[:-most]
dfs(0, target)
return ans
class Solution(object):
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
return func_2(candidates, target)
def Main(self):
candidates = [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1]
target = 30
print(self.combinationSum2(candidates, target))
if __name__ == '__main__':
Solution().Main()
5. 评测结果
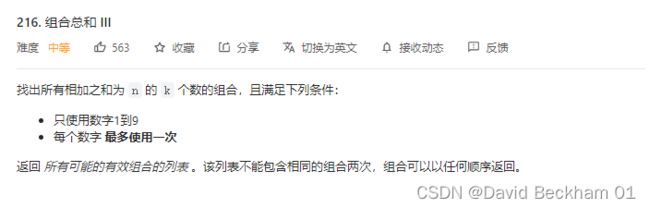
216. 组合总和 III
1. 题目
2. 示例
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。
示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。
示例 3:
输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字,我们可以得到的最小和是1+2+3+4 = 10,因为10 > 1,没有有效的组合。
3. 注意事项
- 难度:中等题
- 提示:
- 2 <= k <= 9
- 1 <= n <= 60
- 来源:力扣(LeetCode)
- 链接:传送门
- 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
4. Python 代码
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time : 2022/10/21 11:26
# @Author : David
# @File : 216. 组合总和 III.py
# @Description : 216. 组合总和 III
from typing import List
"""
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
1. 只使用数字1到9
2. 每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
提示:
2 <= k <= 9
1 <= n <= 60
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/combination-sum-iii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
"""
class Solution(object):
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
result = [] # 结果集合
path = [] # 当前路径
def backtrack(total: int, start: int) -> None:
"""
回溯寻找答案
图示(盗用的别人的图, 哈哈~): https://img-blog.csdnimg.cn/20201123195717975.png
:param total: 当前 path 的和
:param start: 当前开始的位置
:return: None
"""
if len(path) == k:
# 如果遍历的深度已经到达k
if total == n:
# 这里需要使用深拷贝, 不然会出现问题
result.append([num for num in path])
return
for i in range(start, 10):
total += i
path.append(i)
backtrack(total, i + 1)
path.pop()
total -= i
min_value = (k * (k + 1)) // 2 # 最大可以达到的数字
max_value = 45 - ((9 - k) * (10 - k)) // 2
if n < min_value or max_value < n:
# 如果 n 比最大能达到的数组还大 或者 n 比最小值还小, 则表示不存在这种组合可以满足条件
return []
else:
backtrack(0, 1)
# 返回结果集
return result
def Main(self):
k = 3
n = 9
print(self.combinationSum3(k, n))
if __name__ == '__main__':
Solution().Main()
5. 评测结果
377. 组合总和 Ⅳ
1. 题目
2. 示例
示例 1:
输入:nums = [1,2,3], target = 4
输出:7
解释:
所有可能的组合为:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意,顺序不同的序列被视作不同的组合。
示例 2:
输入:nums = [9], target = 3
输出:0
3. 注意事项
-
难度:中等题
- xxx
-
提示:
- 1 <= nums.length <= 200
- 1 <= nums[i] <= 1000
- nums 中的所有元素 互不相同
- 1 <= target <= 1000
-
来源:力扣(LeetCode)
-
链接:传送门
-
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
4. Python 代码
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time : 2022/10/21 20:16
# @Author : David
# @File : 377. 组合总和 Ⅳ.py
# @Description : 377. 组合总和 Ⅳ
from typing import List
"""
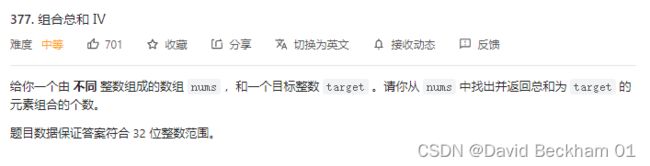
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。
请你从 nums 中找出并返回总和为 target 的元素组合的个数。
题目数据保证答案符合 32 位整数范围。
提示:
1 <= nums.length <= 200
1 <= nums[i] <= 1000
nums 中的所有元素 互不相同
1 <= target <= 1000
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/combination-sum-iv
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
"""
def func_1(nums: List[int], target: int) -> int:
"""
方法一:动态规划
思路:
1. 定义 dp[x] 表示选取元素之和等于 x 的方案数
2. 从定义中可以得知, dp[0] = 1, 最后返回的结果为 dp[target]
3. dp[i] = 所有 dp[i- num] 的和, num 是 nums 中的每一个元素
:param nums: 可选的数
:param target: 目标值
:return: 从 nums 中找出并返回总和为 target 的元素组合的个数。
"""
# 创建一个长度为 target + 1 的数组
dp = [0] * (target + 1) # 初始化数组
# 初始化 dp[0] = 1
dp[0] = 1
for i in range(1, len(dp)):
# 开始填写 dp 数组
for num in nums:
if i >= num:
dp[i] += dp[i - num]
return dp[target]
class Solution(object):
def combinationSum4(self, nums: List[int], target: int) -> int:
return func_1(nums, target)
def Main(self):
nums = [1, 2, 3]
target = 4
print(self.combinationSum4(nums, target))
if __name__ == '__main__':
Solution().Main()
5. 评测结果
总结
- 动态规划还是不是很会,例如:今天练习的
377. 组合总和 Ⅳ,判断不了什么时候该用动态规划。怎么设 dp,应该用一维数组还是二维数组,数组中的值表示什么意思… - 回溯的方法还需要多练习,尤其是
回溯 + 剪枝,例如:今天练习的40. 组合总和 II回溯好用,但是容易超时,所以问题规模比较小可以直接回溯不用剪枝,但是如果规模比较大则必须使用剪枝,不然会超时 - 回溯的三部曲:
- 确定递归函数参数
- 确定递归结束条件
- 单次递归搜索过程
- 还需要多刷题,关于
动态规划(普通动态规划、数位动态规划)、回溯 + 剪枝、背包问题(01背包、完全背包)、树、图、搜索(深度优先搜索、广度优先搜索)、排序(快速排序、插入排序)、栈、队列、堆、哈希表的题目还需要多练习、多巩固。 - 大佬文章:
- 希望用一种规律搞定背包问题
- 数位 DP 通用模板 + 详细注释 + 题单(Python/Java/C++/Go)
- 【宫水三叶】经典「数位 DP + 二分」运用题
- Leetcode 题解 - 动态规划.md