论文阅读：Spatial Transformer Networks

1 概述

CNN的机理使得CNN在处理图像时可以做到transition invariant，却没法做到scaling invariant和rotation invariant。即使是现在火热的transformer搭建的图像模型(swin transformer, vision transformer)，也没办法做到这两点。因为他们在处理时都会参考图像中物体的相对大小和位置方向。不同大小和不同方向的物体，对网络来说是不同的东西。这个问题在这篇文章统称为spatially invariant问题。甚至不同方向的物体，本身就真的是不同的东西，比如文字。

其实pooling layer有一定程度上解决了这个问题，因为在做max pooling或者average pooling的时候，只要这个特征在，就可以提取出来，在什么位置，pooling layer是不关心的。但是pooling的kernel size通常都比较小，需要做到大物体的spatially invariant是很难的，除非网络特别深。

STN(spatial transformer network)的提出，就是为了解决spatially invariant问题这个问题。它的主要思想很简单，就是训练一个可以把物体线性变换到模型正常的大小和方向的前置网络。这个网络可以前置于任何的图像网络中，即插即用。同时也可以和整个网络一起训练。

再说的直白一点，就是一个可以根据输入图片输出仿射变换参数的网络。

图1-1 STN结果示例

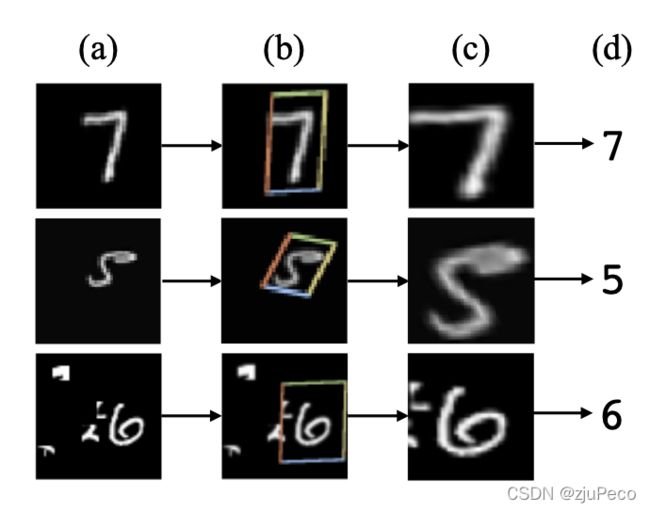
图1-1是STN网络的一个结果示意图，图1-1(a)是输入图片，图1-1(b)是STN中的localisation网络检测到的物体区域，图1-1©是STN对检测到的区域进行线性变换后输出，图1-1(d)是有STN的分类网络的最终输出。

2 模型说明

STN(spatial transformer network)更准确地说应该是STL(spatial transformer layer)，它就是网络中的一层，并且可以在任何两层之间添加一个或者多个。如下图2-1所示，spatial transformer主要由两部分组成，分别是localisation net和grid generator。

图2-1 stn模型结构示意图

2.1 Localisation Network

我们的目的是把第$l-1$层的第$n$行，第$m$列的特征移动到第$l$层的某行某列。如下图2-2所示，一个$3\times 3$的特征要变换的话，第$l$层的每个位置都可以表示为$l-1$层的特征的加权和。通过控制权重$w_{nm,ij}^l$就可以实现任何仿射变换。

图2-2 通过全连接进行仿射变换示例

但如果直接加一层全连接让模型学的话，模型可能学出来的就不是仿射变换了，参数量也很大，很难学，很难控制。所有就设计了一个localisation net，直接让模型学仿射变换的参数，这相当于是一个inductive bias。

localisation net的输入是前一层的特征，输出是仿射变换的参数，如果是平面的放射变换就是6个参数，通过这六个参数可以控制整个图像的平移，旋转，缩放。

图2-3 通过参数进行仿射变换示例

图2-3中的$[a,b,c,d,e,f]$参数就是localisation net的输出。核心公式就是

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{ccc}a& b& e\\ c& d& f\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]\text{\hspace{1em}(2-1)}$$

其中，$x$和$y$是当前层的坐标，$x^{\prime }$和$y^{\prime }$是前一层的坐标，$a$和$d$主要控制缩放，$b$和$c$主要控制旋转，$e$和$f$主要控制平移。

2.2 Parameterised Sampling Grid

localisation net输出了仿射变换参数之后，式$(2-1)$告诉了我们当前层$(x,y)$这个位置的特征是前一层的$(x^{\prime },y^{\prime })$位置的特征拿过来的。但是，如图2-4中的例子所示，$(x^{\prime },y^{\prime })$可能是小数，位置需要是正整数，如果采用取整的操作的话，网络就会变得不可梯度下降，没法更新参数了。

我们想要的是，当$[a,b,c,d,e,f]$发生微小的变化之后，下一层的特征也发生变化，这样才可以保证可以梯度下降。

图2-4 带插值的仿射变换示意图

于是，作者就采用了插值的方法来进行采样。比如当坐标为$[1.6,2.4]$时，就用$[a_{12}^{l-1},a_{13}^{l-1},a_{22}^{l-1},a_{23}^{l-1}]$这几个值进行插值。这样一来$[a,b,c,d,e,f]$发生微小的变化之后，$[x,y]$位置采样得到的值也会有变化了。这也使得spatial transformer可以放到任何层，跟整个网络一起训练。

3 模型效果

（1）文字识别任务
图3-1表示了STN加入到文字识别任务时带来的效果提升，图3-1左侧是不同模型在SVHN数据集上的错误率。这相当于是一个只有数字的文字识别任务。

图3-1 数字识别的效果示意图

不过用在OCR任务中，STN其实有点鸡肋。OCR有文字检测和文字识别两个部分，一般文字检测部分会带有检测框四个顶点的坐标，我们直接把文字检测的结果进行仿射变换再去文字识别就可以了，不需要在文字识别时再加一个STN。一个是难训练，再就是推理性能下降。

（2）图像分类任务
图3-2表示了STN在图像识别任务的效果，图3-2左侧表示了不同模型在Caltech-UCSD Birds-200-2011数据集上的准确率。

图3-2 数字识别的效果示意图

$2\times ST-CNN$表示在同一层是用了两个不同的STL，$4\times ST-CNN$表示在同一层是用了四个不同的STL。图3-2右侧中的方框表示了不同STL要进行放射变换的位置。

图3-3 鸟类识别中的STN示意图

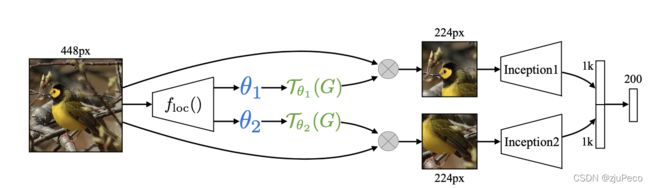
可以看到不同的STL关注的鸟的部位也是不一样的，一个一直关注头部，一个一直关注身子。这就相当于是一个attention，把感兴趣的区域提取出来了。

还有一个地方是，这里的方框都是正的，这其实是因为作者把仿射变换中的参数$[b,c]$人为置0了，变成了

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{ccc}a& 0& e\\ 0& d& f\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]\text{\hspace{1em}(3-1)}$$

可见STN是一个可以融入到很多图像模型，且可拓展性高的模块。

参考资料

[1] Spatial Transformer Networks
[2] 李宏毅-Spatial Transformer Layer