【机器学习】通过ID3,C4.5,CART算法构建决策树

（一）、决策树的简介

决策树(decision tree)是一种基本的分类与回归方法。决策树模型呈树形结构，在分类问题中，表示基于特征对实例进行分类的过程。它可以认为是if-then规则的集合，也可以认为是定义在特征空间与类空间上的条件概率分布。其主要优点是模型具有可读性，分类速度快。学习时，利用训练数据，根据损失函数最小化的原则建立决策树模型。预测时，对新的数据，利用决策树模型进行分类。决策树学习通常包括3个步骤：特征选择、决策树的生成和决策树的修剪。这些决策树学习的思想主要来源于由Quinlan在1986年提出的ID3算法和1993年提出的C4.5算法，以及由Breiman等人在1984年提出的CART算法。

决策树是一种树形结构，其中每个内部节点表示一个属性上的测试，每个分支代表一个测试输出，每个叶节点代表一种类别。决策树是一种十分常用的分类回归方法

简单来说决策树就是一棵树，其中跟节点和内部节点是输入特征的判定条件，叶子结点就是最终结果。

优点:计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特征数据。
缺点:可能会产生过度

（二）、构造决策树的三种构造方法

1.基于信息增益生成决策树（ID3算法）

信息增益是相对于特征而言的，信息增益越大，特征对最终的分类结果影响也就越大，我们就应该选择对最终分类结果影响最大的那个特征作为我们的分类特征。
提到信息增益必须先解释一下什么是“信息熵”，因为信息增益是基于信息熵而定义的。
信息熵的公式定义：

D：表示当前的数据集合。
k：表示当前数据集合中的第k类，也就是我们目标变量的类型。
这里根据公式算法得出一个数据集的信息熵

def calcShannonEnt(dataSet): 
    numEntries = len(dataSet)
    labelCounts = {}
    for featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key]) / numEntries
        shannonEnt -= prob * log(prob, 2)
    return shannonEnt

信息增益公式：
这里通过ID3算法选择信息增益最大的特征，结果返回信息增益的最大索引。

def splitdataSet(dataSet, axis, value):  # 分类数据
    retdataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]
            reducedFeatVec.extend(featVec[axis + 1:])
            # 去掉对应位置的特征
            retdataSet.append(reducedFeatVec)
    return retdataSet

def chooseBestFeatureToSplit(dataSet):  # 选择信息增益最大的特征
    numFeatures = len(dataSet[0]) - 1
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0
    bestFeature = -1
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        newEntropy = 0.0
        for value in uniqueVals:
            subdataSet = splitdataSet(dataSet, i, value)
            prob = len(subdataSet) / float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subdataSet)
        infoGain = baseEntropy - newEntropy
        if infoGain > bestInfoGain:
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature

导入自己的数据集，取数据集中的偶数项作为训练集，取奇数项作为测试集
下图为数据集中的某些数据展示，该数据为井字游戏残局数据集（数据集来源于UCI机器学习库）

def file_train(filename):  # 取数据集偶数作为训练集
    fr = open(filename)
    lines = fr.readlines()
    res = []
    i = 0
    for line in lines:
        line = line.strip()
        temp = line.split(",")
        if i % 2 == 0:  # 取总数据集里的偶数
            res.append(temp)
        i += 1
    labels = ["top-left-square", "top-middle-square", "top-right-square",
     "middle-left-square", "middle-middle-square", "middle-right-square",
     "bottom-left-square","bottom-middle-square","bottom-right-square"]
    return res, labels

def file_test(filename):  # 取数据集的奇数作为测试集
    fr = open(filename)
    lines = fr.readlines()
    res = []
    i = 0
    for line in lines:
        line = line.strip()
        temp = line.split(",")
        if i % 2 == 1:  # 取总数据集里的奇数
            res.append(temp)
        i += 1
    labels = ["top-left-square", "top-middle-square", "top-right-square", "middle-left-square", "middle-middle-square", "middle-right-square","bottom-left-square","bottom-middle-square","bottom-right-square"]
    return res, labels

运行结果：
生成的决策树

训练模型精度
可以看出基于信息增益训练出来的模型正确率为84.76%

2.基于信息增益率生成决策树（C4.5算法）

C4.5算法继承了ID3算法的优点，并在以下几方面对ID3算法进行了改进：

1) 用信息增益率来选择属性，克服了用信息增益选择属性时偏向选择取值多的属性的不足；
2) 能够完成对连续属性的离散化处理；
3) 能够对不完整数据进行处理。

优点：
产生的分类规则易于理解，准确率较高。
缺点：
在构造树的过程中，需要对数据集进行多次的顺序扫描和排序，因而导致算法的低效。此外，C4.5只适合于能够驻留于内存的数据集，当训练集大得无法在内存容纳时程序无法运行。
信息增益率公式：

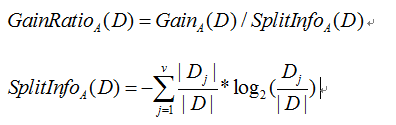
采用了一个启发式方法：先从候选划分属性中找出信 息增益高于平均水平的属性，再从中选取增益率最高的。

以下是C4.5算法代码，C4.5算法核心代码相较于ID3核心算法代码差距不大

def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1 
    baseEntropy = calcShannonEnt(dataSet)
    bestinfoGainratio = 0.0
    bestFeature = -1 
    for i in range(numFeatures):#遍历所有的特征
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList) 
        newEntropy = 0.0 
        IV = 0.0
        for value in uniqueVals:#遍历该特征维度下对应的所有特征值
            subDataSet = splitdataSet(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)#计算每个子集对应的信息熵，并全部相加，得到划分后数据的信息熵
            IV -= prob * log(prob,2)
        infoGain = baseEntropy - newEntropy#将原数据的信息熵-划分后数据的信息熵，得到信息增益
        if IV == 0.0:
            infoGainratio = 0.0
        else:
            infoGainratio = float(infoGain) / float(IV)
        if (infoGainratio > bestinfoGainratio):#如果这个信息增益率比当前记录的最佳信息增益率还大，就将该增益和划分依据的特征记录下来
            bestinfoGainratio = infoGainratio#更新信息增益率，找到最大的信息增益率
            bestFeature = i
    return bestFeature

运行结果：
生成的决策树

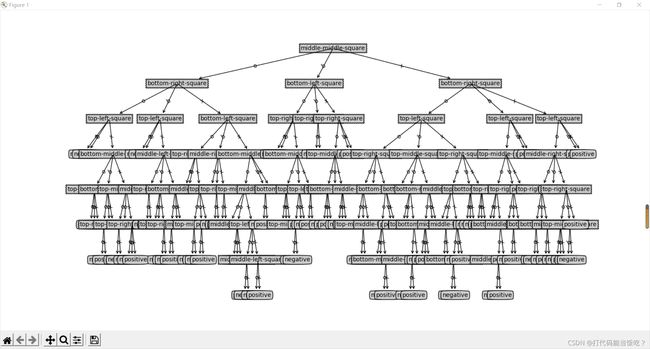
训练模型精度
由实验结果可以看出基于信息增益率训练出的模型正确率达到86.22%，相较于信息增益训练出来的模型正确率高了近2个百分点。

3.基于基尼指数生成决策树（CART算法）

CART（Classification And Regression Tree）分类回归树算法的最优特征选择方法
对于C4.5算法，我们也提到了它的不足，比如模型是用较为复杂的熵来度量，使用了相对较为复杂的多叉树，只能处理分类不能处理回归等。对于这些问题， CART算法大部分做了改进。

基尼指数，又称基尼不纯度，其计算和信息熵的类似，但是计算的速度会超过信息熵，因为没有计算对数的操作。基尼不纯度为这个样本被选中的概率乘以它被分错的概率，可以作为衡量不确定性大小的标准。当一个节点中所有样本都是一个类时，基尼不纯度为0。

对于给定的样本集合D，其基尼指数为：

将样本分为D1、D2，即将该属性的一个属性值抽出与其它属性值进行概率分布基尼指数的计算。该基尼指数表示经过特征A的某个取值分割集合D后的不确定性。

CART算法实现：

def calcProbabilityEnt(dataSet):
    numEntries = len(dataSet)
    feaCounts = 0
    fea1 = dataSet[0][len(dataSet[0])-1]
    for feaVec in dataSet:
        if feaVec[-1] == fea1:
            feaCounts += 1
    probabilityEnt = float(feaCounts) / numEntries
    return probabilityEnt
    
#选择最好的数据集划分方式
def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1  #特征数量，numfeature为特征的维度，因为最后一列为标签，所以需要减去1
    if numFeatures == 1: 
        return 0
    bestGini = 1     #最佳基尼指数
    bestFeature = -1     #最优的划分特征初始化为-1
    for i in range(numFeatures):   #遍历所有的特征
        featList = [example[i] for example in dataSet]
        feaGini = 0    #定义特征的值的基尼系数
        uniqueVals = set(featList) 
        for value in uniqueVals: #遍历该特征维度下对应的所有特征值
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            probabilityEnt = calcProbabilityEnt(subDataSet)
            feaGini += prob * (2 * probabilityEnt * (1 - probabilityEnt))
        if (feaGini < bestGini):
            bestGini = feaGini
            bestFeature = i   #记录基尼指数最小的索引值
    return bestFeature

运行截图：
生成的决策树

训练模型精度
可以看出基于基尼指数训练出来的模型精准度为83.3%。

总结

在ID3算法中我们使用了信息增益来选择特征，信息增益大的优先选择。
在C4.5算法中，采用了信息增益比来选择特征，以减少信息增益容易选择特征值多的特征的问题。
但是无论是ID3还是C4.5,都是基于信息论的熵模型的，这里面会涉及大量的对数运算。
在CART算法中，CART分类树算法使用基尼系数来代替信息增益比，基尼系数代表了模型的不纯度，基尼系数越小，则不纯度越低，特征越好。这和信息增益(比)是相反的。