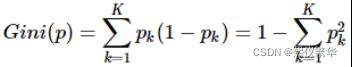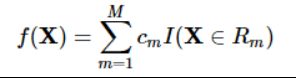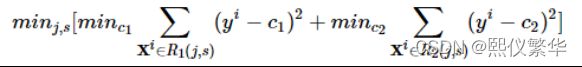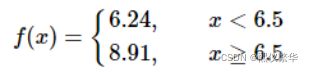机器学习算法22 决策树到集成学习思想(04 经典决策树算法 ID3和C4.5比较，CART)

1 ID3和C4.5比较

        ID3（Iterative Dichotomiser 3，迭代二叉树3代）由Ross Quinlan于1986年提出。1993年，他对ID3进行改进设计出了C4.5算法。

        我们已经知道ID3与C4.5的不同之处在于，ID3根据信息增益选取特征构造决策树，而C4.5则是以信息增益率为核心构造决策树。既然C4.5是在ID3的基础上改进得到的，那么这两者的优缺点分别是什么？

        使用信息增益会让ID3算法更偏向于选择值多的属性。信息增益反映给定一个条件后不确定性减少的程度，必然是分得越细的数据集确定性更高，也就是信息熵越小，信息增益越大。因此，在一定条件下，值多的属性具有更大的信息增益。而C4.5则使用信息增益率选择属性。信息增益率通过引入一个被称作分裂信息(Split information)的项来惩罚取值较多的属性，分裂信息用来衡量属性分裂数据的广度和均匀性。这样就改进了ID3偏向选择值多属性的缺点。

        相对于ID3只能处理离散数据，C4.5还能对连续属性进行处理，具体步骤为：

1. 把需要处理的样本(对应根节点)或样本子集(对应子树)按照连续变量的大小从小到大进行排序。
2. 假设该属性对应的不同的属性值一共有N个，那么总共有N−1个可能的候选分割阈值点，每个候选的分割阈值点的值为上述排序后的属性值中两两前后连续元素的中点，根据这个分割点把原来连续的属性分成bool属性。实际上可以不用检查所有N−1个分割点。(连续属性值比较多的时候，由于需要排序和扫描，会使C4.5的性能有所下降。)
3. 用信息增益比率选择最佳划分。

C4.5其他优点

1）在树的构造过程中可以进行剪枝，缓解过拟合

2）能够对连续属性进行离散化处理（二分法）；

3）能够对缺失值进行处理；

C4.5缺点：

      构造树的过程需要对数据集进行多次顺序扫描和排序，导致算法低效；

    刚才我们提到 信息增益对可取值数目较多的属性有所偏好；而信息增益率对可取值数目较少的属性有所偏好！OK，两者结合一下就好了！

解决方法：先从候选属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。而不是大家常说的直接选择信息增益率最高的属性！

2 CART

      CART（Classification And Regression Tree，分类回归树）由L.Breiman，J.Friedman，R.Olshen和C.Stone于1984年提出，是一种应用相当广泛的决策树学习方法。值得一提的是，CART和C4.5一同被评为数据挖掘领域十大算法。

        CART算法采用一种二分递归分割的技术，将当前的样本集分为两个子样本集，使得生成的的每个非叶子节点都有两个分支。因此，CART算法生成的决策树是结构简洁的二叉树。

        作为一种决策树学习算法，CART与ID3以及C4.5不同，它使用基尼系数（Gini coefficien）对属性进行选择。我们曾提及基尼系数的计算公式：

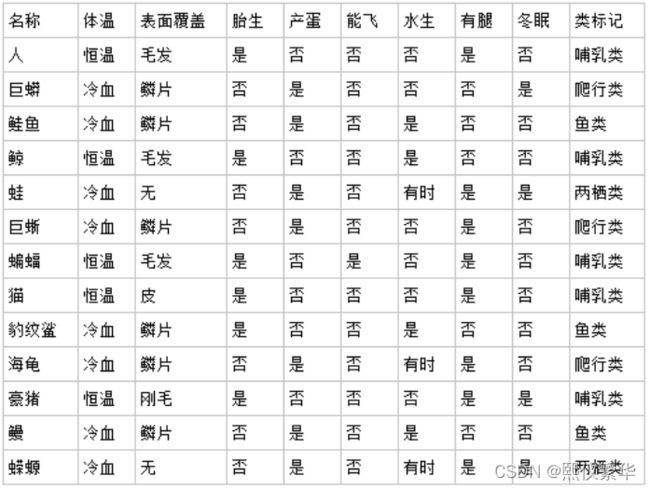
 举个例子，假设我们拥有如下表所示的动物分类信息表：

        那么对于非恒温动物，包含爬行类3个、鱼类3个、两栖类2个，因此，

Gini1=1-[（3/8）^2 + （3/8）^2 +（2/8）^2 ]

        而对于恒温动物，只包含5个哺乳类，同样，

Gini2=1 - 1^2 = 0

        同熵一样，如果样本集合D被某个属性A是否取某个值分成两个样本集合D1和D2，则在属性A的条件下，集合D的基尼指数定义为：

        对于上述按恒温和非恒温属性划分动物，

Gini(D, A)= 8/13 * Gini1 + 5/13 * Gini2

        在一定程度上基尼指数（Gini(D)）反应的是集合D的不确定程度，跟熵类似。Gini(D, A)反应的是经过特征A划分后集合D的不确定程度。基尼系数越大，样本集合的不确定性也就越大。因此最好的属性划分是使得Gini(D, A)最小的划分。

        下图显示了二分类问题中基尼系数、熵（单位比特）之半1/2*H(p)和分类误差率的关系。横坐标表示概率p，纵坐标表示损失。可以看出基尼系数和熵之半曲线很接近，都可以近似的代表分类误差率。

除了分类决策之外，CART也可以进行回归决策。

假设X和Y分别为输入和输出变量，Y为连续变量，训练数据集D为：

 一个回归树对应着输入空间的一个划分以及在划分的单元上的输出值。假设已经将输入空间划分为M个单元R1,R2,…,RM，在每个单元Rm上有个固定的输出Cm，则回归树表示为：

 

 问题是怎么对输入空间进行划分。一般采用启发式的思路，选择第 j 个Feature Xj和他的取值s分别作为切分变量（splitting variable）和切分点（splitting point），并定义两个区域：

 然后采用平方误差损失求解最优的切分变量j和切分点s。具体地，求解

每一个切分变量和切分点对(j,s)都将输入空间分成两个区域，然后分别求每个区域的输出值，使得误差最小，很显然输出值应该是那个区域所有样本值的平均值，即：

 举例说明，下面有一个简单的训练数据，根据这个数据集我们生成一棵回归树。

 由于x只有一个Feature，我们不用选择j，下面我们考虑如下的切分点s： 1.5，2.5，3.5，4.5，5.5，6.5，7.5，8.5，9.5 然后求出对应的R1,R2,c1,c2，以及总的误差：

经过计算，可以得到如下结果： 

很显然应该取s=6.5作为切分点，此时：

R1={1,2,3,4,5,6},R2={7,8,9,10},c1=6.24,c2=8.91

决策树为：

然后每个(j,s)对里找出使总误差最小的对作为最终的切分变量和切分点，对切分后的子区域重复这一步骤，直到满足停止条件为止。这样就生成了一颗回归树。此时的回归树成为最小二乘回归树（least squares regression tree）。

总结

        C4.5算法是在ID3算法的基础上采用信息增益率的方法选择决策属性。C4.5改进了ID3偏向选择值多属性以及只能处理离散属性等缺点。ID3算法和C4.5算法虽然在对训练样本集的学习中能尽可能多地挖掘信息，但其生成的决策树分支较大，规模较大。为了简化决策树的规模，提高生成决策树的效率，又出现了根据GINI系数来选择测试属性的决策树算法CART。

        CART算法采用一种二分递归分割的技术，与基于信息熵的算法不同，CART算法对每次样本集的划分计算GINI系数，GINI系数越小则划分越合理。CART算法总是将当前样本集分割为两个子样本集，使得生成的决策树的每个非叶结点都只有两个分枝。因此CART算法生成的决策树是结构简洁的二叉树。