python线性整数规划求解_Python Pulp包 整数线性规划

在学Optimisation的 时候用到了pulp包，在这里记录总结一下用法。

下面用两个例子来说明

物体移动最小距离问题

假设有n 个箱子和n个物体，箱子固定排列在x轴上，物体则分布在xy平面上，其中箱子和物体的初始位置均为已知。现要将物体放入箱子且使得每个箱子有且仅有一个物体，如何使得物体移动的距离最短？

可以定义

若物体j在箱子i中，否则为0，

为初始时物体j与箱子i间的距离, 则问题可以转变为

这是典型的整型规划问题，调用pulp包来解决

首先获取数据并得到距离矩阵M

import pulp as plp
import numpy as np

ca = open("PositionCasiers.txt")
ob = open("PositionObjets.txt")
clines = ca.readlines()[1:]
blines = ob.readlines()[1:]
nc = len(clines)
nb = len(blines)

# M est la matrice de distance pour bouger objet j dans la boîte i
M = np.zeros([nc,nb])

Cx = []
Cy = []
Ox = []
Oy = []
for i in range(nc):
    linec = clines[i].strip('n')
    linec = linec.split('t')
    cx = float(linec[0])
    cy = float(linec[1])
    Cx.append(cx)
    Cy.append(cy)
    
    for j in range(nb):
        lineb = blines[j].strip('n')
        lineb = lineb.split('t') 
        bx = float(lineb[0])
        by = float(lineb[1])
        Ox.append(bx)
        Oy.append(by)
        
        M[i,j] = np.sqrt((cx-bx)**2 + (cy-by)**2)

现在用c表示M矩阵，最后一行意思是将M写成问题数学描述里的

n = nc
m = nb
set_I = range(1, n+1)
set_J = range(1, m+1)
# c est le paramètre dans la formula 
c = {(i,j): M[i-1,j-1] for i in set_I for j in set_J}

定义解

cat参数意味着解的形式，由于该问题下x只能取0或1，因此选取binary，name取名字注意不要重复就行了

# x est de valeur binaire 
x_vars  = {(i,j):plp.LpVariable(cat=plp.LpBinary, name="x_{0}_{1}".format(i,j)) for i in set_I for j in set_J}

定义模型并添加限制

lpSum指求和

sense指限制形式有

三种，对应为LpConstraintEQ，LpConstraintLQ，LpConstraintGQ

e为等号（不等号）左边的式子

rhs为等号（不等号）右边的值

以第一个限制为例

for

in set_I 对应着

e对应

rhs对应1

sense=plp.LpConstraintEQ 对应 =

name注意不要和其他限制重名即可

# On constuit le model de MIP 
opt_model = plp.LpProblem(name="MIP Model")

# On rajoute la première contrainte
for i in set_I:
    opt_model.addConstraint(
    plp.LpConstraint(e=plp.lpSum(x_vars[i,j] for j in set_J),
                     sense=plp.LpConstraintEQ,
                     rhs=1,
                     name="constraintI{0}".format(i)))

# On rajoute la deuxième  contrainte
for j in set_J:
    opt_model.addConstraint(
    plp.LpConstraint(e=plp.lpSum(x_vars[i,j] for i in set_I),
                     sense=plp.LpConstraintEQ,
                     rhs=1,
                     name="constraintJ{0}".format(j)))        

定义目标以及优化方式，该问题中目标是

，故选取plp.LpMinimize

objective = plp.lpSum(x_vars[i,j] * c[i,j] for i in set_I for j in set_J)
opt_model.sense = plp.LpMinimize
opt_model.setObjective(objective)

求解

opt_model.solve()

导出结果到excel文件

opt_df = pd.DataFrame.from_dict(x_vars, orient="index", columns = ["variable_object"])
opt_df.index = pd.MultiIndex.from_tuples(opt_df.index, names=["column_i", "column_j"])
opt_df.reset_index(inplace=True)
opt_df["solution_value"] = opt_df["variable_object"].apply(lambda item: item.varValue)
opt_df.drop(columns=["variable_object"], inplace=True)
opt_df.to_csv("./optimization_solution.csv")

结果：

11意味着11号物体在一号位置，以此类推，15.377则为最短距离。

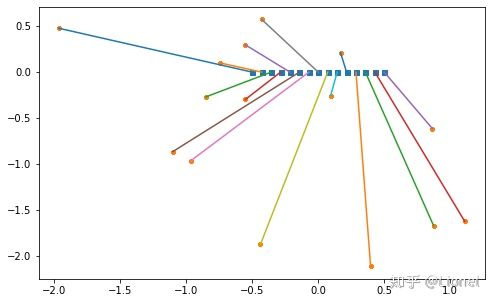
结果画出来如下，方块为箱子，原点为物体

plt.figure(0,figsize=(8,5))
plt.scatter(Cx, Cy, marker='s', s=25)
plt.scatter(Ox, Oy, s=10)
for i in range(len(p)):
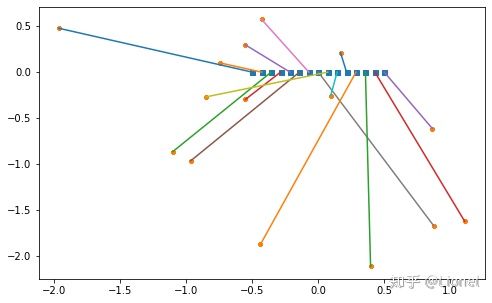
    plt.plot([Ox[p[i]-1],Cx[i]],[Oy[p[i]-1], Cy[i]])

所有的连线均不相交

若对问题增加限制，如4号物体所在箱子必须在3号箱子左边，则问题转变为

代码只需修改限制那一部分即可，注意model命名不要和以前一样

# On rajoute la première contrainte
for i in set_I:
    opt_model2.addConstraint(
    plp.LpConstraint(e=plp.lpSum(x_vars[i,j] for j in set_J),
                     sense=plp.LpConstraintEQ,
                     rhs=1,
                     name="2constraintI{0}".format(i)))
# On rajoute la deuxième contrainte
for j in set_J:
    opt_model2.addConstraint(
    plp.LpConstraint(e=plp.lpSum(x_vars[i,j] for i in set_I),
                     sense=plp.LpConstraintEQ,
                     rhs=1,
                     name="2constraintJ{0}".format(j)))
# On rajoute la troisième contrainte
for i in set_I:
    opt_model2.addConstraint(
    plp.LpConstraint(e=x_vars[i,3]+plp.lpSum(x_vars[i+k,4] for k in range(1,nc-i+1)),
                     sense=plp.LpConstraintLE,
                     rhs=1,
                     name="2constraintK{0}".format(i)))

结果为

工厂成本问题

现有一建筑公司需要租借机器，租用费用标准如下：

费用种类	费用	类型
配送至工地	800	/次
租金	200	/周
归还机器	1000	/次

该建筑公司需要保证每周工作机器数大于某数值，该数值为已知向量d，长度为n

现想要使得租用机器成本最低，则该如何租用机器？

若记

为第i周借入机器数，

为第i周归还机器数，则问题数学描述可写为：

为简化记号，记

，则有

读取数据

data = pd.read_csv('DonneesEnginsChantier.txt', sep='s+', header=None).values[0]
d = data
n = len(d)

定义模型及需要求解量x

model_Appro = plp.LpProblem("Appro", plp.LpMinimize)
x = ['x'+str(i) for i in range(2*n)]
for i in range(2*n):
    x[i] = plp.LpVariable('x{0}'.format(i), lowBound=0, cat='Integer')

将目标函数添加入模型

model_Appro += plp.lpSum([800*x[i] +1200*x[i+n] +200*plp.lpSum(x[j]-x[j+n] for j in range(i+1)) for i in range(n)])

添加限制

for k in range(1,n+1):
    model_Appro += plp.lpSum([x[i]-x[n+i] for i in range(k)]) >= d[k-1]

求解（解出值可通过 '参数名'.varValue获得，如x1.value, 具体可看作图部分）

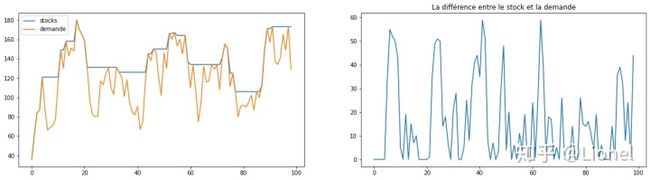
model_Appro.solve()

作图

values = []
for xi in x:
    values.append(xi.varValue)
s = np.array(values[:n])-np.array(values[n:])
stocks = [np.sum(s[:i+1]) for i in range(n)]
plt.figure(figsize=(20,5))
plt.subplot(1,2,1)
plt.plot(stocks,label='stocks')
plt.plot(d, label = 'demande')
plt.legend()
plt.subplot(1,2,2)
plt.plot(stocks-d)
plt.title('La différence entre le stock et la demande')

参考自

https://medium.com/opex-analytics/optimization-modeling-in-python-pulp-gurobi-and-cplex-83a62129807a