学习笔记六——循环神经网络
文章目录
-
- 一、序列模型
- 二、文本预处理
-
- 2.1 读取数据集
- 2.2 词元化(分词)
- 2.3 词表
- 2.4 整合所有功能
- 三、语言模型
-
- 3.1 统计算法:n-gram模型
- 二、RNN
-
- 2.1 RNN模型结构
- 2.2 RNN模型的缺点
- 二、长短时记忆网络LSTM
-
- 2.1 LSTM模型结构
- 2.2 双向循环神经网络Bi-LSTM
- 三、序列到序列模型
一、序列模型
之前讲的CNN更多的是处理空间信息,而序列模型(RNN、LSTM这一类)主要是处理时间信息。现实生活中,很多数据是有时序结构的。比如豆瓣的电影评分,不光是跟电影好坏有关,还会随时间的变化而变化:
- 拿奖后评分上升,直到奖项被忘记
- 看了很多好电影之后,人们的期望会变高
- 季节性:贺岁片、暑期档
- 导演。演员负面评价导致评分变低
序列数据还包括:
- 音乐、语言、文本、视频(都是连续的)
- 大地震之后可能会有余震
- 人的互动(比如网络互喷)
- 股价预测
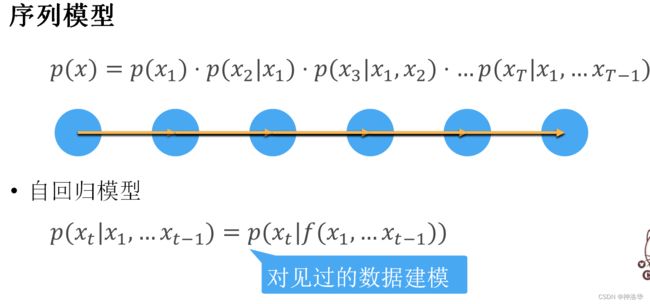
自回归模型:给定t个数据预测下一个数据,标签和样本是一个东西。常见是输入法输入、GPT-2。
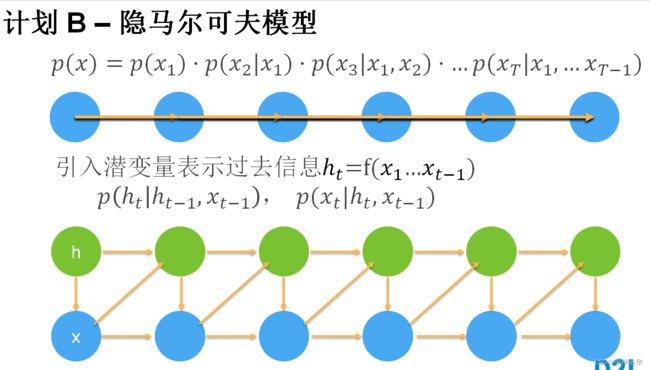
- 计划 A - 马尔可夫(Markov)假设:x出现的概率仅仅和τ个x有关。这样从变长数据预测变成定长数据预测,简化很多,用线性回归、MLP等等都行。
- 隐式马尔科夫模型(潜变量模型)。是保留一些对过去观测的总结 h t h_t ht,并且同时更新预测 x ^ t \hat{x}_t x^t和总结 h t h_t ht。这就产生了基于 x ^ t = P ( x t ∣ h t ) \hat{x}_t = P(x_t \mid h_{t}) x^t=P(xt∣ht)估计 x t x_t xt,以及公式 h t = g ( h t − 1 , x t − 1 ) h_t = g(h_{t-1}, x_{t-1}) ht=g(ht−1,xt−1)更新的模型。由于 h t h_t ht从未被观测到,这类模型也被称为隐变量自回归模型(latent autoregressive models)。
参考《学习笔记10:统计学习方法:——HMM和CRF》
二、文本预处理
文本是最常见序列之一。 例如,一篇文章可以被简单地看作是一串单词序列,甚至是一串字符序列。 本节中,我们将解析文本的常见预处理步骤。 这些步骤通常包括:
- 将文本作为字符串加载到内存中。
- 将字符串拆分为词元(如单词和字符)。
- 建立一个词表,将拆分的词元映射到数字索引。
- 将文本转换为数字索引序列,方便模型操作。
下面以H.G.Well的《时光机器》为例子进行介绍
2.1 读取数据集
首先,我们从H.G.Well的时光机器中加载文本。这是一个相当小的语料库,只有30000多个单词,下面的函数(将数据集读取到由多条文本行组成的列表中),其中每条文本行都是一个字符串。为简单起见,我们在这里忽略了标点符号和字母大写。
import collections
import re
from d2l import torch as d2l
d2l.DATA_HUB['time_machine'] = (d2l.DATA_URL + 'timemachine.txt',
'090b5e7e70c295757f55df93cb0a180b9691891a')
def read_time_machine(): #@save
"""将时间机器数据集加载到文本行的列表中"""
with open(d2l.download('time_machine'), 'r') as f:
lines = f.readlines()
return [re.sub('[^A-Za-z]+', ' ', line).strip().lower() for line in lines]
lines = read_time_machine()
print(f'# 文本总行数: {len(lines)}')
print(lines[0])
print(lines[10])
# 文本总行数: 3221
the time machine by h g wells
twinkled and his usually pale face was flushed and animated the
2.2 词元化(分词)
下面的tokenize函数将文本行列表(lines)作为输入,返回一个由词元(token)列表组成的列表,每个词元都是一个字符串(string)。 文本行列表中的每个元素是一个文本序列(如一条文本行), 每个文本序列又被拆分成一个词元列表。
def tokenize(lines, token='word'): #@save
"""将文本行拆分为单词或字符词元"""
if token == 'word':
return [line.split() for line in lines]
elif token == 'char':
return [list(line) for line in lines]
else:
print('错误:未知词元类型:' + token)
tokens = tokenize(lines)
2.3 词表
词元的类型是字符串,而模型需要的输入是数字,因此这种类型不方便模型使用。 现在,让我们[构建一个字典,通常也叫做词表(vocabulary), 用来将字符串类型的词元映射到从 0 开始的数字索引中]。
- 我们先将训练集中的所有文档合并在一起,对它们的唯一词元进行统计,得到的统计结果称之为语料(corpus)。
- 然后根据每个唯一词元的出现频率,为其分配一个数字索引。 很少出现的词元通常被移除,这可以降低复杂性。
- 语料库中不存在或已删除的任何词元都将映射到一个特定的未知词元“
”。 我们可以选择增加一个列表,用于保存那些被保留的词元, 例如:填充词元(“ ”); 序列开始词元(“ ”); 序列结束词元(“ ”)。
Tips:对token的次数进行排序,常用词就会在词表的开头,这样计算机会经常访问这一块的内容,读取会比较快,做embedding也会较好。(性能会好一点点)。类与对象参考《python学习笔记——类与对象、常用函数》
class Vocab: #@save
"""文本词表,reserved_tokens表示句子开始结尾的单词"""
def __init__(self, tokens=None, min_freq=0, reserved_tokens=None):
if tokens is None:
tokens = []
if reserved_tokens is None:
reserved_tokens = []
# 按出现频率排序
counter = count_corpus(tokens)
self.token_freqs = sorted(counter.items(), key=lambda x: x[1],
reverse=True)
# 未知词元的索引为0,uniq_tokens就是包含所有词的序列
self.unk, uniq_tokens= 0,['' ] + reserved_tokens
uniq_tokens+=[token for token,freq in self.token_freqs
if freq>min_freq and token not in uniq_tokens]
#下面就开始构造词和索引的词典self.token_to_idx
self.idx_to_token,self.token_to_idx=[],dict()
for token in uniq_tokens:
self.idx_to_token.append(token)#只是一个列表
self.token_to_idx[token] = len(self.idx_to_token) - 1
def __len__(self):
return len(self.idx_to_token)
def __getitem__(self, tokens):#给定token返回下标索引
if not isinstance(tokens, (list, tuple)):
return self.token_to_idx.get(tokens, self.unk)#找到返回下标,没找到返回的下标
return [self.__getitem__(token) for token in tokens]
def to_tokens(self, indices):#给定索引返回对应的token
if not isinstance(indices, (list, tuple)):
return self.idx_to_token[indices]
return [self.idx_to_token[index] for index in indices]
def count_corpus(tokens): #@save
"""统计词元的频率"""
# 这里的tokens是1D列表或2D列表,函数isinstance()可以判断一个变量的类型
if len(tokens) == 0 or isinstance(tokens[0], list):
# 将词元列表展平成一个列表
tokens = [token for line in tokens for token in line]
return collections.Counter(tokens)
我们首先使用时光机器数据集作为语料库来[构建词表],然后打印前几个高频词元及其索引。
vocab = Vocab(tokens)
print(list(vocab.token_to_idx.items())[:10],vocab.idx_to_token[:10])#类属性
print(vocab['the', 'i', 'and', 'of', 'a', 'to', 'was', 'in', 'that'])#vocab是字典,直接根据词得到索引
len(vocab),vocab.to_tokens([0,1,2,3,4,5,6,7,8,9,])#类方法
[('' , 0), ('the', 1), ('i', 2), ('and', 3), ('of', 4), ('a', 5), ('to', 6), ('was', 7), ('in', 8), ('that', 9)] ['' , 'the', 'i', 'and', 'of', 'a', 'to', 'was', 'in', 'that']
[1, 2, 3, 4, 5, 6, 7, 8, 9]
(4580, ['' , 'the', 'i', 'and', 'of', 'a', 'to', 'was', 'in', 'that'])
2.4 整合所有功能
在使用上述函数时,我们[将所有功能打包到load_corpus_time_machine函数中], 该函数返回corpus(词元索引列表)和vocab(时光机器语料库的词表)。 我们在这里所做的改变是:
- 为了简化后面章节中的训练,我们使用字符(而不是单词)实现文本词元化;
- 时光机器数据集中的每个文本行不一定是一个句子或一个段落,还可能是一个单词,因此返回的corpus仅处理为单个列表,而不是使用多词元列表构成的一个列表。
def load_corpus_time_machine(max_tokens=-1): #@save
"""返回时光机器数据集的词元索引列表和词表"""
lines = read_time_machine()
tokens = tokenize(lines, 'word')
vocab = Vocab(tokens)
# 因为时光机器数据集中的每个文本行不一定是一个句子或一个段落,
# 所以将所有文本行展平到一个列表中,corpus是词的索引
corpus = [vocab[token] for line in tokens for token in line]
if max_tokens > 0:
corpus = corpus[:max_tokens]
return corpus, vocab
corpus, vocab = load_corpus_time_machine()
len(corpus), len(vocab)#char模式下len(vocab)=28,这是指26个字母和unk以及空格
三、语言模型
参考李沐动手深度学习8.3《语言模型和数据集》
假设长度为 T T T的文本序列中的词元依次为 x 1 , x 2 , … , x T x_1, x_2, \ldots, x_T x1,x2,…,xT。 x t x_t xt( 1 ≤ t ≤ T 1 \leq t \leq T 1≤t≤T)可以被认为是文本序列在时间步 t t t处的观测或标签。在给定这样的文本序列时, 语言模型(language model)的目标是估计文本序列的联合概率
P ( x 1 , x 2 , … , x T ) . P(x_1, x_2, \ldots, x_T). P(x1,x2,…,xT).
例如,只需要一次抽取一个词元 x t ∼ P ( x t ∣ x t − 1 , … , x 1 ) x_t \sim P(x_t \mid x_{t-1}, \ldots, x_1) xt∼P(xt∣xt−1,…,x1),一个理想的语言模型就能够基于模型本身生成自然文本。
语言模型的应用包括:
- 预训练模型(BERT,GPT-3)
- 文本生成
- 判断一句文本是否正常
- 等等其它
3.1 统计算法:n-gram模型
参考《天池-新闻文本分类-task1机器学习算法》1.1 内容,这里就不写了
最大的优点是不论文本有多长,计算复杂度都是O(t),只是空间复杂度较高,要把所有n-gram存下来,n增大,存储量指数级增加。(但是实际中,去掉低频组合之后,n取较大也能用,比较长的序列有实际意义才会多次出现)
二、RNN
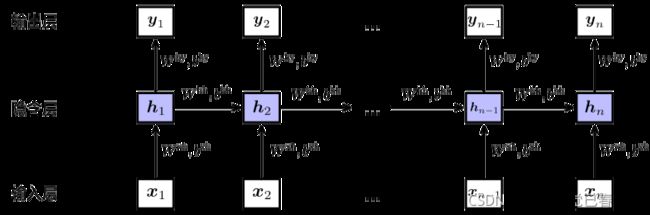
2.1 RNN模型结构
前馈神经网络:信息往一个方向流动。包括MLP和CNN
循环神经网络:信息循环流动,网络隐含层输出又作为自身输入,包括RNN、LSTM、GAN等。
RNN模型结构如下图所示:
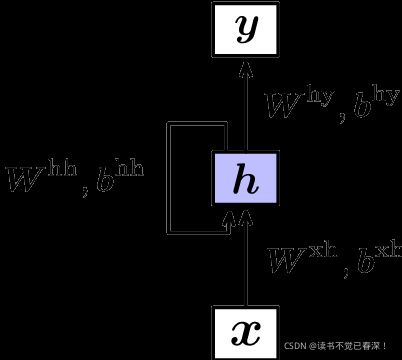
其输出为:
h t = t a n h ( W x h x t + b x h + W h h h t − 1 + b h h ) \mathbf {h_{t}=tanh(W^{xh}x_{t}+b^{xh}+W^{hh}h_{t-1}+b^{hh})} ht=tanh(Wxhxt+bxh+Whhht−1+bhh)
y n = s o f t m a x ( W h y h n + b h y ) \mathbf {y_{n}=softmax(W^{hy}h_{n}+b^{hy})} yn=softmax(Whyhn+bhy)
- 隐含层输入不但与当前时刻输入 x t x_{t} xt有关,还与前一时刻隐含层 h t − 1 h_{t-1} ht−1有关。每个时刻的输入经过层层递归,对最终输入产生一定影响。
- 每个时刻隐含层 h t h_{t} ht包含1~t时刻全部输入信息,所以隐含层也叫记忆单元(Memory)
- 每个时刻参数共享(‘循环’的由来)
- 使用tanh激活函数是因为值域(-1,1),能提供的信息比sigmoid、Relu函数丰富。
- 变长神经网络只能进行层标准化
- RNN处理时序信息能力很强,可以用于语音处理。NLP等
2.2 RNN模型的缺点
在前向传播时:
h t = t a n h ( W x h x t + b x h + W h h h t − 1 + b h h ) \mathbf {h_{t}=tanh(W^{xh}x_{t}+b^{xh}+W^{hh}h_{t-1}+b^{hh})} ht=tanh(Wxhxt+bxh+Whhht−1+bhh)
假设最后时刻为t,反向传播求对i时刻的导数为:
∂ L o s s ∂ W i h h = ∂ L o s s ∂ y t ⋅ ∂ y t ∂ h i ⋅ ∂ h i ∂ W i h h \mathbf {\frac{\partial Loss}{\partial W_{i}^{hh}}=\frac{\partial Loss}{\partial y_{t}^{}}\cdot \frac{\partial y_{t}^{}}{\partial h_{i}}\cdot \frac{\partial h_{i}^{}}{\partial W_{i}^{hh}}} ∂Wihh∂Loss=∂yt∂Loss⋅∂hi∂yt⋅∂Wihh∂hi
∂ h i ∂ W i h h = ( h i − 1 ) T \mathbf {\frac{\partial h_{i}}{\partial W_{i}^{hh}}=(h_{i-1})^T} ∂Wihh∂hi=(hi−1)T
∂ y t ∂ h i = ∂ y t ∂ h t ⋅ ∂ h t ∂ h i = ∂ y t ∂ h t ⋅ t a n h ′ ⋅ ∂ h t ∂ ( h t − 1 ) T ⋅ tanh ′ ⋅ ∂ h t − 1 ∂ ( h t − 2 ) T . . . ⋅ tanh ′ ⋅ ∂ h i + 1 ∂ ( h i ) T = ∂ y t ∂ h t ⋅ ( t a n h ′ ) t − i ⋅ W t − i \mathbf {\frac{\partial y_{t}}{\partial h_{i}}=\frac{\partial y_{t}}{\partial h_{t}}\cdot\frac{\partial h_{t}}{\partial h_{i}}=\frac{\partial y_{t}}{\partial h_{t}}\cdot tanh'\cdot\frac{\partial h_{t}}{\partial (h_{t-1})^{T}}\cdot\tanh'\cdot\frac{\partial h_{t-1}}{\partial (h_{t-2})^{T}}...\cdot\tanh'\cdot\frac{\partial h_{i+1}}{\partial (h_{i})^{T}}=\frac{\partial y_{t}}{\partial h_{t}}\cdot (tanh')^{t-i}\cdot W^{t-i}} ∂hi∂yt=∂ht∂yt⋅∂hi∂ht=∂ht∂yt⋅tanh′⋅∂(ht−1)T∂ht⋅tanh′⋅∂(ht−2)T∂ht−1...⋅tanh′⋅∂(hi)T∂hi+1=∂ht∂yt⋅(tanh′)t−i⋅Wt−i
所以最终结果是: ∂ L o s s ∂ W i h h = ∂ L o s s ∂ y t ⋅ ∂ y t ∂ h t ⋅ ( t a n h ′ ) t − i ⋅ W t − i ⋅ ( h i − 1 ) T \mathbf {\frac{\partial Loss}{\partial W_{i}^{hh}}=\frac{\partial Loss}{\partial y_{t}}\cdot\frac{\partial y_{t}}{\partial h_{t}}\cdot (tanh')^{t-i}\cdot W^{t-i}\cdot(h_{i-1})^T} ∂Wihh∂Loss=∂yt∂Loss⋅∂ht∂yt⋅(tanh′)t−i⋅Wt−i⋅(hi−1)T
可以看到涉及到矩阵W的连乘。
线性代数中有: W = P − 1 Σ P W=P^{-1}\Sigma P W=P−1ΣP
其中, E = P − 1 P E=P^{-1} P E=P−1P为单位矩阵, Σ \Sigma Σ为对角线矩阵,对角线元素为W对应的特征值。即
Σ = [ λ 1 . . . 0 . . . . . . . . . . . . . . . λ m ] \Sigma =\begin{bmatrix} \lambda _{1} & ... & 0\\ ... &... &... \\ ... & ... &\lambda _{m} \end{bmatrix} Σ=⎣⎡λ1...............0...λm⎦⎤
所以有:
W = P − 1 Σ T P = Σ = [ λ 1 T . . . 0 . . . . . . . . . . . . . . . λ m T ] W=P^{-1}\Sigma^T P=\Sigma =\begin{bmatrix} \lambda _{1}^T & ... & 0\\ ... &... &... \\ ... & ... &\lambda _{m} ^T \end{bmatrix} W=P−1ΣTP=Σ=⎣⎡λ1T...............0...λmT⎦⎤
所以有:
- 矩阵特征值 λ m \lambda _{m} λm要么大于1要么小于1。所以t时刻导数要么梯度消失,要么梯度爆炸。而且比DNN更严重。因为DNN链式求导累乘的各个W是不一样的,有的大有的小,互相还可以抵消影响。而RNN的W全都一样,必然更快的梯度消失或者爆炸。
- λ m > 1 \lambda _{m}>1 λm>1则 λ m T → ∞ \lambda _{m}^T→\infty λmT→∞,过去信息越来越强, λ m < 1 \lambda _{m}<1 λm<1则 λ m T → 0 \lambda _{m}^T→0 λmT→0,信息原来越弱,传不远。所有时刻W都相同,即所有时刻传递信息的强度都一样,传递的信息无法调整,和当前时刻输入没太大关系。
- 为了避免以上问题,序列不能太长。
- 无法解决超长依赖问题:例如 h 1 h_1 h1传到 h 10 h_{10} h10, x 1 x_1 x1的信息在中间被多个W和 x 2 − x 9 x_2-x_9 x2−x9稀释
- 递归模型,无法并行计算
二、长短时记忆网络LSTM
RNN的缺点是信息经过多个隐含层传递到输出层,会导致信息损失。更本质地,会造成网络参数难以优化。LSTM加入全局信息context,可以解决这一问题。
2.1 LSTM模型结构
1. 跨层连接
LSTM首先将隐含层更新方式改为:
u t = t a n h ( W x h x t + b x h + W h h h t − 1 + b h h ) \mathbf {u_{t}=tanh(W^{xh}x_{t}+b^{xh}+W^{hh}h_{t-1}+b^{hh})} ut=tanh(Wxhxt+bxh+Whhht−1+bhh)
h t = h t − 1 + u t \mathbf {h_{t}=h_{t-1}+u_{t}} ht=ht−1+ut
这样可以直接将 h k h_{k} hk与 h t h_{t} ht相连,实现跨层连接,减小网络层数,使得网络参数更容易被优化。证明如下:
h t = h t − 1 + u t = h t − 2 + u t − 1 + u t = . . . = h k + u k + 1 + u k + 2 + . . . + u t − 1 + u t \mathbf {h_{t}=h_{t-1}+u_{t}=h_{t-2}+u_{t-1}+u_{t}=...=h_{k}+u_{k+1}+u_{k+2}+...+u_{t-1}+u_{t}} ht=ht−1+ut=ht−2+ut−1+ut=...=hk+uk+1+uk+2+...+ut−1+ut
- 增加遗忘门 forget gate
上式直接将旧状态 h t − 1 h_{t-1} ht−1和新状态 u t u_{t} ut相加,没有考虑两种状态对 h t h_{t} ht的不同贡献。故计算 h t − 1 h_{t-1} ht−1和 u t u_{t} ut的系数,再进行加权求和
f t = σ ( W f , x h x t + b f , x h + W f , h h h t − 1 + b f , h h ) \mathbf {f_{t}=\sigma(W^{f,xh}x_{t}+b^{f,xh}+W^{f,hh}h_{t-1}+b^{f,hh})} ft=σ(Wf,xhxt+bf,xh+Wf,hhht−1+bf,hh)
h t = f t ⊙ h t − 1 + ( 1 − f t ) ⊙ u t \mathsf {h_{t}=f_{t}\odot h_{t-1}+(1-f_{t})\odot u_{t}} ht=ft⊙ht−1+(1−ft)⊙ut
其中 σ \sigma σ表示sigmoid函数,值域为(0,1)。当 f t f_{t} ft较小时,旧状态贡献也较小,甚至为0,表示遗忘不重要的信息,所以称为遗忘门。 - 增加输入门 Input gate
上一步问题是旧状态 h t − 1 h_{t-1} ht−1和新状态 u t u_{t} ut权重互斥。但是二者可能都很大或者很小。所以需要用独立的系数来调整。即:
i t = σ ( W i , x h x t + b i , x h + W i , h h h t − 1 + b i , h h ) \mathbf {i_{t}=\sigma(W^{i,xh}x_{t}+b^{i,xh}+W^{i,hh}h_{t-1}+b^{i,hh})} it=σ(Wi,xhxt+bi,xh+Wi,hhht−1+bi,hh)
h t = f t ⊙ h t − 1 + i t ⊙ u t \mathsf {h_{t}=f_{t}\odot h_{t-1}+i_{t}\odot u_{t}} ht=ft⊙ht−1+it⊙ut
i t i_{t} it用于控制输入状态 u t u_{t} ut对当前状态的贡献,所以称为输入门 - 增加输出门output gate
o t = σ ( W o , x h x t + b o , x h + W o , h h h t − 1 + b o , h h ) \mathbf {o_{t}=\sigma(W^{o,xh}x_{t}+b^{o,xh}+W^{o,hh}h_{t-1}+b^{o,hh})} ot=σ(Wo,xhxt+bo,xh+Wo,hhht−1+bo,hh) - 综合计算
u t = t a n h ( W x h x t + b x h + W h h h t − 1 + b h h ) \mathbf {u_{t}=tanh(W^{xh}x_{t}+b^{xh}+W^{hh}h_{t-1}+b^{hh})} ut=tanh(Wxhxt+bxh+Whhht−1+bhh)
f t = σ ( W f , x h x t + b f , x h + W f , h h h t − 1 + b f , h h ) \mathbf {f_{t}=\sigma(W^{f,xh}x_{t}+b^{f,xh}+W^{f,hh}h_{t-1}+b^{f,hh})} ft=σ(Wf,xhxt+bf,xh+Wf,hhht−1+bf,hh)
i t = σ ( W i , x h x t + b i , x h + W i , h h h t − 1 + b i , h h ) \mathbf {i_{t}=\sigma(W^{i,xh}x_{t}+b^{i,xh}+W^{i,hh}h_{t-1}+b^{i,hh})} it=σ(Wi,xhxt+bi,xh+Wi,hhht−1+bi,hh)
c t = f t ⊙ c t − 1 + i t ⊙ u t \mathbf {c_{t}=f_{t}\odot c_{t-1}+i_{t}\odot u_{t}} ct=ft⊙ct−1+it⊙ut
h t = o t ⊙ t a n h ( c t ) \mathbf {h_{t}=o_{t}\odot tanh(c_{t})} ht=ot⊙tanh(ct)
y n = s o f t m a x ( W h y h n + b h y ) \mathbf {y_{n}=softmax(W^{hy}h_{n}+b^{hy})} yn=softmax(Whyhn+bhy)
- 遗忘门: f t f_{t} ft,是 c t − 1 c_{t-1} ct−1的系数,可以过滤上一时刻的记忆信息。否则之前时刻的 c t c_t ct完全保留, c t c_t ct越来越大, h t = o t ⊙ t a n h ( c t ) \mathbf {h_{t}=o_{t}\odot tanh(c_{t})} ht=ot⊙tanh(ct)tanh会马上饱和,无法输入新的信息。
- 输入门: i t i_{t} it,是 u t u_{t} ut的系数,可以过滤当前时刻的输入信息。即不会完整传递当前输入信息,可以过滤噪声等
- 输出门: o t o_{t} ot,是 t a n h ( c t ) tanh(c_{t}) tanh(ct)的系数,过滤记忆信息。即 c t c_t ct一部分与当前分类有关,部分是与当前分类无关信息,只是用来传递至未来时刻
- 三个门控单元,过滤多少记住多少,都跟前一时刻隐含层输出和当前时刻输入有关
- 记忆细胞: c t c_{t} ct,记录了截止当前时刻的重要信息。
可以看出RNN的输入层隐含层和输出层三层都是共享参数,到了LSTM都变成参数不共享了。
2.2 双向循环神经网络Bi-LSTM
- 解决循环神经网络信息单向流动的问题。(比如一个词的词性与前面的词有关,也与自身及后面的词有关)
- 将同一个输入序列分别接入前向和后向两个循环神经网络中,再将两个循环神经网络的隐含层结果拼接在一起,共同接入输出层进行预测。其结构如下:

此外还可以堆叠多个双向循环神经网络。
LSTM比起RNN多了最后时刻的记忆细胞,即:
bilstm=nn.LSTM(
input_size=1024,
hidden_size=512,
batch_first=True,
num_layers=2,#堆叠层数
dropout=0.5,
bidirectional=True#双向循环)
hidden, hn = self.rnn(inputs)
#hidden是各时刻的隐含层,hn为最后时刻隐含层
hidden, (hn, cn) = self.lstm(inputs)
#hidden是各时刻的隐含层,hn, cn为最后时刻隐含层和记忆细胞
三、序列到序列模型
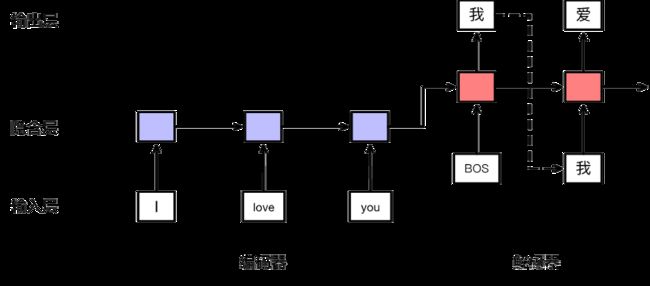
encoder最后状态的输出输入decoder作为其第一个隐含状态 h 0 h_0 h0。decoder每时刻的输出都会加入下一个时刻的输入序列,一起预测下一时刻的输出,直到预测出End结束。