KKT条件
KKT条件
-
- 1.摘要
- 2.函数优化问题
- 3.KKT条件简介
- 4.推导
- 5.例子
1.摘要
本篇博客参考了国立交通大学周志成老师的线代启示录,主要对不等式约束优化问题中KKT条件进行简要推导,以便加深理解和记忆。
2.函数优化问题
1)对于无条件极值问题,可以通过函数极值存在的必要条件寻找极值点(一阶导求驻点、二阶导数测试)
2)对于等式条件极值问题,可以通过引入拉格朗日乘子构造拉格朗日函数,将原问题等价转换为无条件极值问题
3)对于不等式条件问题,由于不等式条件对函数可行域进行了区域的分割,且区域带来了方向性约束,如果想沿着上述的思路将条件极值转为无条件极值,则需要增加更多的约束条件。这时就要用到KKT条件
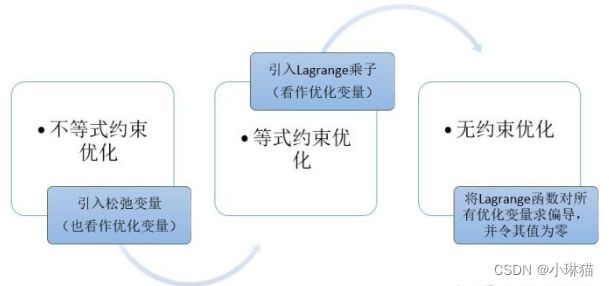
3.KKT条件简介
KKT(Karush-Kuhn-Tucker)条件是针对约束优化的通用方法,它的基础是拉格朗日条件极值,是非线性规划最佳解的必要条件。KKT条件将拉格朗日数乘法所处理的等式约束优化问题推广至不等式。在实际应用上,KKT条件(方程组)一般不存在解析解,许多优化问题可供数值计算选用。
4.推导
目标函数为: f ( X ) f(X) f(X)
不等式约束为: g ( X ) ≤ 0 g(X) ≤ 0 g(X)≤0 注意应将不等式写成小于0的形式
引入松弛变量的新目标函数为: L ( X , λ ) = f ( X ) + λ g ( X ) L(X,λ) = f(X) + λg(X) L(X,λ)=f(X)+λg(X)
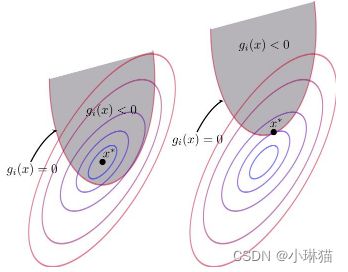
1)互斥松弛性
- 情况一:最优解处于约束条件内部,这时约束条件是无效的,约束优化问题退化为无约束优化问题,可以将引入的松弛变量λ写为0
- 情况二:最优解处于约束条件边界上,这时约束优化是有效的,不等式约束问题退化为等式约束问题,可以将约束条件去除不等号,即 g ( X ) = 0 g(X) = 0 g(X)=0
综合上述两种情况可知,无论最优解的位置如何,都满足: λ g ( X ) = 0 λg(X)=0 λg(X)=0,这称为互斥松弛性
2)对偶可行性
对于上述的情况一,约束条件无需考虑,对于情况二还需要考虑原目标函数与不等式约束函数梯度方向的关系问题,这是因为不等式约束相比于等式约束中,虽然都是在约束边界上进行考虑,但是不等式约束中最佳值的位置是确定的,在约束条件外部,但等式约束中最佳值的位置是不定的,可能在约束边界的任意一侧。
- 因为最佳值在约束条件外部,因而原目标函数 f ( X ) f(X) f(X)的梯度指向了约束条件内部;
- 因为不等式约束函数在约束条件中是小于0的,在约束条件外部是大于0的,因而不等式约束函数 g ( X ) g(X) g(X)在约束边界上的梯度指向了大于0的区域,即约束函数的外部。(这里可能会想为什么说约束函数在约束边界两侧是异号的,梯度就指向大于0的一侧?约束函数在小于0的一侧函数值不也可能上升么?这里需要注意梯度是指函数上升速度最快方向上的偏导向量,例如:相同单位长度的变换,相较于-2在约束边界内增至-1,当然没有从-2增至0的上升速度快,因而梯度是指向约束条件外部)
综合上述两点可知,在条件边界上目标函数 f ( X ) f(X) f(X)与不等式约束函数 g ( X ) g(X) g(X)的梯度方向是相反的。
通过令新的目标函数L(X,λ)对X的梯度等于0可得: L ( X , λ ) X = ▽ f ( X ) + λ ▽ g ( X ) = 0 L(X,λ)_X = ▽ f(X) + λ ▽g(X) = 0 L(X,λ)X=▽f(X)+λ▽g(X)=0,可得等式: ▽ f ( X ) = − λ ▽ g ( X ) ▽ f(X) = -λ ▽g(X) ▽f(X)=−λ▽g(X)
由于上述推导得: ▽ f ( X ) ▽ g ( X ) < 0 ▽ f(X)▽g(X) <0 ▽f(X)▽g(X)<0,所以 λ ≥ 0 λ ≥ 0 λ≥0
3)综合上述两个额外的条件,再加上引入松弛变量后的新目标函数对X和λ的梯度为0,以及原不等式的约束条件我们便得到了KKT条件方程组。
∇ x L = 0 g ( x ) ≤ 0 λ ≥ 0 λ g ( x ) = 0 ∇_x L = 0 \\ g(x) ≤ 0 \\ λ ≥0 \\ λg(x) = 0 \\ ∇xL=0g(x)≤0λ≥0λg(x)=0
4)在上述推导的过程中,为了方便起见,我们仅引入了一个不等式约束条件,且没有引入任何等式约束条件。在实际的求解过程中,不等式约束条件和等式约束条件是都可以参与运算且可以有多个的,这里给出一个完整的形式。
目标函数: a r g m i n f ( x ) argmin\;\;f(x) argminf(x)
等式约束: g i ( x ) = 0 , i = 1 , . . . , m g_i(x) = 0,\;i=1,...,m gi(x)=0,i=1,...,m
不等式约束: h j ( x ) ≤ 0 , j = 1 , . . . , n h_j(x) ≤ 0,\;j=1,...,n hj(x)≤0,j=1,...,n
构造Lagrangian 函数: L ( x , λ i , u j ) = f ( x ) + ∑ i = 1 m λ i g i ( x ) + ∑ j = 1 n u j h k ( x ) L(x,{λ_i},{u_j}) = f(x) + \sum_{i=1}^m λ_ig_i(x) + \sum_{j=1}^n u_jh_k(x) L(x,λi,uj)=f(x)+∑i=1mλigi(x)+∑j=1nujhk(x)
KKT条件:
∇ x L = 0 g i ( x ) = 0 , i = 1 , . . . , m h j ( x ) ≤ 0 , j = 1 , . . . , n u j ≥ 0 , j = 1 , . . . , n u j h j ( x ) = 0 , j = 1 , . . . , n ∇_x L = 0 \\ g_i(x) = 0,i=1,...,m \\ h_j(x) ≤ 0 ,j=1,...,n \\ u_j ≥0 ,j=1,...,n \\ u_jh_j(x)=0 ,j=1,...,n \\ ∇xL=0gi(x)=0,i=1,...,mhj(x)≤0,j=1,...,nuj≥0,j=1,...,nujhj(x)=0,j=1,...,n
5.例子
这里给出一个简单示例。
设目标函数为: f ( X ) = f ( x 1 , x 2 ) = x 1 2 + x 2 2 f(X)=f(x_1,x_2) = x_1^2 + x_2^2 f(X)=f(x1,x2)=x12+x22
设不等式约束条件为: x 2 < = a x_2 <=a x2<=a,由此可得不等式约束函数为: g ( X ) = g ( x 1 , x 2 ) = x 2 − a g(X) = g(x_1,x_2) = x_2 -a g(X)=g(x1,x2)=x2−a
设引入松弛变量的拉格朗日函数为: L ( X , λ ) = f ( X ) + λ g ( X ) = x 1 2 + x 2 2 + λ ( x 2 − a ) L(X,λ) = f(X) + λg(X) = x_1^2 + x_2^2 + λ(x_2 -a) L(X,λ)=f(X)+λg(X)=x12+x22+λ(x2−a)
KKT条件为:
L ( X , λ ) x 1 = 2 x 1 = 0 L ( X , λ ) x 2 = 2 x 2 + λ = 0 x 2 ≤ a λ > = 0 λ ( x 2 − a ) = 0 L(X,λ)_{x_1} = 2x_1 = 0 \\ L(X,λ)_{x_2} = 2x_2 + λ = 0 \\ x_2 ≤ a \\ λ >= 0 \\ λ(x_2-a) = 0 L(X,λ)x1=2x1=0L(X,λ)x2=2x2+λ=0x2≤aλ>=0λ(x2−a)=0
解得:
x 1 = 0 x 2 = − 1 2 λ x 2 ≤ a λ > = 0 λ ( x 2 − a ) = 0 x_1 = 0 \\ x_2 = - \frac 1 2 λ \\ x_2 ≤ a \\ λ >= 0 \\ λ(x_2-a) = 0 x1=0x2=−21λx2≤aλ>=0λ(x2−a)=0
①设λ=0,得:
x 1 = 0 x 2 = − 1 2 λ = 0 a ≥ x 2 ≥ 0 λ = 0 x_1 = 0 \\ x_2 = - \frac 1 2 λ = 0 \\ a ≥ x_2 ≥ 0 \\ λ = 0 \\ x1=0x2=−21λ=0a≥x2≥0λ=0
②设 x 2 = a x_2 = a x2=a,得:
x 1 = 0 x 2 = a λ = − 2 x 2 = − 2 a λ = − 2 a ≥ 0 得, a ≤ 0 x_1 = 0 \\ x_2 = a \\ λ = -2x_2 = -2a \\ λ = -2a ≥ 0 \;\;得,a≤0 \\ x1=0x2=aλ=−2x2=−2aλ=−2a≥0得,a≤0
综上①②得:
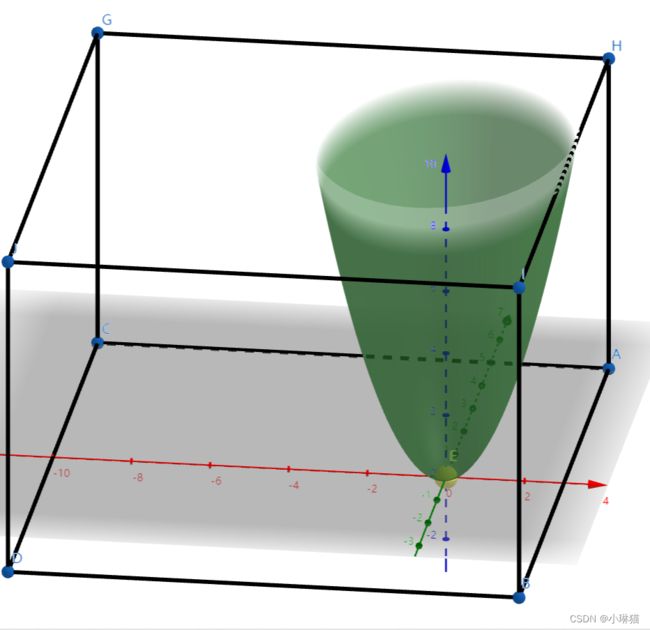
① a≥0时, X = (0,0)
由下图可以看出,当a≥0时,函数的极值点在约束条件内,所以约束条件失效,极小值在椭圆抛物面的顶点处(黄色点)
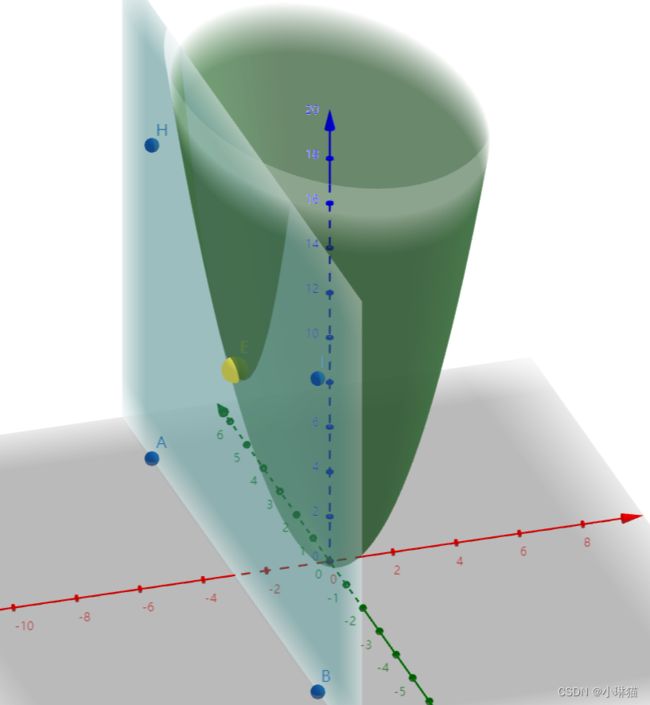
② a<0时,X=(0,a)
由下图可以看出,当a≤0时,函数的极值点不在约束条件内,约束条件有效,约束在边界上,极小值X在边界上(0,a)处取(黄色点)