IR

IR，也就是中间代码（Intermediate Representation，有时也称 Intermediate Code，IC），它是编译器中很重要的一种数据结构。编译器在做完前端工作以后，首先就是生成 IR，并在此基础上执行各种优化算法，最后再生成目标代码。

 

通常情况下，IR 有两种用途，一种是用来做分析和变换的，一种是直接用于解释执行的。

编译器中，基于 IR 的分析和处理工作，一开始可以基于一些抽象层次比较高的语义，这时所需要的 IR 更接近源代码。而在后面，则会使用低层次的、更加接近目标代码的语义。

 

基于这种从高到低的抽象层次，IR 可以归结为 HIR、MIR 和 LIR 三类。

HIR：基于源语言做一些分析和变换

假设你要开发一款 IDE，那最主要的功能包括：发现语法错误、分析符号之间的依赖关系（以便进行跳转、判断方法的重载等）、根据需要自动生成或修改一些代码（提供重构能力）。这个时候，你对 IR 的需求，是能够准确表达源语言的语义就行了。这种类型的 IR，可以叫做 High IR，简称 HIR。

 

其实，AST 和符号表就可以满足这个需求。也就是说，AST 也可以算作一种 IR。如果你要开发 IDE、代码翻译工具（从一门语言翻译到另一门语言）、代码生成工具、代码统计工具等，使用 AST（加上符号表）就够了。

 

当然，有些 HIR 并不是树状结构（比如可以采用线性结构），但一般会保留诸如条件判断、循环、数组等抽象层次比较高的语法结构。基于 HIR，可以做一些高层次的代码优化，比如常数折叠、内联等。在 Java 和 Go 的编译器中，你可以看到不少基于 AST 做的优化工作。

 

MIR：独立于源语言和 CPU 架构做分析和优化

大量的优化算法是可以通用的，没有必要依赖源语言的语法和语义，也没有必要依赖具体的 CPU 架构。这些优化包括部分算术优化、常量和变量传播、死代码删除等，实现这类分析和优化功能的 IR 可以叫做 Middle IR，简称 MIR。

因为 MIR 跟源代码和目标代码都无关，所以在讲解优化算法时，通常是基于 MIR，比如三地址代码（Three Address Code，TAC）。

TAC 的特点是，最多有三个地址（也就是变量），其中赋值符号的左边是用来写入的，而右边最多可以有两个地址和一个操作符，用于读取数据并计算。

 

LIR：依赖于 CPU 架构做优化和代码生成

是它的指令通常可以与机器指令一一对应，比较容易翻译成机器指令（或汇编代码）。因为 LIR 体现了 CPU 架构的底层特征，因此可以做一些与具体 CPU 架构相关的优化。

 

鲸书（Advanced Compiler Design and Implementation）

其实，在一个编译器里，有时候会使用抽象层次从高到低的多种 IR，从便于“人”理解到便于“机器”理解。

 

 

P-code：用于解释执行的 IR

这类 IR 还有一个名称，叫做 P-code，也就是 Portable Code 的意思。由于它与具体机器无关，因此可以很容易地运行在多种电脑上。这类 IR 对编译器来说，就是做编译的目标代码。

Java 的字节码就是这种 IR。除此之外，Python、Erlang 也有自己的字节码，.NET 平台、Visual Basic 程序也不例外。

 

其实，你也完全可以基于 AST 实现一个全功能的解释器，只不过性能会差一些。对于专门用来解释执行 IR，通常会有一些特别的设计，跟虚拟机配合来尽量提升运行速度。

P-code 也可能被进一步编译，形成可以直接执行的机器码。Java 的字节码就是这样的例子。

 

 

其实 IR 通常是没有书写格式的。一方面，大多数的 IR 跟 AST 一样，只是编译过程中的一个数据结构而已，或者说只有内存格式。比如，LLVM 的 IR 在内存里是一些对象和接口。

 

在少量情况下，IR 有比较严格的输出格式，不仅用于显示和分析，还可以作为结果保存，并可以重新读入编译器中。比如，LLVM 的 bitcode，可以保存成文本和二进制两种格式，这两种格式间还可以相互转换。

 

 

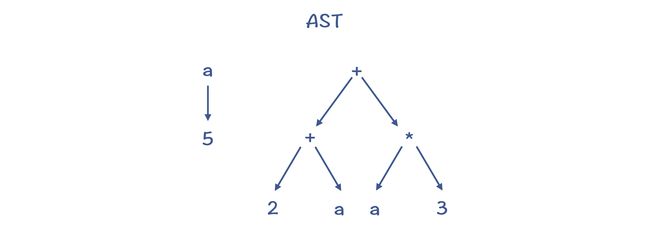
在实际的实现中，有线性结构、树结构、有向无环图（DAG）、程序依赖图（PDG）等多种格式。

 

树结构的缺点是，可能有冗余的子树

 

编译器会根据需要，选择合适的数据结构。在运行某些算法的时候，采用某个数据结构可能会更顺畅，而采用另一些结构可能会带来内在的阻滞。所以，我们一定要根据具体要处理的工作的特点，来选择合适的数据结构。

 

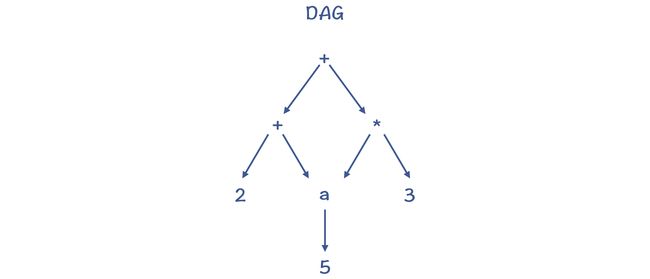
有向无环图（Directed Acyclic Graph，DAG）DAG 结构，是在树结构的基础上，消除了冗余的子树。比如，上面的例子转化成 DAG 以后，对 a 的内存访问只做一次就行了

 

在 LLVM 的目标代码生成环节，就使用了 DAG 来表示基本块内的代码。

 

程序依赖图（Program Dependence Graph，PDG）

程序依赖图，是显式地把程序中的数据依赖和控制依赖表示出来，形成一个图状的数据结构。基于这个数据结构，我们再做一些优化算法的时候，会更容易实现。

有很多编译器在运行优化算法的时候，都基于类似 PDG 的数据结构，比如我在课程后面会分析的 Java 的 JIT 编译器和 JavaScript 的编译器。

PDG这种数据结构里，因为会有很多图节点，又被形象地称为“节点之海（Sea of Nodes）”。

 

一个重要的 IR 设计范式：SSA 格式。SSA 是 Static Single Assignment 的缩写，也就是静态单赋值。这是 IR 的一种设计范式，它要求一个变量只能被赋值一次。

 

“y = x1 + x2 + x3 + x4”的普通 TAC 如下：

y := x1 + x2;
y := y + x3;
y := y + x4;

 

y 被赋值了三次，如果我们写成 SSA 的形式，

t1 := x1 + x2;
t2 := t1 + x3;
y  := t2 + x4; 

为什么要费力写成这种形式？

使用 SSA 的形式，体现了精确的“使用 - 定义（use-def）”关系。并且由于变量的值定义出来以后就不再变化，使得基于 SSA 更容易运行一些优化算法。

BB1:
  b1 := 0
  if a>10 goto BB3
BB2:
  b2 := 10
  goto BB4
BB3:
  b3 := a
BB4:
  b4 := phi(BB2, BB3, b2, b3)
  return b4

phi 指令，会根据控制流的实际情况确定 b4 的值。如果 BB4 的前序节点是 BB2，那么 b4 的取值是 b2；而如果 BB4 的前序节点是 BB3，那么 b4 的取值就是 b3。

如果要满足 SSA 的要求，也就是一个变量只能赋值一次，那么在遇到有程序分支的情况下，就必须引入 phi 指令。

 

SSA 格式的优点，现代语言用于优化的 IR，很多都是基于 SSA 的了。例如：Java 的 JIT 编译器、JavaScript 的 V8 编译器、Go 语言的 gc 编译器、Julia 编译器，以及 LLVM 工具等,都是基于 SSA。

 

 

整个编译过程，就是生成从高抽象度到低抽象度的一系列 IR，以及发生在这些 IR 上的分析与处理过程。