TFE:一种用于深度学习的多阶段Python嵌入式DSL
TensorFlow Eager: A Multi-stage, Python-embedded DSL For Machine Learning
介绍和相关工作
在编程语言的观点下,DSL 可以分为命令式(Imperative)和声明式(Declarative)两种。使用命令式 DSL 编写可微分程序(基于现有自动微分软件编写的模型)就像使用命令式编程语言(比如 Python),它的性能瓶颈受制于解释器(Interpreter),并且模型的串行化比较困难。为了解决这个问题,声明式 DSL 把模型的执行与模型的定义分离,这类先定义后执行(Define-before-run)的运行库要求用户将模型划分为数据流图(Dataflow graph)的各个阶段(Stage),使得编译器优化和并行处理成为可能,从而简化部署、分布式和代码生成;但是,这也导致用户不能随意使用宿主语言的特性,而 DSL 的学习过程通常有陡峭的学习曲线;对于存在数据依赖的结构(比如控制流),这类 DSL 无法合适地描述。
理想的 DSL 应当同时具有命令式的灵活性和声明式的高效性,于是本文提出了 TensorFlow Eager。它是 TensorFlow 的一个可选扩展,只需要在程序开始时执行 tf.enable_eager_execution() 即可。TFE 默认是以命令式执行的,它另外提供了 Python 装饰器(Decorator)来追踪计算图的上下文,将建立计算图的原语操作(Primitive operations)和归属的输入输出阶段化(Staging),返回可执行的图函数(Graph function)。图函数和命令式代码共享同一个词法环境(Lexical environment),包括原语操作、计算核心和用户可见的 API 等。
在 TFE 中,用户必须手动对计算进行阶段化,可能会导致代码的重构。理想的可微分程序框架应当不需要用户干预就可以自动阶段化。一种方法(DLVM, Swift for TensorFlow, and Zygote)是将框架嵌入到预先编译好的过程式语言,把计算图提取和自动微分实现为编译器重写,但是 Python 的灵活性让 DSL 的嵌入困难重重。一些项目(AutoGraph)在 Python 的 AST 上对命令式代码进行重写,产生计算图,该技术不在本文的讨论范围内。另一种阶段化计算的选择(NVIDIA CuDNN)是融合计算核心(Fused kernel),虽然效果显著,但是泛用性差。
TFE 不是第一个提出多阶段编程模型(Multi-stage programming model)的 Python 库。JAX 是一种基于 XLA 的、为异构设备提供代码生成的 tracing-JIT 编译器,它提出了与本文类似的编程范式。MXNet 和 Gluon 也尝试在命令式计算和阶段化计算中间做插值,但抽象的视角比本文的更高。PyTorch 实现的 staging tracer 与本文的接近。可微分编程之外,Terra(基于 Lua 嵌入的 DSL)对多阶段编程的处理比本文更公式化;OptiML(基于 Scala 嵌入的 DSL)也支持阶段化,但是不支持自动微分。DSL 之外,支持 JIT 编译的还有 Numba 和 PyPy 等。
多阶段编程涉及阶段化变换(Staging transformation)和部分评估(Partial Evaluation)。
设计理念
用户编写 Python 程序的经验应当可以轻易地迁移到 TFE 的使用上,从小规模测试到在异构设备上部署模型推导的路径也需要尽可能平滑。为此,TFE 提出了三条设计原则:
- 特权下的命令式执行(Privilege imperative execution)。由于 Python 是命令式的,TFE 默认也是命令式执行的,阶段化执行是可选的,而且通常是不必要的。
- 对 Python 的无缝嵌入(Seamlessly embed into Python)。编写 TensorFlow 程序锻炼的是元编程(Metaprogramming)能力,而命令式执行让用户能够编写像宿主语言一样的程序(Pythonic),包含原生的控制流、递归、数据结构,甚至是
pdb断点调试。 - 阶段化命令式代码为数据流图(Stage imperative code as dataflow graphs)。
执行模型(Execution Model)
多阶段编程
TFE 提供了两种执行算子的方式:命令式或者作为静态图的一部分。
- 命令式执行:默认,构造算子、立即执行。
- 阶段化执行:到 Python 解释器之间来回往返的开销制约了命令式执行的性能,阶段化执行不仅解除了这个限制,还能额外进行算子间并行(Inter-op parallelism)、常量折叠、缓存重用等优化。
TFE 提供了装饰器 function 来记录算子和张量流,遗憾的是,只支持 TensorFlow 中的操作,而不是任意的 Python 代码。调用装饰器返回的 Callable,就会执行装饰器产生的计算图,而不是原来的 Python 代码。计算图的运行时环境使用 C++ 编写,它会自动划分子图,分配给可用设备并尽可能尝试并行化。function 装饰器还支持基于 XLA 的代码生成,用以在 TPU 上运行。
需要注意的是,function 装饰器是 JIT tracer,在计算图上下文中(非 TensorFlow 的 Python 代码原样执行),运算返回的是计算结果的符号表示,而不是具体的值。
@tf.contrib.eager.function
def add_noise():
eye = tf.eye(5)
randn = np.random.randn(5, 5)
return eye + randn
一般情况下,每次调用 add_noise() 会返回不同的结果,但是使用装饰器以后,每次调用都会产生相同的返回值,因为 add_noise() 的上下文(比如随机化种子)以常量形式记录下来了。作为推论,如果一个函数存在副作用(比如引用了一个全局自增变量),使用 function 装饰器会破坏语义等价性。
此外,由于装饰器基于 tracing 技术而不是基于源代码的分析,Python 循环是被完全展开的,这样可能会导致计算图过大,所以需要使用 TensorFlow 的控制流(tf.cond、tf.while_loops)来代替 Python 的控制流,产生更小粒度的控制流。
自动微分与串行化
x = tf.constant(3.0)
with tf.GradientTape() as t1:
with tf.GradientTape() as t2:
t1.watch(x)
t2.watch(x)
y = x * x
dy_dx = t2.gradient(y, x) # 6.0
d2y_dx2 = t1.gradient(dy_dx, x) # 2.0
TFE 提供了 Tape 来监视变量,如果有运算以这个变量为输入,Tape 就会记录下对应的运算,用于后面进行反向模式自动微分(Reverse-mode automatic differentiation)。多个 Tape 可以同时激活,还支持互相嵌套。
x = tf.Variable(3.0)
with tf.GradientTape() as t1:
with tf.GradientTape() as t2:
y = x * x
dy_dx = t2.gradient(y, x) # 6.0
d2y_dx2 = t1.gradient(dy_dx, x) # 2.0
TFE 和 TensorFlow 一样使用 Variable 来保存程序状态,但是 Tape 可以自动监视它们。
TFE 的 Variable 与 Python 的 Object 相对应,TensorFlow 根据创建变量的顺序为每个变量赋予唯一的标识符,如果创建了模型的两份拷贝,恢复模型权重时的顺序应当一致。为此,TFE 使用的是在 DAG 上的贪心匹配。
class Net(tf.keras.Model):
def __init__(self):
super(Net, self).__init__()
self.v = tf.Variable(1.)
self.out = tf.layers.Dense(1)
def call(self, x):
return self.out(tf.nn.softplus(x * self.v))
阶段化使得串行化不需要 Python 解释器也可以进行(每个阶段分别串行化)。
设备与分布式
a = tf.constant(1.0) # stored on CPU
b = a.gpu() # stored on GPU
TFE 使用 device 作为上下文管理器:
# stored on CPU
a = tf.constant(1.0)
b = tf.constant(2.0)
with tf.device("/gpu:0"):
c = tf.add(a, b)
assert c.numpy() == 3.0
TFE 的分布式以主程序为中心服务器,远端有若干工作服务器,每个工作服务器将各自的空闲设备上报给设备池,分发时以 /job:training/task:2/device:CPU:0 的形式命名。如果服务器属于一个集群,还可以用域名或者 IP 地址映射的方式指名。
阶段化计算
- 多态(Polymorphism)。与 Python 函数相反,图函数不存在多态(入参个数固定)。TFE 实现了一个 trace cache 来填平语义鸿沟:cache miss 会触发一次针对给定输入的 trace;cache hit 则是对已有图函数的重用。 从某种意义上说,
function装饰器提供了特殊的多态。此外,得益于绑定时刻分析(Binding-time analysis),TFE 还支持参数化计算:
@tf.contrib.eager.function
def lossy_matmul(W, x, training=True):
outputs = tf.matmul(W, x)
if training:
outputs = tf.nn.dropout(outputs, 0.2)
return outputs
W = tf.random_normal((3, 5))
x = tf.random_normal((5, 1))
# Executes a graph with dropout.
lossy_outputs = lossy_matmul(W, x, training=True)
# Executes a graph without dropout.
exact_outputs = lossy_matmul(W, x, training=False)
- 词法闭包(Lexical Closure)。并且,变量是以引用方式而不是值方式捕获的:
v = tf.Variable(0.0)
@tf.contrib.eager.function
def mutate():
v.assign_add(1.0)
return v.read_value()
mutate()
assert float(v.read_value()) == 1.0
v.assign_add(1.0)
assert float(v.read_value()) == 2.0
mutate()
assert float(v.read_value()) == 3.0
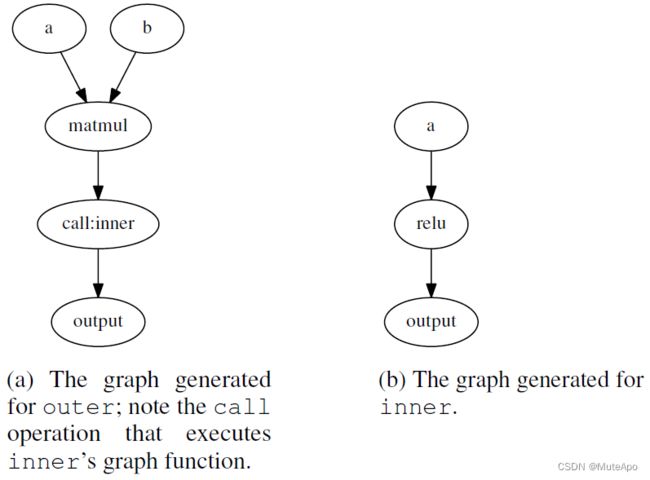
- 组装(Composition)。图函数能够以函数调用的方式组装起来:
@tf.contrib.eager.function
def inner(a):
return tf.nn.relu(a)
@tf.contrib.eager.function
def outer(a, b):
return inner(tf.matmul(a, b))
outer(tf.eye(3), tf.diag([-1.0, 1.0, 2.0]))
- 状态创建(State Creation)。用 Python 写 DL 程序的惯例是在首次调用时初始化变量,所以 TFE 的状态(比如 TensorFlow 的 Variable)能也只能在被装饰的函数首次被调用时创建,在后续的调用中装饰器就可以追踪函数行为。
转义阶段化计算(Escaping Staged Computations)
在图函数中嵌入命令式代码,有三种选择:
- 代码重构,让命令式代码之前和之后的部分可以阶段化。
- 放弃阶段化,整段维持命令式。
- 用
py_func包裹,把 Python 函数作为参数传入,在阶段化上下文中依然可以命令式执行。
py_func 能在 Tape 下执行,所以保持了可微分性质。它在命令式计算下时无效的,只有在阶段化计算中有效。py_func 也被认为是替代 C++ 使用 Python 实现自定义运算的一种快速方式。但是,py_func 把控制权交还给了单线程的 Python 解释器(性能下降),而且通常不可以串行化。
此外,TFE 提供了额外的上下文管理器 tf.init_scope,它能够暂停 trace,临时进入到命令式执行上下文。
参考资料
A. Agrawal, A, N. Modi, A. Passos, et al. TensorFlow Eager: A Multi-stage, Python-embedded DSL For Machine Learning. https://arxiv.org/abs/1903.01855