算法-二分查找

二分查找

猜数游戏的策略——二分查找

一个优秀的例子

从数字1开始慢慢地一个一个地问实在是比较笨，我们不难想到一些方法：询问100、200、300、400……来确定答案位于哪个区间内，然后在这个区间内故技重施（假设答案在300和400之间），询问310、320、330、340……来缩小这个区间。当这个区间足够小的时候，我们再对区间中的每个数字挨个询问。

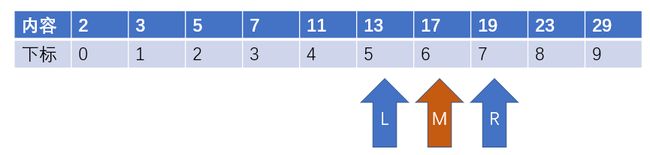
实际上，每次询问当前区间的中点是最优的策略。我们根据主持人的回答来确定最终答案是位于哪半边区间里面。由于我们每次会把当前区间的长度大约除以2，因此我们在大约10次询问之后，就一定能知道最终答案。下面这个游戏记录就展示了这个策略。

如何用程序语言描述这样一个策略？为什么这种策略是最好的呢？请先思考思考~

通用的游戏策略

用伪代码描述这样一个策略，就是下面这段：

int L = 区间左端点;
int R = 区间右端点; // 闭区间
while( L < R ) { // 区间内有至少两个数字
    int M = L+(R-L)/2; // 区间中点
    if( M是答案 ) 答对啦;
    else if( M比答案小 ) L = M+1;
    else R = M-1; // M比答案大
}
// 若运行到这里，因为答案一定存在，所以一定有L==R，且L是答案

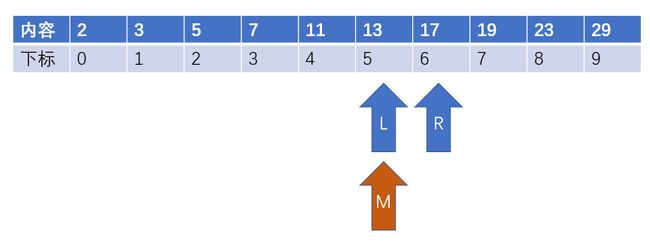
这也是所谓二分查找的思路：我们设定一个初始的L和R，保证答案在[L,R]中，当[L,R]中不止有一个数字的时候，取区间的中点M，询问这个中点和答案的关系，来判断答案是M，还是位于[L,M-1]中，还是位于[M+1,R]中。

这里有一个二分查找的可视化过程，你可以进入网站体验一下二分查找的步骤过程。

虽然二分查找的方法能够帮助我们快速找到答案，但我们还有很多很多的细节问题没有处理，比如：

• 如果循环最后因为不满足L < R条件而退出，这时候L和R到底是什么关系？答案是什么？
• 如果答案不存在会怎么样？

我们暂时并不需要考虑这些问题，因为我们现在的目标是“理解二分查找的思路，并学会手算二分查找”。既然是手算，那么当区间内剩余的数字个数寥寥无几的时候，我们只要挨个询问一遍就行了，这并不影响二分查找的复杂度。

为什么要用这种策略？

为什么二分查找的方法是最优的呢？

回顾我们刚刚讲到的“最优”的定义：在最差的情况下，我们进行询问的次数最少。

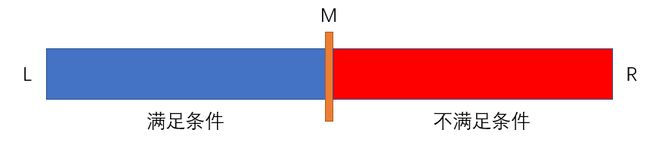
而这个猜数游戏的本质是什么？我们每进行一次询问，就可以排除一些错误答案。

如图，当我们询问M位置的时候，主持人告诉我们的信息实际上帮助我们排除了一部分错误答案，从而缩小正确答案所在的区间长度。

因此，在最差的情况下，如果我们询问的位置不是区间的中点，那么主持人帮我们排除掉的区间一定是长度较短的那部分。

所以，只有当我们询问区间中点的时候，我们才能让可行区间的长度以最快的速度变短——每次大约变为原来长度的一半，所以二分查找的时间复杂度是$lo{g}_2(n)$。

二分查找时间复杂度的计算方法：

比如，在猜数字的游戏中，假设我们一开始有n个数字。每次把剩余数字的区间分成两半，直到x次后只剩下最后一个数字，就是我们想要的答案啦。 计算公式如下：

$n\ast 1/(2^x)=1$

x次后只剩下最后一个数字

$x=lo{g}_2(n)$
那么，x的值就是log n咯

这就是为什么二分查找方法是最快的方法。

数组上的二分查找

现在，让我们从游戏回到编程问题。

首先，来看一个二分查找问题的最经典的应用：

你有一个长度为n的排好序的数组a，你需要在$lo{g}_2(n)$ 的时间复杂度内求出数组a中第一个大于等于x的元素是多少，或者输出“数组a中不存在大于等于x的元素”。

我们现在并不要求写出通用代码，只要会手算二分查找即可，因此我们用下面这个数组作为例子，一步一步地来看看二分查找算法是如何运行的。

因为数组是排好序的，所以我们可以直接根据最后一个数来判断“数组中是否存在大于等于x的元素”。现在我们假设x = 12，需要在下面这个数组中用二分查找法找到第一个大于等于12的元素。

1、最开始有L = 0, R = 9, M = 4，我们检查a[M]和12的关系，发现a[M] < 12，因此符合条件的数字一定在a[M+1]到a[R]这些数中，所以令L = M+1，继续进行二分查找。

2、现在有L = 5, R = 9, M = 7，我们发现a[M] >= 12，因此符合条件的数字一定在a[L]到a[M]这些数字中，所以令R = M（注意不是R = M-1），继续进行二分查找。

那么，这里为什么令R = M而不是R = M-1呢？ 这是因为a[M]也可能是答案，因为我们要找的是第一个大于等于12的数字，所以a[M]不能被排除在外。

3、现在有L = 5, R = 7, M = 6，我们重复刚才的步骤，发现a[M] >= 12，于是令R = M，继续进行二分查找。

4、此时有L = 5, R = 6, M = 5，我们发现a[M] >= 12，于是继续令R = M。

5、最后，这时候已经有L = R了，这意味着a[L] = 13就是我们要找的答案咯。

总结

现在我们来看一下二分查找这个神奇的算法：

• 二分查找的原理：每次排除掉一半答案，使可能的答案区间快速缩小。
• 二分查找的时间复杂度：$lo{g}_2(n)$ ，因为每次询问会使可行区间的长度变为原来的一半。
• 我们再来看一下二分查找的思路：我们设定一个初始的L和R，保证答案在[L,R]中，当[L,R]中不止有一个数字的时候，取区间的中点M，询问这个中点和答案的关系，来判断答案是M，还是位于[L,M-1]中，还是位于[M+1,R]中。二分查找的伪代码如下：

int L = 区间左端点;
int R = 区间右端点; // 闭区间
while( L < R ) { // 区间内有至少两个数字
    int M = L+(R-L)/2; // 区间中点
    if( M是答案 ) 答对啦;
    else if( M比答案小 ) L = M+1;
    else R = M-1; // M比答案大
}
// 若运行到这里，因为答案一定存在，所以一定有L==R，且L是答案

正如之前说的，二分查找中其实还有很多细节问题没有处理，比如：

• 如果循环最后因为不满足L < R条件而退出，这时候L和R到底是什么关系？答案是什么？
• 如果答案不存在会怎么样？

代码讲解

我们先来回顾一下二分查找的思路：我们设定一个初始的L和R，保证答案在[L,R]中，当[L,R]中不止有一个数字的时候，取区间的中点M，询问这个中点和答案的关系，来判断答案是M，还是位于[L,M-1]中，还是位于[M+1,R]中。一般二分查找的伪代码如下：

int L = 区间左端点;
int R = 区间右端点;            // 闭区间
while( L < R ) {             // 区间内有至少两个数字
    int M = L + (R - L) / 2; // 求出区间中点
    if( M是答案 ) 答对啦;
    else if( M比答案小 ) L = M+1;
    else R = M-1;            // M比答案大
}
// 若运行到这里，因为答案一定存在，所以一定有L==R，且L是答案

数组上的二分查找

在一个排好序的数组上找到第一个大于等于x的数字的位置（假设数组是从小到大排好序的）。

问题： 输入n，x，以及一个长度为n的数组a（已经从小到大排好序了）

输出数组a中最左边的大于等于x的数字的下标，数组下标从0开始

输入数字都是1000000000以内的非负整数。数组长度不超过50000。若数组中不存在大于等于x的数字，输出-1

比如你要在下面这个数组中找到第一个大于等于12的数字的位置，用二分查找应该怎么做呢？请先思考一下再进入下一步～

在升序的数组上进行二分查找

在一个排好序的数组上二分查找一个数字x，一般都可以变成如下的问题：在数组中找到第一个大于等于x的数字的位置（假设数组是从小到大排好序的）。

问题： 输入n，x，以及一个长度为n的数组a（已经从小到大排好序了）

输出数组a中最左边的大于等于x的数字的下标，数组下标从0开始

输入数字都是1000000000以内的非负整数。数组长度不超过50000。若数组中不存在大于等于x的数字，输出-1

首先，我们先来运行看看在升序的数组上进行二分查找算法的代码：

请运行右侧代码，填入不同输入观察一下上述问题的答案。特别注意输入格式：

输入样例：

9 4

2 3 3 3 3 4 4 4 4

#include 
using namespace std;

int n, x, a[100000];

int main() {
    cin >> n >> x;
    // 输入数组
    for( int i = 0; i < n; ++i ) 
        cin >> a[i];
    // 考虑数组中不存在大于等于x的数字的情况
    if( x > a[n-1] ) {           
        cout << -1 << endl;
        return 0;
    }
    
    // 二分查找
    int L = 0, R = n-1;          // 数组下标从0到n-1，闭区间
    while( L < R ) {             // 当区间中至少有两个数字的时候，需要继续二分
        int M = L + (R - L) / 2; // 求出区间中点
        if( a[M] < x ) {         // 答案一定出现在[M+1,R]中
            L = M+1;
        } else {                 // a[M] >= x，答案一定出现在[L,M]中
            R = M;
        }
    }
    
    // 此时L == R，a[L]就是第一个大于等于x的数字
    if ( a[L] == x) {
        cout << L << endl;  // 如果答案存在，则输出答案
    } else {
        cout << -1 << endl; // 如果答案不存在，则输出-1
    }
    
    return 0;
}

在一个排好序的数组上找到第一个大于等于x的数字的位置（假设数组是从小到大排好序的）。

问题： 输入n，x，以及一个长度为n的数组a（已经从小到大排好序了）

输出数组a中最左边的大于等于x的数字的下标，数组下标从0开始

输入数字都是1000000000以内的非负整数。数组长度不超过50000。若数组中不存在大于等于x的数字，输出-1

首先，我们来看看在升序的数组上进行二分查找算法的伪代码：

int L = 0;
int R = n-1;                // 数组下标从0到n-1，闭区间
while( L < R ) {            // 区间内有至少两个数字
    int M = L+(R-L)/2;      // 求出区间中点
    if( M比答案小 ) L = M+1; // 答案一定出现在[M+1,R]中
    else R = M;             // a[M] >= x，答案一定出现在[L,M]中
}
// 此时L == R，a[L]就是第一个大于等于x的数字

一些特殊情况

问题： 输入n，x，以及一个长度为n的数组a（已经从小到大排好序了）

输出数组a中最左边的大于等于x的数字的下标，数组下标从0开始

输入数字都是1000000000以内的非负整数。数组长度不超过50000。若数组中不存在大于等于x的数字，输出-1

请运行或修改这段代码在不同数组上的运行过程，输入不同x，体会一下这段代码是如何处理一些边界情况的。

• 比如：答案不存在的情况我们是如何处理的？
• 比如：当区间内只有两个数字的时候，这段代码还能正常运行吗？
• 比如：数组中有很多个重复元素的时候，这段代码还能正常运行吗？
• 比如：为什么循环结束之后一定有L == R？为什么不会出现L > R的情况？

请自己写一些简单情况出来，并手动模拟运行这段代码，想一想为什么这段代码不会出错。

• 比如：在2 3这个数组中找到第一个大于等于3的元素。
• 比如：在2 3 3 3 3 4 4 4 4这个数组中找到第一个大于等于4的元素。

倒过来怎么做

那现在，如果你面临一个新的问题：

• 有一个从小到大排好序的数组，你要找到从右向左数第一个小于等于x的数字，应该怎么做？

问题：输入n，x，以及一个长度为n的数组a（已经从小到大排好序了）

输入样例：

9 4

2 3 3 3 3 4 4 4 4

应该这样修改程序？比如，这样：

int L = n-1, R = 0; // ???太迷惑了

很多小白可能会写出L = n-1, R = 0的初始条件（因为我们是从右向左数），然后比葫芦画瓢找到第一个小于等于x的数字。但是这样做太令人迷惑了，直觉上我们都觉得应该是L < R或者low < high，但是有些问题的“可行区间左端点”会比“可行区间右端点”要大，于是就会出现上面这段迷惑的代码。

显然，这样做会给我们思考带来很大的阻碍，这样是不符合直觉的，在写一些边界条件的式子的时候更可能出现错误。其实，我们往往可以通过问题转化，在写代码的时候把条件转化为L < R。比如在这个例子中，我们可以把问题转化为“找到从左往右数最后一个小于等于x的数字”，这时候就可以写出L = 0, R = n-1这样的初始条件。

通用做法

有些复杂的问题，进行问题转换也是较为困难的，因此我们需要总结出一个不费脑子、不需要思考就可以写出优美代码的做法。

我们注意到，二分查找的精髓在于，只通过a[M]的值来判断：答案是在左半边还是在右半边。

因此，我们只要抛弃传统意义上的“大小”概念，牢牢抓住这一点进行分析，仔细推断出这个条件用到的表达式，就一定可以写出优美的代码。

伪代码如下：

while( L < R ) {
    int M = L + (R - L)/2;
    if( 答案在[M + 1,R]中 ) { // 思考一下，什么情况下能够说明“答案在[M + 1,R]中”
        L = M + 1;
    } else { // 答案在[L,M]中
        R = M;
    }
}

有时候有死循环问题，LR的值更新后没有变化的时候

只需要把中点计算公式变成M = L + (R - L + 1)/2即可。在之前的中点计算公式M = L + (R - L)/2中，我们如果遇到了中点不是整数的情况，则会把中点向下取整，因此在出现L + 1 == R这种情况的时候就会始终有L == M从而引发问题。现在我们通过一个+1使得在中点不是整数的时候把中点向上取整，就可以避免这个问题（请在纸上模拟代码的运行过程，以体会这个公式是如何解决“差一点”问题的）。

// 在数组中找到从左往右大于等于x的数字的位置
if( 答案在[M + 1,R]中 ) {
    L = M + 1;
} else {
    R = M; // 这里可能引发“差一点”问题
}

建议你记住下述规律：

• 如果代码中是用的L = M，把L不断往右push，那么M向上取整（M = L + (R - L + 1)/2）；
• 如果代码中是用的R = M，把R不断往左push，那么M向下取整（M = L + (R - L)/2）。

总结

二分查找可能会遇到哪些边界情况？为什么示例代码能完美的解决这些边界情况？

答：总是可以通过问题转换写出满足L < R的优美代码。

• 二分查找伪代码

while( L < R ) {
    int M = L + (R - L)/2;
    if( 答案在[M + 1,R]中 ) { // 思考一下，什么情况下能够说明“答案在[M+1,R]中”
        L = M + 1;
    } else { // 答案在[L,M]中
        R = M;
    }
}

• 写二分查找遇到了死循环，考虑是不是遇到了“差一点”问题。

  • 如果代码中是用的L = M，把L不断往右push，那么M向上取整（M = L + (R - L + 1)/2）；
  • 如果代码中是用的R = M，把R不断往左push，那么M向下取整（M = L + (R - L)/2）。

• 代码示例：

  • 有一个从小到大排好序的数组，你要找到第一个大于等于x的数字，应该怎么做？

  输入n，x，以及一个长度为n的数组a（已经从小到大排好序了）

  输入样例：

  9 4

  2 3 3 3 3 4 4 4 4

  • 代码样例：

#include 
using namespace std;

int n, x, a[100000];

int main() {
    cin >> n >> x; // n为数组元素个数，x为
    // 输入数组
    for( int i = 0; i < n; ++i ) 
        cin >> a[i];
    // 考虑数组中不存在大于等于x的数字的情况
    if( x > a[n-1] ) {           
        cout << -1 << endl;
        return 0;
    }
    
    // 二分查找
    int L = 0, R = n-1;          // 数组下标从0到n-1，闭区间
    while( L < R ) {             // 当区间中至少有两个数字的时候，需要继续二分
        int M = L + (R - L) / 2; // 求出区间中点
        if( a[M] < x ) {         // 答案一定出现在[M+1,R]中
            L = M + 1;
        } else {                 // a[M] >= x，答案一定出现在[L,M]中
            R = M;
        }
    }
    // 此时L == R，a[L]就是第一个大于等于x的数字
    if ( a[L] == x) {
        cout << L << endl;  // 如果答案存在，则输出答案
    } else {
        cout << -1 << endl; // 如果答案不存在，则输出-1
    }
    return 0;
}

• 最后，再回顾一下在上一知识点中，我们推导了二分查找的时间复杂度。只有当我们询问区间中点的时候，我们才能让可行区间的长度以最快的速度变短——每次大约变为原来长度的一半，所以二分查找的时间复杂度是$lo{g}_2(n)$。

  二分查找时间复杂度的计算方法：

  比如，在猜数字的游戏中，假设我们一开始有n个数字。每次把剩余数字的区间分成两半，直x次后只剩下最后一个数字，就是我们想要的答案啦。 计算公式如下：

  $n\ast 1/(2^x)=1$

  x次后只剩下最后一个数字

  $x=lo{g}_2(n)$

  那么，x的值就是$lo{g}_2(n)$

二分查找算法的应用范围

有序才能二分查找

如果我们想要在一个数组上进行二分查找，那么这个数组必须是有序的，不管是升序还是降序，它必须是有序的。为什么呢？

注意二分查找的本质是什么：通过比较数组中间那个值和我们要求的值的关系，来判断出“答案不可能出现在数组的某一半”，从而让我们的查找范围缩小为原来的一半。

这也就是为什么我们要求数组中的元素是满足单调性的：只有这样，我们才能保证当a[M]不满足条件的时候，它左边（或者右边）的所有元素都不满足条件。

比如，我们要在一个升序的数组中找到第一个大于等于12的数字：

而我们在某次二分中发现a[M] = 7，由于数组是升序的，我们就可以判断出12一定出现在a[M]的右边。如果数组是乱序的，我们就无法得到任何有用的信息。

那么是不是任何有序的数据结构都可以应用二分查找算法呢？

其他有序结构

日期

日期是一个天然有序的结构：我们可以定义日期A小于日期B意为：在日历上A排在B的前面。比较两个日期的大小也可以通过很简单的方式进行：先比较年，再比较月，最后比较日。

struct Date {
    int year, month, day;
};
bool operator<( const Date &a, const Date &b ) {
    if( a.year == b.year ) {
        if( a.month == b.month ) {
            return a.day < b.day;
        } else {
            return a.month < b.month;
        }
    } else {
        return a.year < b.year;
    }
}

看起来只是一组三维数据而已，和二维数据的处理没什么差别？

但是我们可能会面临一个问题：如果我们要在公元1年1月1日和1000000000年1月1日之间二分，我们该如何求出两个日期的中点呢？

我们把日期表示成YYYYMMDD的形式，比如公元1年1月1日就是00010101，1000000000年1月1日就是10000000000101。则两个日期的中点，就是两个数字的中点，只不过我们需要把这个数字向下取整（或者向上取整）到最近的合法的日期。

比如，我们要求19701212和20200817的中点，我们可以直接求(19701212 + 20200827) / 2 = 19951019，这就是这两个日期的近似中点。如果我们得到了类似于19971805这样不合法的日期（没有18月），我们只需要把18月向下取整到合法的日期（12月），变为19971205即可。

字符串

字符串也是一个天然有序的数据结构：字典序就是字符串的大小顺序。因此我们可以给一堆字符串按照字典序排序。

string s[100];
for( int i = 0; i < n; ++i )
    cin >> s[i];
// sort函数用于给数组中的元素排序
sort(s, s+n); // string类的比较函数为比较两个字符串的字典序

现在在一堆排好序的字符串中，我们要找出所有前缀是com的字符串，应该怎么做呢？

apple
awsl
bag
bed
comm
commute
compare
cooperate

容易发现，所有前缀是com的字符串，在数组中也是一个连续的区间。

我们可以把数组中的所有字符串截断到前3位，然后使用二分查找法找到第一个com出现的位置和最后一个com出现的位置。

在这之间的所有字符串，前缀都是com。

二维数据

有的时候我们需要用到二维数据，比如平面中的点，就需要两个数字来表示，再比如std::pair这个数据结构，就是简单地把两个数字组合在一起。

不妨假设我们遇到的二维数据都是下面这样子的。类似平面上的整数点，一个点用两个整数(x,y)表示。

struct Point {
    int x, y;
};
// 这是运算符重载，当我们在代码中用小于号比较两个Point类变量的时候，就会用这个函数进行比较
bool operator<( const Point &a, const Point &b ) { // 如何定义a < b
    if( a.x == b.x ) {
        return a.y < b.y;
    } else {
        return a.x < b.x;
    }
}

这里我们定义了一种常用的比较二维数据的方法：首先比较两个数据的第一维，数字小的排在前面，当第一维数字相同的时候，比较第二维，数字小的排在前面。比如(3,3) < (4,2)，因为先比较第一维3 < 4。再比如(2,3) < (2,5)，因为第一维相同时比较第二维。

如果我们有一个排好序的Point数组，我们想找到数组中所有x = 5的元素（容易发现所有x = 5的元素在数组中一定是一个连续的区间），应该怎么做呢？

一个排好序的Point数组例子：(1,2), (2,3), (2,4), (5,-1), (5,2), (5,5), (7,4)。

Point a[100000];
for( int i = 0; i < n; ++i )
    cin >> a[i].x >> a[i].y;
sort(a, a+n); // sort函数可以给数组中的元素排序

我们只需要两次二分查找就可以了：分别找到第一个大于等于Point(5, INT_MIN)的元素，以及最后一个小于等于Point(5, INT_MAX)的元素。这两个元素中间的所有元素就是x = 5的所有元素（闭区间）。INT_MIN和INT_MAX分别是int所能表达的最小值和最大值。

总结

如果我们想要在一个数组上进行二分查找，那么这个数组必须是有序的，不管是升序还是降序，它必须是有序的。

为什么呢？

注意二分查找的本质是什么：通过比较数组中间那个值和我们要求的值的关系，来判断出“答案不可能出现在数组的某一半”，从而让我们的查找范围缩小为原来的一半。

这也就是为什么我们要求数组中的元素是满足单调性的：只有这样，我们才能保证当a[M]不满足条件的时候，它左边（或者右边）的所有元素都不满足条件。

所以：

• 要进行二分，数组必须是有序的。
• 基本上所有可以比较的数据都可以进行二分查找。
  • 比如：日期、字符串、二维数组
• 如果数据可以方便的计算“中点”，那么就可以在大区间上二分查找指定的数据（比如日期）