NLP学习-Task1:简介和词向量Word Vectors
更新流程↓
Task 1: 简介和词向量Word Vectors
Task 2: 词向量和词义Word Senses
Task 3: 子词模型Subword Models
Task 4: Contextual词嵌入
Task 5: 大作业
哈哈哈
当外地小伙转学到四川学校
阴阳怪气第一人
文章目录
-
- 1. 简介Introduction
-
- 1.1. 语言学到自然语言处理简要介绍
- 1.2. 人类语言和单词含义
- 2. 词表示模型
-
- 2.1. 离散表示one-hot representation
- 2.2. 分布表示distributional representation
- 2.3. 分布式表示distribution representation
-
- 2.3.1. 词嵌入word embedding
- 3. Word2vec语言模型的简要介绍
-
- 3.1.Word2vec目标函数梯度
- 3.2. 优化基础知识
-
- 3.2.1. 梯度下降
- 3.2.2. SGD随机梯度下降
- 4. 参考链接
1. 简介Introduction
1.1. 语言学到自然语言处理简要介绍
人类比猩猩更加聪明,是因为人们可以通过语言进行交互,对语言的理解和思考,展现了人类语言的复杂和高效。
每个人对于语言都可以有自己的理解,因此语言不光具有信息传递的功能,还可以通过语言来影响其他人。
当今社会,网络速度不断更新迭代,5G已经油然而生,相对于人类语言,我们使用NLP技术可以高速学习构建更强大的处理能力。
NLP就是对各种文本内容进行处理。
1.2. 人类语言和单词含义
Q1: How do we represent the meaning of a word?
定义含义:
- 用单词、词组表示概念
- 人们运用单词、符号表示自己的观点
- 通过写作作品、艺术来表达观
- 理解含义最普遍的语言方式 (denotational semantics用语言符号对语义进行转化):signifier(symbol)⇔signified(idea or thing)
Q2: How do we have usable meaning in a computer?
通常的解决方案:WordNet,Wordnet是一个包含同义词集和上位词(用 “is a”来表示关系的词集列表)的巨大词典。

Q3: Problems with resources like WordNet
WordNet的劣势:
- 是很好的resources,但忽略了细微的一些差别,例:proficient与good在词典中被认为是同义词,但事实上这只在某些文本上下文中成立。
- 忽略了一些单词的含义(即含义不完整)
- 偏主观(缺少客观性)
- 需要人类来不断地更新和改写
- 无法计算单词之间的相似度
2. 词表示模型
词向量Word Vectors,将单词编码成向量,将其表示成在词空间中的某一点。每一维都可看作是某些语义信息的编码。
在NLP中有三种方法将词表示在计算机中:离散表示one-hot representation、分布表示distributional representation和分布式表示distribution representation。
- Distribution:分布式描述的是若干元素的连续表示形式,如稠密的词嵌入向量表示、Word2vec,与之相反的是独热向量。
- Distributional:使用词语的上下文来表示其语义,基于计数的词向量表示就是分布表示,因为我们都使用词语的上下文来表征它的含义。
2.1. 离散表示one-hot representation
传统的基于规则或基于统计的自然语义处理方法将单词看作一个原子符号,被称作离散表示one-hot representation。
离散表示把每个词表示为一个长向量。这个向量的维度是词表大小,向量中只有一个维度的值为1,其余维度为0,这个维度就代表了当前的词。
# e.g.
motel = [0 0 0 0 0 0 0 0 0 0 1 0 0 0 0]
hotel = [0 0 0 0 0 0 0 1 0 0 0 0 0 0 0]
离散表示相当于给每个词分配一个id,这就导致这种表示方式不能展示词与词之间的关系。另外,离散表示将会导致特征空间非常大,但也带来一个好处,就是在高维空间中,很多应用任务线性可分。
2.2. 分布表示distributional representation
分布表示distributional representation:是基于分布假设理论,利用共生矩阵来获取词的语义表示,可以看成是一类获取词表示的方法。
什么是分布假说呢?词是承载语义的最基本的单元,而传统的独热表示仅仅将词符号化,不包含任何语义信息。如何将语义融入到词表示中?Harris 在 1954 年提出的分布假说(distributional hypothesis)为这一设想提供了理论基础:上下文相似的词,其语义也相似。
“这里的分布”与中文“统计分布”一词语义对应,描述的是上下文的概率分布。用上下文描述语义的表示方法(或基于分布假说的方法)都可以称作分布表示,如潜在语义分析模型(Latent Semantic Analysis, LSA)、潜在狄利克雷分配模型(Latent Dirichlet Allocation,LDA)等。
2.3. 分布式表示distribution representation
分布式表示distribution representation包括基于矩阵、基于聚类、基于神经网络的方式,一般将基于神经网络的分布式表示称为词嵌入word embedding。而词嵌入又包括很多不同的算法集合,或者叫做实现工具,比如SEENA、FastText、word2vec等。
分布式表示优点:
- 词之间存在相似关系: 是词之间存在“距离”概念,这对很多自然语言处理的任务非常有帮助。
- 包含更多信息: 词向量能够包含更多信息,并且每一维都有特定的含义。在采用one-hot特征时,可以对特征向量进行删减,词向量则不能。
2.3.1. 词嵌入word embedding
词嵌入word embedding,又叫Word嵌入式自然语言处理(NLP)中的一组语言建模和特征学习技术的统称,其中来自词汇表的单词或短语被映射到实数的向量。 从概念上讲,它涉及从每个单词一维的空间到具有更低维度的连续向量空间的数学嵌入。
生成这种映射的方法包括神经网络,单词共生矩阵的降维,概率模型,可解释的知识库方法,和术语的显式表示单词出现的背景。
当用作底层输入表示时,单词和短语嵌入已经被证明可以提高NLP任务的性能,例如语法分析和情感分析。
词嵌入技术是将词转化成为稠密向量,并且对于相似的词,其对应的词嵌入也相近。

3. Word2vec语言模型的简要介绍
如果用一句比较简单的话来总结,word2vec是用一个一层的神经网络(即CBOW)把one-hot形式的稀疏词向量映射称为一个n维(n一般为几百)的稠密向量的过程。为了加快模型训练速度,其中的tricks包括Hierarchical softmax,negative sampling, Huffman Tree等。
在NLP中,最细粒度的对象是词语。如果我们要进行词性标注,用一般的思路,我们可以有一系列的样本数据(x,y)。其中x表示词语,y表示词性。而我们要做的,就是找到一个x -> y的映射关系,传统的方法包括Bayes,SVM等算法。但是我们的数学模型,一般都是数值型的输入。但是NLP中的词语,是人类的抽象总结,是符号形式的(比如中文、英文、拉丁文等等),所以需要把他们转换成数值形式,或者说通过词嵌入的方式将它嵌入到一个数学空间里,而Word2vec就是词嵌入的一种。
在NLP中,把x看做一个句子里的一个词语,y 是这个词语的上下文词语,那么这里的f,便是NLP中经常出现的语言模型(language model),这个模型的目的,就是判断 (x,y) 这个样本,是否符合自然语言的法则,更通俗点说就是:词语x和词语y放在一起。
Word2vec正是来源于这个思想,但它的最终目的,不是要把 f 训练得多么完美,而是只关心模型训练完后的副产物——模型参数(这里特指神经网络的权重),并将这些参数,作为输入 x 的某种向量化的表示,这个向量便叫做——词向量。
Word2vec的特点
- 包含大量的文本语料
- 固定词表中的每一个单词由一个词向量表示
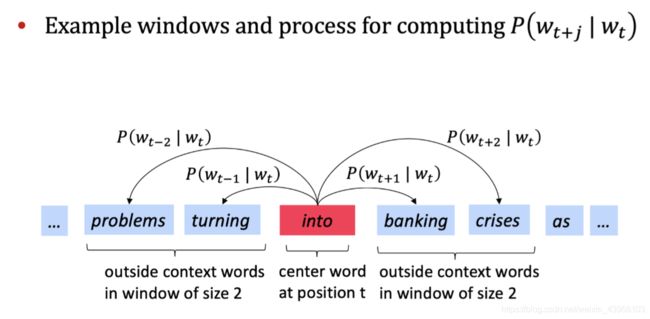
- 遍历本文中的每个位置 t t t,包含了center word中心词 c c c,和context words上下文 o o o(除了 c c c的外部单词)。
- 通过 c c c和 o o o的词向量相似性来计算 P ( o / c ) P(o/c) P(o/c)
- 调整优化word vectors来最小化似然,最大化概率
Word2vec的目标函数:
对于每一个文本的位置 t = 1 , 2 , . . . , T t = 1,2,...,T t=1,2,...,T,预测窗口为 m m m的上下文,给出中心词 w j w_{j} wj:
l i k e l i h o o d = L ( θ ) = ∏ t = 1 T ∏ − m ≤ j ≤ m j ≠ 0 p ( w t + j ∣ w t ; θ ) likelihood=L(\theta)=\prod_{t=1}^{T}\prod_{-m \le j \le m\ \ \ \ \ j\ne0}^{}p(w_{t+j}|w_t;\theta) likelihood=L(θ)=t=1∏T−m≤j≤m j=0∏p(wt+j∣wt;θ)
注: θ \theta θ 是需要优化的参数
J ( θ ) = − 1 T l o g L ( θ ) = − 1 T ∑ t = 1 T ∑ − m ≤ j ≤ m j ≠ 0 l o g P ( w t + j ∣ w t ; θ ) J(\theta)=-\frac 1TlogL(\theta)=-\frac1T\sum_{t=1}^T\sum_{-m\le j\le m \ \ \ \ \ j\ne 0}logP(w_{t+j}|w_t;\theta) J(θ)=−T1logL(θ)=−T1t=1∑T−m≤j≤m j=0∑logP(wt+j∣wt;θ)
- 损失函数 J ( θ ) J(\theta) J(θ)是(平均)负的对数似然(negative log likelihood);
- 负号将极大化损失函数转化为极小化损失函数;
- log函数方便将乘法转化为求和(优化处理)
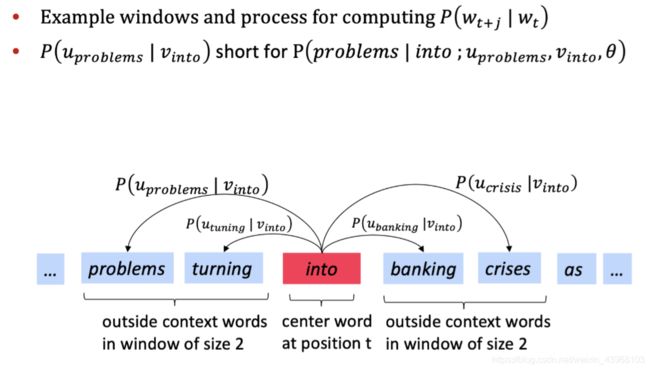
Q:如何计算 P ( w t + j ∣ w t ; θ ) P(w_{t+j}|w_t;\theta) P(wt+j∣wt;θ)?
A:对于每个单词 w 我们使用两个向量 v w v_w vw(当 w w w是中心词时)和 u w u_w uw(当 w w w是上下文单词时),对于中心词 c c c和上下文单词 o o o,有: P ( o ∣ c ) = e x p ( u o T v c ) ∑ w ϵ V e x p ( u w T v c ) P(o|c)=\frac {exp(u_o^Tv_c)}{\sum_{w\epsilon V}exp(u_w^Tv_c)} P(o∣c)=∑wϵVexp(uwTvc)exp(uoTvc)
在概率函数中: P ( o ∣ c ) = e x p ( u o T v c ) ∑ w ϵ V e x p ( u w T v c ) P(o|c)=\frac {exp(u_o^Tv_c)}{\sum_{w\epsilon V}exp(u_w^Tv_c)} P(o∣c)=∑wϵVexp(uwTvc)exp(uoTvc)
- 分子取幂函数使得始终可以为正
- 向量 u o u_o uo 和向量 v c v_c vc 点乘,点乘结果越大,向量之间越相似
- u T v = u ⋅ v = ∑ i = 1 n u i v i u^Tv=u·v=\sum_{i=1}^nu_iv_i uTv=u⋅v=∑i=1nuivi
- 对整个词表标准化,给出概率分布
softmax函数进行归一化(深度学习中常用): R n → R n \Bbb{R^n}\to \Bbb{R^n} Rn→Rn s o f t m a x ( x ) = e x p ( x i ) ∑ j = 1 n e x p ( x j ) = p i softmax(x)= \frac {exp(x_i)}{\sum_{j=1}^nexp(x_j)}=p_i softmax(x)=∑j=1nexp(xj)exp(xi)=pi 注:用于将任意值 x i x_i xi 映射到概率分布 p i p_i pi。
3.1.Word2vec目标函数梯度
训练模型:计算所有矢量渐变
整个模型里只有一个参数 θ \theta θ ,所以我们只用优化这一个参数就行。
例如:模型在一个 d d d维,词典大小为 V V V:
θ = [ v a a r d v a r k v a . . . v z e b r a u a a r d v a r k u a . . . u z e b r a ] ∈ R 2 d V \theta =\begin{bmatrix}v_{aardvark}\\ v_{a}\\...\\ v_{zebra}\\ u_{aardvark}\\ u_{a} \\ ...\\ u_{zebra}\end{bmatrix}\in \Bbb R^{2dV} θ=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡vaardvarkva...vzebrauaardvarkua...uzebra⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤∈R2dV
- 2:每个单词有两个向量
- 通过梯度(导数)下降的方式优化参数
- 梯度下降会用到链式法则
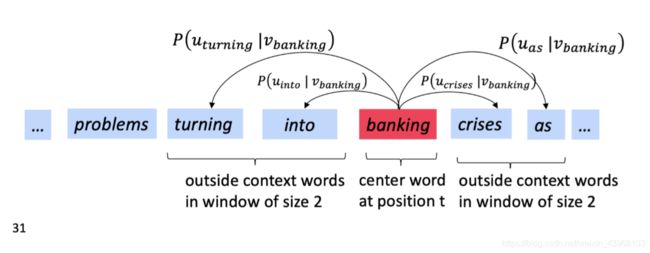
- 迭代计算每个中心词向量和上下文词向量随着滑动窗口移动的梯度
- 依次迭代更新窗口中所有的参数
3.2. 优化基础知识
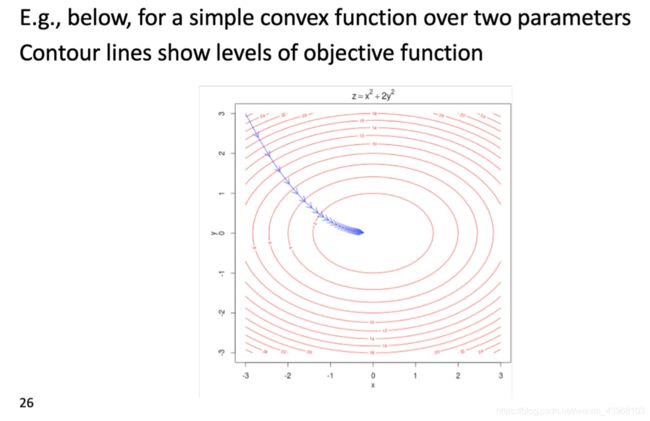
3.2.1. 梯度下降
- 我们的损失函数 J ( θ ) J(\theta) J(θ) 需要最小化
- 使用的方法为:梯度下降
- 对于当前 θ \theta θ ,计算 J ( θ ) J(\theta) J(θ) 的梯度
- 然后小步重复朝着负梯度方向更新方程里的参数 α = ( s t e p s i z e ) o r ( l e a r n i n g r a t e ) \alpha=(step\ size)\ or\ (learning\ rate) α=(step size) or (learning rate), θ n e w = θ o l d − α ∇ θ J ( θ ) \theta^{new}=\theta^{old}-\alpha \nabla_\theta J(\theta) θnew=θold−α∇θJ(θ)
- 更新唯一的参数 θ \theta θ: θ j n e w = θ j o l d − α α α θ j o l d J ( θ ) \theta_j^{new}=\theta_j^{old}-\alpha \frac \alpha{\alpha\ \theta_j^{old}}J(\theta) θjnew=θjold−αα θjoldαJ(θ)
while True:
theta_grad = evaluate_gradient(J,corpus,theta)
theta = theta - alpha * theta_grad
3.2.2. SGD随机梯度下降
- 由于 J ( θ ) J(\theta) J(θ)是在语料文本中所有窗口的方程
- 当语料很大的时候,计算梯度会消耗巨大
- 解决办法:SGD随机梯度下降
- 不断sample窗口,不断更新
while True:
window = sample_window(corpus)
theta_grad = evaluate_gradient(J,window,theta)
theta = tehta - alpha * theta_grad
4. 参考链接
- 【2019 CS224N 中文字幕】Stanford CS224N NLP with Deep Learning Winter
- datawhalechina / team-learning / 04 自然语言处理 / Lecture / Lecture1 / reference
- 百度百科——词向量
- 什么是词向量?(NPL入门)
- 小白都能理解的通俗易懂word2vec详解
- Lecture1- Introduction and Word Vectors 斯坦福 nlp 教程
- 词向量Word Vectors学习笔记–word2vec
- 分布表示(distributional representation)与分布式表示(distributed representation)
- word2vec和word embedding有什么区别?
- [NLP] 秒懂词向量Word2vec的本质