Huffman编码
目录
- 背景
- Huffman编码
- 代码部分
背景
英文字母大小写总共就52个,一本英文书籍几十上百万的英文单词都是由这52个字符排列组合而成,不难看出这52个字符肯定是大量重复了。
一本中文小说几百万字,也都是由常用的几千个汉字组合而成。如果是一本玄幻小说,那么在相近的章节中一定大量的重复出现人名,地名,功法境界,以及主角在一段时间内修炼的功法。至于主角名字更是贯穿整本小说一定大量重复。还有作者的写作风格是保持一致的,因此文章有时候在描写一些紧张氛围或者描写反面人物可能会使用相似的句式和词语来表达,这些可能会造成很高的重复率。
图片是由像素点组成的而每个像素点是由rgb:三元素组成。这些都是由0~255的数字表示,因此可以将图片看作一堆数字。一张小的图片的像素点至少也有几千,如果是高清图片估计有上百万个像素点。每一个像素点都是三个0~255的数字,组成图片的像素点一定存在大量的重复数字;一些图片有很大范围的背景色这种情况下,数字更是会发生大量的重复。
不管是中文,英文还是图片的像素点,如果数据量很大那么肯定存在大量重复字符。一个英文字符是8bit,一个中文字符使用UTF-8编码会占3个字节24bit;如果要压缩数据,从字符编码角度考虑应该怎么去压缩呢?可以思考三秒(PS:就这几段句子已经重复出现重复了很多次了)
Huffman编码
现在有一段英文文本AAAAAAAAABBCCCDDCCCBBBAAAAABB,这段文本A 出现14次,B出现7次,C出现6次,D出现2次。正常编码,这个文本所占bit:(14+7+6+2)* 8 = 232bit。
A的编码是:0100 0001B的编码是:0100 0010C的编码是:0100 0011D的编码是:0100 0100
我们可以思考下,A,B,C,D这四个字符在这段文本中需要用8bit来表示吗?是不是可以用更少的字符来表示这几个字符?重新给这4个字符编码:
A->1B->10C->11D->100
重新编码之后,这段文本所占bit:14 * 1 + 2 * 7 + 2 * 6 + 2 * 3 = 46bit;重新编码之后的文本大小只占原文本的20%左右。在这个例子中,A编码最短,BC次之,D最长我们是按照字母顺序来编码的吗?显然不是的,在给字符编码时,是按照字符使用的频率来决定该如何编码。如果使用次数多也就是频率高的就尽量用短编码,使用次数少频率低就用长编码。这样才能尽可能的降低压缩后的字符长度。Huffman编码在对字符重新编码时的指导思想就是这样的。
我们继续上面的例子,将A,B,C,D按照上面的方法编码并创建一个对照表。
| A | B | C | D |
|---|---|---|---|
| 1 | 10 | 11 | 100 |
根据重新编码后的字符,上面英文文本的二进制编码是 :111111111101011111110010011110111111101010111111010,根据这段编码我们该如何解码,将压缩后的二进制码还原成字符?
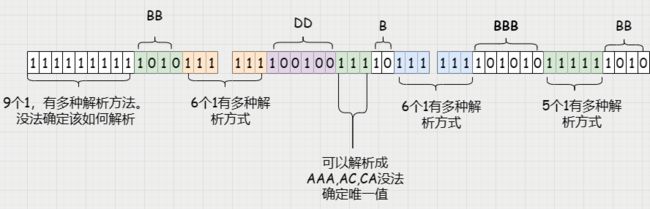
根据上面的编码我们可以看出,在解压时没法恢复源文本了。最开始的9个1,可以有多种解析方式:可以4个C 一个A,这种情况下A位置变化都有5种。还可以有3C,3A的组合。。。。等等其他组合根本没有办法确定这9个1该如何编码。
那该如何编码呢?既要按照字符使用频率来编码,又要在解压时能够复原文本。这时候Huffman树就隆重出场了Huffman树的构建很简单,但是构建过程非常巧妙。Huffman树的构建规则:
- Huffman树是一个二叉树
- 所有字符节点都是叶子节点
- 每次都用2个最少使用频率节点来构建新节点;
这是我自己总结的构造Huffman树的规则,看不懂太正常,在我第一次接触Huffman树估计也是看不懂。下面会用上面的例子图解如何构建一颗Huffman树。

最开始有 A,B,C,D四个节点,经过排序之后由较小的2个节点生成新的节点。因此选择C,D来生成新节点:8;生成新节点之后C,D节点不再参与后续的过程。
参与第二次构建Huffman树的新节点:8,B(7),A(14),这3个节点再比较使用次数: 7 < 8 < 14 ;因此使用 B(7),8节点来构建新节点:15;
第三次参与构建新节点的的节点: 15,A(14);直接用这2个节点生成root节点;Huffman树构建结束。
可以看出来,使用频率最高的A,从根节点到A的路径是最短的,而使用频率最小的D,从根节点到D的距离是最长的。这路劲长短正好对应了使用频率的高低。如果一个节点链接left节点用 0 表示;链接 right 节点用 1表示;(反过来也可以)那么从root节点到叶子节点的路径就可以用01字符串来表示了;

A,B,C,D构建的Huffman树形成了新的编码:
| A | B | C | D |
|---|---|---|---|
| 1 | 01 | 001 | 000 |
英文:AAAAAAAAABBCCCDDCCCBBBAAAAABB经过构建Huffman树重新编码之后的压缩文本是:1111111110101001001001000000001001001010101111110101一共52字符;只有原文的52/232 = 22%左右大小;
回到关键问题,如何解压呢?
也很简单,在解压时只需要对照Huffman树来解压就行。从root节点往下找,找到叶子节点就找到了对应的字符。用这种方式顺序读取二进制码对照Huffman树就可以解析文本了。

代码部分
- Huffman树的构建:
//Huffman树节点
class HMNode{
int val;
HMNode left;
HMNode right;
boolean leaf;//是否叶子节点
char str;
public HMNode(int val){
this.val = val;
}
public HMNode(int val,char str){
this.val = val;
leaf = true;
this.str = str;
}
@Override
public String toString() {
return "val="+val+";char="+(str=='\0' ? '_':str);
}
}
//统计文本各个字符使用频率
public Map<Character,Integer> count(String text){
Map<Character,Integer> map = new HashMap<>();
for (int i = 0; i <text.length() ; i++) {
char t = text.charAt(i);
if(map.containsKey(t)){
map.compute(t,(key,val)->val+1);
}else{
map.computeIfAbsent(t,key->1);
}
}
return map;
}
//构建Huffman树
public HMNode buildHuffManTree(String text){
Map<Character,Integer> map = count(text);
List<HMNode> nodes = new ArrayList<>(map.size()<<1);
map.forEach((key,val)->nodes.add(new HMNode(val,key)));
nodes.sort((n1, n2)-> n1.val-n2.val);
int start = 0;
while(nodes.size()-2>=start){
HMNode root = new HMNode(nodes.get(start).val+nodes.get(start+1).val);
root.left = nodes.get(start);
root.right = nodes.get(start+1);
nodes.add(root);
nodes.sort((n1, n2)-> n1.val-n2.val);
start+=2;
}
return nodes.get(start);
}
- 测试
@Test
public void test(){
String text = "aaabbbbbccccccddddee";
HMNode root =buildHuffManTree(text);
List nodes = new ArrayList();
nodes.add(root);
print(nodes);
}
public void print(List<HMNode>nodes){
List<HMNode> c = new ArrayList<>();
System.out.println("\n");
for (HMNode hmNode : nodes){
if(hmNode.left != null)c.add(hmNode.left);
if(hmNode.right != null)c.add(hmNode.right);
System.out.print(hmNode+ "\t");
}
System.out.println("\n");
if(!c.isEmpty())print(c);
}
=========================================res=================================================
//结果:char=_ ===> 表示新生成的节点
val=20;char=_
val=9;char=_ val=11;char=_
val=4;char=d val=5;char=b val=5;char=_ val=6;char=c
val=2;char=e val=3;char=a
- 将Huffman树转化成编码
//左分支 + 0 ; 右分支 + 1
public void huffmanCode(HMNode root,Map<String,Character> huffmanCode,String code){
if(root.leaf){
huffmanCode.put(code,root.str);
return;
}
if(root.left != null){
huffmanCode(root.left,huffmanCode,code+"0");
}
if(root.right != null){
huffmanCode(root.right,huffmanCode,code+"1");
}
}
@Test
public void test(){
String text = "aaabbbbbccccccddddee";
Map<Character, Integer> count = count(text);
HMNode root =buildHuffManTree(text);
Map<String,Character>code = new HashMap<>();
huffmanCode(root,code,"");
code.forEach((key,val)->System.out.println(val+" -> "+key));
}
=========================================res=================================================
d -> 00
c -> 11
b -> 01
e -> 100
a -> 101
后续:Huffman 二进制码以及文本压缩与解压