初始化及分布
目录
- 参考地址
- 1. 计算增益 calculate_gain()
- 2. 均匀分布 X X X ~ U ( a , b ) U(a,b) U(a,b)
- 3. 正态分布 X X X ~ N ( m e a n , s t d 2 ) N(mean,std^2) N(mean,std2)
- 4. 截断正态分布 trunc_normal_
- 5. 初始化为常量constant、ones、zeros、eye、dirac
- 6. Glorot initialization:xavier_uniform_()和xavier_normal_()
- 7. He initialization:kaiming_uniform_()和kaiming_normal_()
参考地址
很棒的博客:pytorch系列 – 9 pytorch nn.init 中实现的初始化函数 uniform, normal, const, Xavier, He initialization
官网初始化文档:torch.nn.init
这些函数的最后面都带了一个下划线_,表示就地操作。(即,直接改变原值,不会传回新的副本)
1. 计算增益 calculate_gain()
torch.nn.init.calculate_gain(nonlinearity, param=None)
返回给定非线性函数(nonlinearity)的建议增益值(gain)。数值如下:
param参数默认为空(None),只有Leaky Relu才会用到这个param参数,且默认大小为0.01。即:
- negative_slope = 0.01( if param is None )
- negative_slope = param
| nonlinearity | gain |
|---|---|
| Linear / Identity | 1 |
| Conv{1,2,3}D | 1 |
| Sigmoid | 1 |
| Tanh | 5 3 \frac{5}{3} 35 |
| ReLU | 2 \sqrt{2} 2 |
| Leaky Relu | 2 1 + negative_slope 2 \sqrt{\frac{2}{1 + \text{negative\_slope}^2}} 1+negative_slope22 |
| SELU | 3 4 \frac{3}{4} 43 |
2. 均匀分布 X X X ~ U ( a , b ) U(a,b) U(a,b)
默认为0-1均匀分布,即(x,y) ~ U(0,1)
torch.nn.init.uniform_(tensor, a=0.0, b=1.0)
均匀分布概念:均匀分布
均匀分布:Uniform Distribution
3. 正态分布 X X X ~ N ( m e a n , s t d 2 ) N(mean,std^2) N(mean,std2)
默认为0-1标准正态分布,即(x,y) ~ N(0,1)
注意:是依据均值 mean和方差 std^2的分布。(std是指标准差)
所以参考的【很棒的博客:pytorch系列 – 9 pytorch nn.init 中实现的初始化函数 uniform, normal, const, Xavier, He initialization】中对正态分布的写法有误。(写成了
服从 ~N(mean,std))
torch.nn.init.normal_(tensor, mean=0.0, std=1.0)
概念:正态分布-搜狗词条
正态分布:Normal Distribution
正态分布,也称高斯分布(Gaussian distribution)。
有关正态分布标准化的实际意义:正态分布标准化可以方便计算
参考链接:一文搞懂“正态分布”所有需要的知识点
关于正态分布均数和标准差的性质,我们这里简单总结一下:
1)概率密度曲线在均值处达到最大,并且对称;
2)一旦均值和标准差确定,正态分布曲线也就确定;
3)当X的取值向横轴左右两个方向无限延伸时,曲线的两个尾端也无限渐近横轴,理论上永远不会与之相交;
4)正态随机变量在特定区间上的取值概率由正态曲线下的面积给出,而且其曲线下的总面积等于1 ;
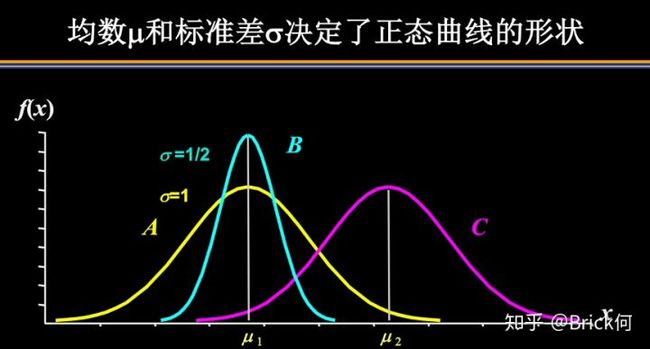
5)均值决定正态曲线的具体位置,可取实数轴上的任意数值;标准差决定曲线的矮胖、高瘦程度,即“陡峭”或“扁平”程度:标准差越大,正态曲线越扁平;标准差越小,正态曲线越陡峭。(即mean确定位置,std越大越矮胖,越小越高瘦)
这是因为,标准差越小,意味着大多数变量值离均数的距离越短,因此大多数值都紧密地聚集在均数周围,图形所能覆盖的变量值就少些(比如1±0.1涵盖[0.9,1.1]),于是都挤在一块,图形上呈现瘦高型。相反,标准差越大,数据跨度就比较大,分散程度大,所覆盖的变量值就越多(比如1±0.5涵盖[0.5,1.5]),图形呈现“矮胖型”。我们可以对照下图直观地看一下,图中黄色曲线为A,蓝色曲线为B,紫红色曲线为C。
标准化,z变换:
将正态分布标准化,也称z变换。通过标准化,所有服从一般正态分布的随机变量都变成了服从均数为0,标准差为1的标准正态分布。
完成z变换,我们就通过查看z值表找到对应的概率值。
再三强调,图中阴影部分的面积代表的是Z ≤ z的概率(重要的话讲三遍,注意是“≤”)。另外,还有两个根据定义成立的两个公式:
- P ( Z ≥ z ) = 1 − P ( Z ≤ z ) P(Z≥z)=1-P(Z≤z) P(Z≥z)=1−P(Z≤z)
- P ( Z ≤ − z ) = 1 − P ( Z ≤ z ) P(Z≤-z)=1-P(Z≤z) P(Z≤−z)=1−P(Z≤z)
三个百分数:68%,95%,99.7%
正态分布运用十分广泛的三个百分数:68%,95%,99.7%。
- 68%的概率在离平均值
1个标准差以内 - 95%的概率在离平均值
2个标准差以内 - 99.7%的概率在离平均值
3个标准差以内
例:某小学学生身高的平均值和标准差分别为1.4(米)和0.15(米),则可以推测:
- 这个学校有68%的学生的身高在1.25到1.55,这里的1.25和1.55就是1.4加减0.15得到的(均数加减一个标准差)
- 有95%的学生身高在1.1到1.7之间(均数加减两个标准差)
由此便极大地提升了我们对数据的掌握程度,反之也可以巧妙地求解均数和标准差。
4. 截断正态分布 trunc_normal_
默认为截断[-2,2]的[0-1标准正态分布。
这个部分在【官网初始化文档:torch.nn.init】中没有,但是在PyTorch的init.py文件中存在。
精简的解释:在截断范围之外,函数值为0。
截断正态分布:请教截尾正态分布是什么,相比于一般的正态分布,性质上有何区别? - 何云超的回答 - 知乎(原创!CSDN上的是抄的!)
- Normal Distribution称为正态分布,也称为高斯分布,Truncated Normal Distribution一般翻译为截断正态分布,也有称为截尾正态分布。
def trunc_normal_(tensor: Tensor, mean: float = 0., std: float = 1., a: float = -2., b: float = 2.) -> Tensor:
r"""Fills the input Tensor with values drawn from a truncated
normal distribution. The values are effectively drawn from the
normal distribution :math:`\mathcal{N}(\text{mean}, \text{std}^2)`
with values outside :math:`[a, b]` redrawn until they are within
the bounds. The method used for generating the random values works
best when :math:`a \leq \text{mean} \leq b`.
Args:
tensor: an n-dimensional `torch.Tensor`
mean: the mean of the normal distribution
std: the standard deviation of the normal distribution
a: the minimum cutoff value
b: the maximum cutoff value
Examples:
>>> w = torch.empty(3, 5)
>>> nn.init.trunc_normal_(w)
"""
return _no_grad_trunc_normal_(tensor, mean, std, a, b)
翻译:
用从截断正态分布中提取的值填充输入张量。这些值实际上来自正态分布: N ( mean , std 2 ) \mathcal{N}(\text{mean}, \text{std}^2) N(mean,std2),值在边界 [ a , b ] [a,b] [a,b]之外重画,直到它们在边界之内。用于生成随机值的方法在以下情况下效果最佳: a ≤ mean ≤ b a \leq \text{mean} \leq b a≤mean≤b
参数:
- tensor:输入的N维张量
- mean:正态分布的均值
default=0 - std:正态分布的标准差
default=1 - a:截断范围最小值
default=-2 - b:阶段范围最大值
default=2
5. 初始化为常量constant、ones、zeros、eye、dirac
初始化整个tensor为常量val。
torch.nn.init.constant_(tensor, val)
初始化整个tensor为1。
torch.nn.init.ones_(tensor)
初始化整个tensor为0。
torch.nn.init.zeros_(tensor)
tensor为二维,初始化为单位矩阵,当tensor的size不是正方形时,就沿着对角线填充最小边数个1。
torch.nn.init.eye_(tensor)
太菜了,看不懂/(ㄒoㄒ)/~~
torch.nn.init.dirac_(tensor, groups=1)
6. Glorot initialization:xavier_uniform_()和xavier_normal_()
“Xavier”初始化方法是一种很有效的神经网络初始化方法,方法来源于2010年的一篇论文:《Understanding the difficulty of training deep feedforward neural networks》
基本思想是通过网络层时,输入和输出的方差相同,包括前向传播和后向传播。
为了使得网络中信息更好的流动,每一层输出的方差应该尽量相等。
对于Xavier初始化方式,pytorch提供了uniform和normal两种:
torch.nn.init.xavier_uniform_(tensor, gain=1.0)均匀分布 ~ U ( − a , a ) U(-a,a) U(−a,a)
其中,a的计算公式:
a = gain × 6 fan_in+fan_out a=\operatorname{gain} \times \sqrt{\frac{6}{\text { fan\_in+fan\_out }}} a=gain× fan_in+fan_out 6
torch.nn.init.xavier_normal_(tensor, gain=1.0)正态分布 ~ N ( 0 , s t d 2 ) N(0,std^2) N(0,std2)
其中,std的计算公式:
s t d = g a i n × 2 fan_in + fan_out s t d=g a i n \times \sqrt{\frac{2}{\text { fan\_in }+\text { fan\_out }}} std=gain× fan_in + fan_out 2
其中, f a n _ i n fan\_in fan_in和 f a n _ o u t fan\_out fan_out的意思是:
- f a n _ i n fan\_in fan_in:前向传播中权重方差的大小
- f a n _ o u t fan\_out fan_out:反向传播中权重方差的大小
7. He initialization:kaiming_uniform_()和kaiming_normal_()
Xavier在tanh中表现的很好,但在Relu激活函数中表现的很差。
所以何凯明提出了针对于Relu的初始化方法。Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification He, K. et al. (2015)
该方法基于He initialization,其简单的思想是:
在ReLU网络中,假定每一层有一半的神经元被激活,另一半为0,所以,要保持方差不变,只需要在 Xavier 的基础上再除以2。也就是说在方差推导过程中,式子左侧除以2。
pytorch也提供了两个版本:
-
torch.nn.init.kaiming_uniform_(tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')均匀分布~ U ( − b o u n d , b o u n d ) U(-bound,bound) U(−bound,bound)
其中,bound的计算公式为:
bound = gain × 3 fan_mode \text { bound }=\text { gain } \times \sqrt{\frac{3}{\text { fan\_mode }}} bound = gain × fan_mode 3 -
torch.nn.init.kaiming_normal_(tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')正态分布~ N ( 0 , s t d 2 ) N(0,std^2) N(0,std2)
其中,std的计算公式为:
std = gain fan_mode \text { std }=\frac{\text { gain }}{\sqrt{\text { fan\_mode }}} std = fan_mode gain
其中:
- a:表示该层后面一层的激活函数中负的斜率(only used with ‘leaky_relu’)
- gain:表示增益,通过选择某种
非线性函数 nonlinearity(即’relu’等,默认为’leaky_relu’)操作在a上得到。 - f a n _ m o d e fan\_mode fan_mode:要么是 f a n _ i n fan\_in fan_in(默认模式)要么是 f a n _ i n fan\_in fan_in。分别表示前向传播、反向传播中权重方差的大小。
针对于Relu的激活函数,基本使用He initialization,pytorch也是使用kaiming 初始化卷积层参数的。
