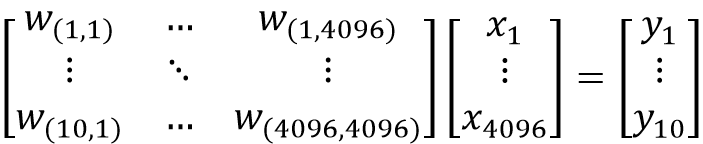Pytorch深度学习实践（b站刘二大人）P10讲 (CNN卷积神经网络基础篇)

1.全连接网络

指的是网络里面用的都是线性层，如果一个网络全都由线性层串行连接起来，就叫做全连接网络

在线性层里面输入和每一个输出值之间都存在权重，即每一个输入节点都要参与到下一层输出节点的计算上，这样的线性层也叫全连接层 Fully Connected

说到全连接层，大家马上就能反应到，CNN的最后一层大多是全连接层，全连接层可以实现最终的分类。那么为什么要叫全连接层呢？全连接层有什么特点呢？

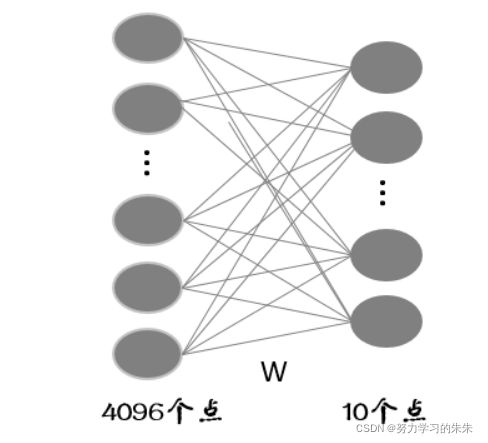
假设全连接层的输入是个4096维的列向量，一般我们把这个向量叫做特征向量（卷积层提取到的特征的输出），经过全连接层得到一个10维的列向量输出（也就是10分类每一类别的评分）。我们如果把输入和输出都看成一个个节点的话，节点与节点之间的关系可以用下图来表示：

可以看出，10个节点中每一个节点的输出都是通过4096个节点的输入得到的，也就是说，每一个输出节点受所有的输入节点影响，这样就会有 4096*10 个连接，每个连接上都会对应一个权重，则全连接层要训练 4096*10 个权重。之所以称之为全连接层，就是由于每一个输出节点与每一个输入节点都有连接。写成矩阵的形式为： 

 看这个矩阵的话，可以认为每一行的权重对应着一个类别的分类器，由于是10分类问题，所以有10行，即对应10个分类器。

2.二维卷积神经网络工作方式

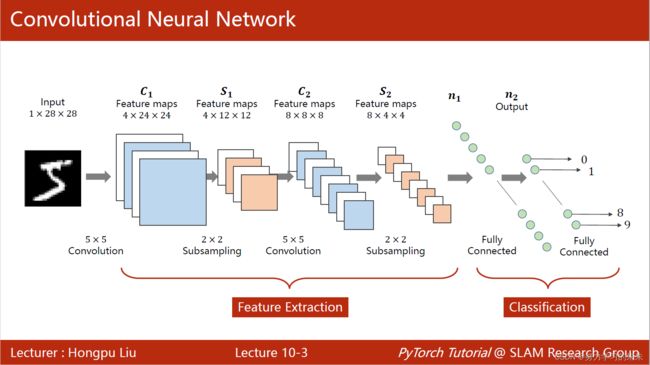 卷积神经网络把图像按照原始的空间结构保存，能保留原始的空间信息（全连接过程中，把图像弄成了一串，会使原本图像中相邻的节点，距离较远）
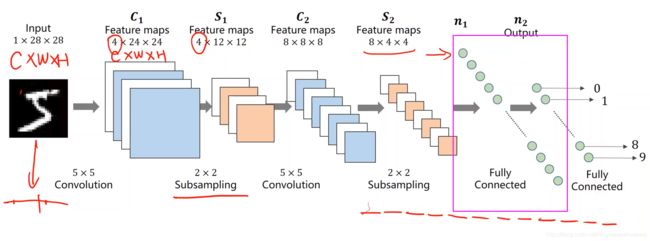
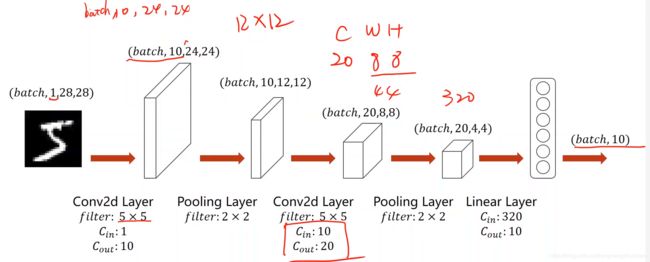
经过一个卷积层把1*28*28的图像变成4*24*24

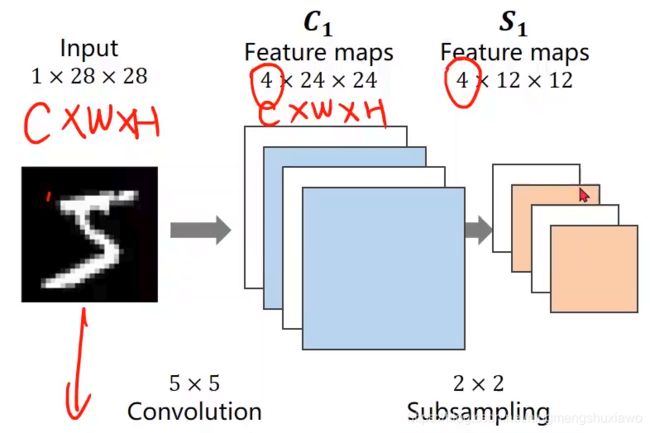
使用下采样（subsampling）时，通道数不会改变，图像的宽度和高度会改变，下采样的目的是减少数据的数据量，减少特征图（Feature map）的元素数量，目的是降低运算需求，因为是做分类，最终的目的是通过不断的卷积运算输出一个概率向量
现在输入的维度比较高，需要不断地进行维度（可以先升高后降低）和大小上的变化，最终把图像由1*28*28的张量变成概率向量

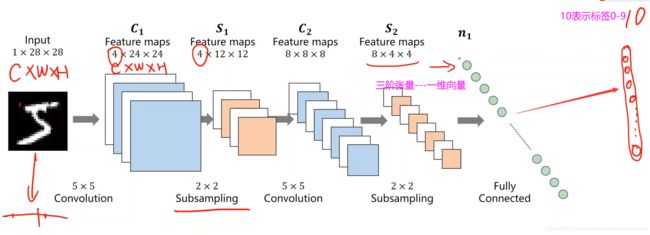
如上图，又经过了卷积和下采样，针对MNIST数据集，最注重输出的是图像对应所属10个分类的概率，所以最后要把8*4*4的三阶张量展开成一个一维的向量，可以用上一讲里面的view来实现，8个通道，每个通道有4*4个元素，按照某种顺序，把它展开成一维向量 ,如下图
展开之后就得到了线性的只有向量的输入，再用全连接层最终把这个向量映射到10维的输出，然后接上交叉熵损失利用softmax计算概率分布,解决分类问题

 

神经网络里面，卷积和下采样叫做特征提取器，能通过卷积运算，找到某种特征

分类器：经过特征提取之后把它变成向量，然后把这个向量连接全连接网络做分类 

图像到底是什么？

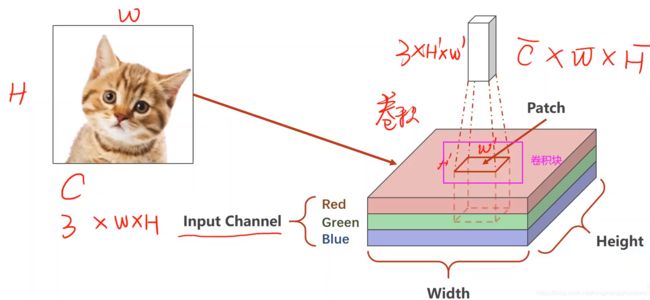
一般是用RGB三个通道表示的，如下图，每一个图像可以划分成很多个格子，给每一个格子填上颜色值就构成一个图像，叫做栅格图像，基本上从自然界获取图像都是采用这样的方式
图像如果放大就是一个一个的格子

相机拍照时，是通过传感器获得像素值，有红绿蓝三种颜色的传感器，传感器上有光敏电阻，电阻值与RGB值有对应关系，最终获得图像 

 

用这个卷积块把图像遍历一遍，然后对每一个块做卷积运算，得到卷积输出结果，最后把输出结果拼到一起，这就是卷积

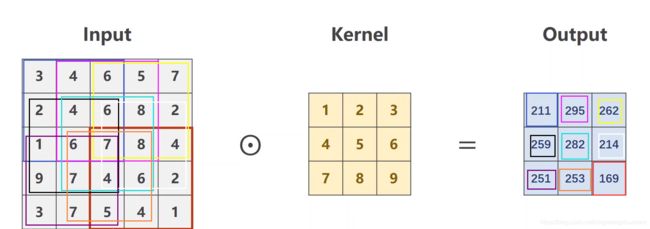
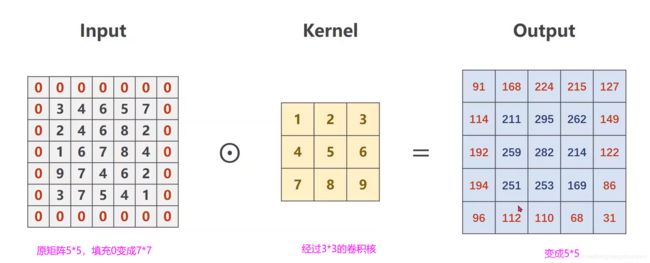
单通道图像卷积

 

如上图，输入是1*5*5的图像，卷积核是3*3，步长为1，经过卷积核在输入矩阵上运算（计算方式如上图）得到了13*3的输出，以上是单通道的卷积运算方法

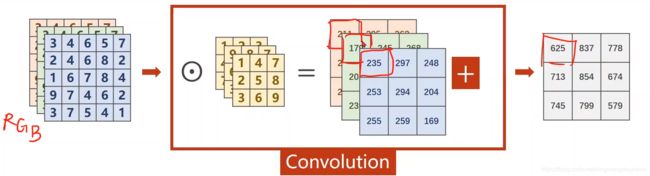
多通道卷积

    比如输入图像是3个通道，到神经网络中间的时候输入通道不一定是3个，几百个通道都有可能，以3通道为例，每一个通道都要配一个核，输入通道的数量与核的数量是一样的
如下图，三个通道分别和卷积核做卷积，得到3个矩阵，然后相加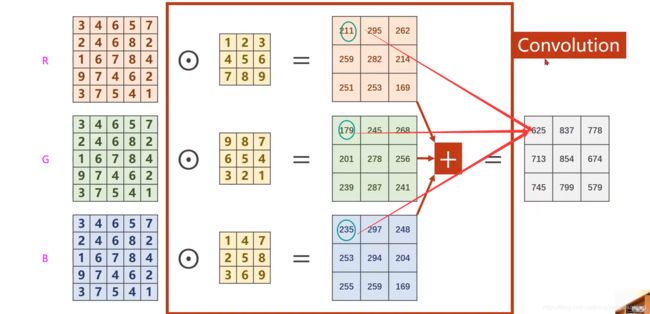

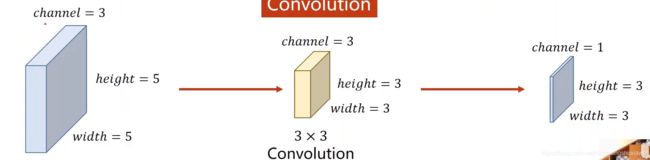
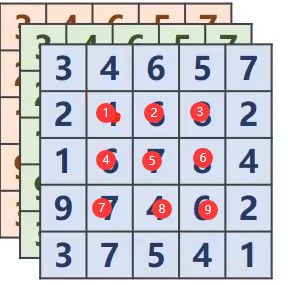
为什么输出的宽度和高度是3呢？ 

 我们看每一次卷积的中心

如果是3*3的卷积核，宽高是会减2的，上下左右各减一个 ；如果是5*5的卷积核，宽高减4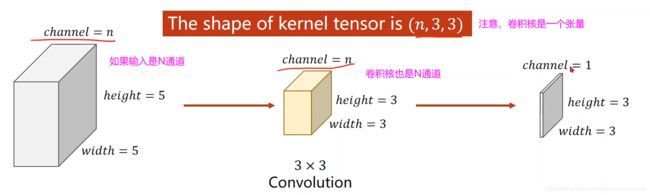

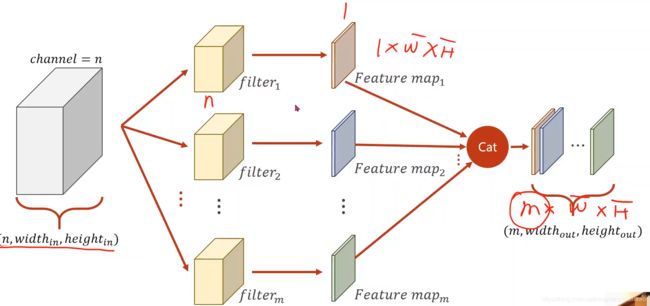
如果想要输出是m个通道怎么办呢？

 那就准备m个卷积核，每一个卷积核对原始输入卷积完之后通道数都是1，然后把这些通道拼接起来
每一个卷积核通道数量要求和输入通道一样
卷积核的数量和输出通道数是一样的
卷积核的大小自己定，与图像大小无关
共享权重机制：对每一个图像块操作用的是相同的卷积核

 可以把m个卷积核拼成4维张量 m(卷积核个数)*n（输入通道数）width* height，我们构建卷积层，它的权重就是这样的一个维度 

 所以定义一个卷积层，需要知道：输入通道数，输出通道数，卷积核大小

#卷积层并不在于输入的张量的宽度和高度，因为我们是复用的权重，只是把图像遍历一遍，图像大输出就大，图像小，输出就小
#所以卷积层对输入图像的宽度和高度没有要求，只对输入通道数有要求

import torch
in_channels,out_channels=5,10#n,m
width,height=100,100#图像的大小
kernel_size=3#卷积核的大小3*3
batch_size=1#pytorch里面所有输入的数据必须是小批量的数据
input=torch.randn(batch_size,
                  in_channels,
                  width,
                  height)#batch_size表示小批量的第几个
#torch.randn 生成输入数据的时候取的随机数，服从正态分布采样的随机数
conv_layer=torch.nn.Conv2d(in_channels,
                           out_channels,
                           kernel_size=kernel_size)
#Conv2d，卷积核也可以用长方形的，kernel_size=(5,3)
output=conv_layer(input)#把输入传进卷积层，得到输出
print(input.shape)#[1,5,100,100]
print(output.shape)#[1,10,98,98]
print(conv_layer.weight.shape)#卷积层权重的形状[10,5,3,3],10是输出通道的数量，5是输入通道的数量，3,3是卷积核的大小
#定义一个卷积层，需要确定输入通道，输出通道，卷积核的大小

 输出结果：

torch.Size([1, 5, 100, 100])
torch.Size([1, 10, 98, 98])
torch.Size([10, 5, 3, 3])

怎么保证卷积之后图像宽高不变？

这是有规律可循的
如果卷积核是3*3,3/2=1----->在原矩阵外补1圈0 padding=1
如果卷积核是5*5,5/2=2----->在原矩阵外补2圈0 padding=2

import torch
input=[3,4,6,5,7,
       2,4,6,8,2,
       1,6,7,8,4,
       9,7,4,6,2,
       3,7,5,4,1]
input=torch.Tensor(input).view(1,1,5,5)#把输入变成（batch_size,channel,width,height）
conv_layer=torch.nn.Conv2d(1,1,kernel_size=3,padding=1,bias=False)
#构建卷积层，输入是1个通道，输出是一个通道，卷积核3*3，如果bias=True,卷积完之后会给每一个通道加上一个偏置量
#不需要加偏置量就bias=False，padding=1是当卷积核为3*3时，保证输出还是5*5
kernel=torch.Tensor([1,2,3,4,5,6,7,8,9]).view(1,1,3,3)#构建卷积核（输出通道数，输入通道数，宽度，高度）
conv_layer.weight.data=kernel.data#把做出来的kernel张量的data赋值给卷积层的权重.data,把卷积层的权重初始化
output=conv_layer(input)
print(output)

结果

tensor([[[[ 91., 168., 224., 215., 127.],
          [114., 211., 295., 262., 149.],
          [192., 259., 282., 214., 122.],
          [194., 251., 253., 169.,  86.],
          [ 96., 112., 110.,  68.,  31.]]]],

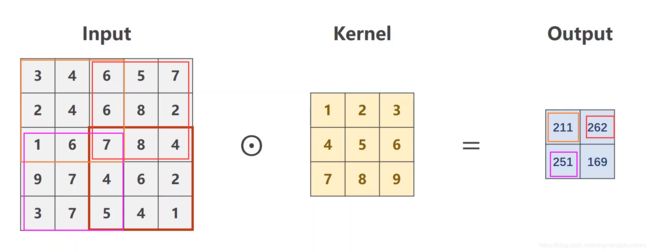
当步长stride=2 ：

 

 下采样

下采样用的比较多的是MaxPooling(最大池化层)
最大池化层是没有权重的
22的maxpooling默认stride=2
就是把图像分成22的一个组，在每个组里面找最大值
所以做maxpooling的时候只能把一个通道拿出来做maxpooling，通道之间不会去找最大值，所以在做最大池化（maxpooling）的时候，通道数量不会发生改变，但是如果用2*2的maxpooling,图像大小会缩成原来的一半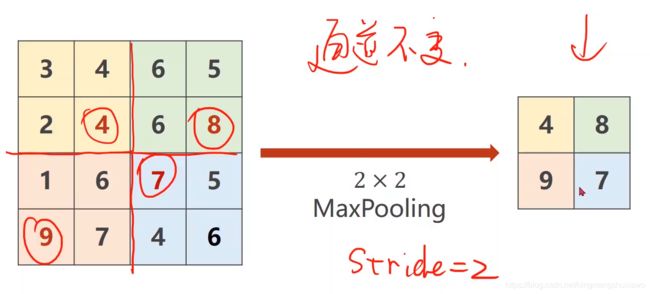

import torch
input=[3,4,5,6,
       2,4,6,8,
       1,6,7,8,
       9,7,4,6]
input=torch.Tensor(input).view(1,1,4,4)
maxpooling_layer=torch.nn.MaxPool2d(kernel_size=2)
#当kernel_size=2，maxpooling默认的步长也会是2
output=maxpooling_layer(input)
print(output)

 结果：

tensor([[[[4., 8.],
          [9., 8.]]]])

卷积神经网络实现MNIST

第一个最大池化做一个就行了，因为它没有权重，跟sigmoid和relu一样，是没有权重的，但是有权重的必须每一个层单独做一个实例 

参考代码：

import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F  # 用Relu函数
import torch.optim as optim  # 优化器优化

batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])
# transform：把图像转化成图像张量
train_dataset = datasets.MNIST(root='../dataset/mnist',
                               train=True,
                               download=True,
                               transform=transform)  # 训练数据集
train_loader = DataLoader(train_dataset,
                          shuffle=True,
                          batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist',
                              train=False,
                              download=True,
                              transform=transform)
test_loader = DataLoader(test_dataset,
                         shuffle=False,
                         batch_size=batch_size)


class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = torch.nn.Conv2d(1,10,kernel_size=5)
        self.conv2 = torch.nn.Conv2d(10,20,kernel_size=5)
        self.pooling = torch.nn.MaxPool2d(2)
        self.fc = torch.nn.Linear(320,10)

    def forward(self, x):
        batch_size = x.size(0)
        x = F.relu(self.pooling(self.conv1(x)))
        x = F.relu(self.pooling(self.conv2(x)))
        # Flatten data from (n,1,28,28) to (n,784) Flatten层用来将输入“压平”，即把多维的输入一维化，常用在从卷积层到全连接层的过渡。
        x = x.view(batch_size,-1)
        x = self.fc(x)  #x应用全连接网络
        return x

model = Net()
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)


# 因为网络模型已经有点大了，所以梯度下降里面要用更好的优化算法，比如用带冲量的（momentum），来优化训练过程


# 把一轮循环封装到函数里面
def train(epoch):
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):
        inputs, target = data
        optimizer.zero_grad()  # 优化器，输入之前清零
        # forward + backward + updat
        outputs = model(inputs)
        loss = criterion(outputs, target)
        loss.backward()
        optimizer.step()
        running_loss += loss.item()
        if batch_idx % 300 == 299:  # 每300轮输出一次
            print('[%d,%5d] loss：%.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
            running_loss = 0.0


def test():
    correct = 0  # 正确多少
    total = 0  # 总数多少
    with torch.no_grad():  # 测试不用算梯度
        for data in test_loader:  # 从test_loader拿数据
            images, labels = data
            outputs = model(images)  # 拿完数据做预测
            _, predicted = torch.max(outputs.data, dim=1)  # 沿着第一个维度找最大值的下标，返回值有两个，因为是10列嘛，返回值
            # 返回值一个是每一行的最大值，另一个是最大值的下标（每一个样本就是一行，每一行有10个量）（行是第0个维度，列是第1个维度）
            total += labels.size(0)  # 取size元组的第0个元素（N，1），
            correct += (predicted == labels).sum().item()  # 推测出来的分类与label是否相等，真就是1，假就是0，求完和之后把标量拿出来
    print('Accuracy on test set:%d %%' % (100 * correct / total))


# 训练
if __name__ == '__main__':
    for epoch in range(10):
        train(epoch)
        test() #训练一轮，测试一轮

如果有GPU,怎么用显卡来计算

①把模型迁移到GPU

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu") 
model.to(device)

如果装的是支持cuda版本的pyTorch,available就是True，默认是cuda 0,只有cpu就是false
如果有多个显卡，不同的任务可以使用不同的显卡
model.to(device)把整个模型的参数，缓存，所有的模块都放到cuda里面，转成cuda tensor

 计算的时候要把用来计算的张量也迁移到GPU，主要是输入和对应的输出，把inputs和target都迁移到device上，注意迁移的device和模型的device要在同一块显卡上，比如把模型放在第0块显卡，数据放在第一块显卡，是没法工作的

inputs, target = inputs.to(device), target.to(device) 

测试也把输入输出放到显卡上

view()函数
参考文章：https://blog.csdn.net/ningmengshuxiawo/article/details/108356453

补充知识：CNN基础知识——卷积（Convolution）、填充（Padding）、步长(Stride) - 知乎