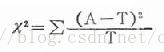卡方检验特征选择
参考:
https://segmentfault.com/a/1190000003719712
http://blog.csdn.net/shuzfan/article/details/52993427
卡方检验,或称x2检验,是一种常用的特征选择方法,尤其是在生物和金融领域。 χ2 用来描述两个事件的独立性或者说描述实际观察值与期望值的偏离程度。 χ2 值越大,则表明实际观察值与期望值偏离越大,也说明两个事件的相互独立性越弱。
无关性假设
【例1】举个例子,假设我们有一堆新闻标题,需要判断标题中包含某个词(比如吴亦凡)是否与该条新闻的类别归属(比如娱乐)是否有关,我们只需要简单统计就可以获得这样的一个四格表:
| 组别 | 属于娱乐 |
不属于娱乐 |
合计 | |
|---|---|---|---|---|
不包含吴亦凡 |
19 | 24 | 43 | |
包含吴亦凡 |
34 | 10 | 44 | |
| 合计 | 53 | 34 | 87 |
通过这个四格表我们得到的第一个信息是:标题是否包含吴亦凡确实对新闻是否属于娱乐有统计上的差别,包含吴亦凡的新闻属于娱乐的比例更高,但我们还无法排除这个差别是否由于抽样误差导致。那么首先假设标题是否包含吴亦凡与新闻是否属于娱乐是独立无关的,随机抽取一条新闻标题,属于娱乐类别的概率是:(19 + 34) / (19 + 34 + 24 +10) = 60.9%
理论值四格表
第二步,根据无关性假设生成新的理论值四格表:
| 组别 | 属于娱乐 |
不属于娱乐 |
合计 |
|---|---|---|---|
不包含吴亦凡 |
43 * 0.609 = 26.2 | 43 * 0.391 = 16.8 | 43 |
包含吴亦凡 |
44 * 0.609 = 26.8 | 44 * 0.391 = 17.2 | 44 |
显然,如果两个变量是独立无关的,那么四格表中的理论值与实际值的差异会非常小。
x2值的计算
x2的计算公式为:
其中A为实际值,也就是第一个四格表里的4个数据,T为理论值,也就是理论值四格表里的4个数据。
x2用于衡量实际值与理论值的差异程度(也就是卡方检验的核心思想),包含了以下两个信息:
-
实际值与理论值偏差的绝对大小(由于平方的存在,差异是被放大的)
-
差异程度与理论值的相对大小
对上述场景可计算x2值为10.01。
卡方分布的临界值
既然已经得到了x2值,我们又怎么知道x2值是否合理?也就是说,怎么知道无关性假设是否可靠?答案是,通过查询卡方分布的临界值表。
这里需要用到一个自由度的概念,自由度等于V = (行数 - 1) * (列数 - 1),对四格表,自由度V = 1。
对V = 1,卡方分布的临界概率是:
显然10.01 > 7.88,也就是标题是否包含吴亦凡与新闻是否属于娱乐无关的可能性小于0.5%,反过来,就是两者相关的概率大于99.5%。
【例2】
比如我们现在有一个生物学问题,我们需要从采样的5个基因 gene1,…,gene5 中找到某种疾病的1个致病基因。下表我们分别统计了患病和不患病人群5种基因的出现频率。当我们把一种基因看做一种特征的时候,找到致病基因就可以看做是选择一种特征使得患病-不患病的二分类问题准确率最高。
| gene1 | gene2 | gene3 | gene4 | gene5 |
|---|---|---|---|---|
| 患病 | 0.73 | 0.24 | 0.21 | 0.54 |
| 不患病 | 0.71 | 0.26 | 0.87 | 0.55 |
首先,我们做出假设 “患病与gene_x无关”。
以gene1为例,分布比较稳定, χ2 值应该比较小,即两事件相互独立性比较强,即假设成立。
再以gene3为例,分布偏差很大, χ2 值应该很大,即两事件相互独立性很弱,即假设不成立,因此最后我们选择gene3作为致病基因。
上述的例子比较简单,也存在一些不合常理的地方,仅仅用于帮助大家理解。
———————— 计算 χ2 值 ————————
接下来我们讲怎样具体地计算 χ2 值。
先直接上公式:
X2(t,c)=∑et∈0,1∑ec∈0,1(Netec−Eetec)2Eetec
其中 t:term ,即某个特征有或无, c:class ,即类别1或0(这里只支持2分类)。 N 是观察值, E 是期望值。则 E11 表示出现特征 t 且 类别 c=1 。
现在,我们以第一节中的 gene3 为例,来计算 χ2 值,当然按照公式我们首先应该计算各种期望和观测值。首先,我们来虚构一个完整的患病-基因数据集。假如我们记录了10个人的gene3出现情况,得到类似于下面的表格:
| 样本编号 | gene3是否出现 | 是否患病 |
|---|---|---|
| 1 | 1 | 0 |
| 2 | 1 | 0 |
| 3 | 1 | 1 |
| 4 | 1 | 0 |
| 5 | 1 | 0 |
| 6 | 0 | 1 |
| 7 | 1 | 0 |
| 8 | 0 | 1 |
| 9 | 1 | 0 |
| 10 | 0 | 1 |
据此我们可以很容易的计算所有的观测值以及期望值。
首先是观测值
N11=患病且出现gene3的人数=1
N01=患病且不出现gene3的人数=3
N10=不患病出现gene3的人数=6
N00=不患病不出现gene3的人数=0
然后是期望值:(因为我们的假设是t和c独立,因此可以直接按照下式计算)
E11=10×P(t=1)×P(c=1)=2.8
N01=10×P(t=0)×P(c=1)=1.2
N10=10×P(t=1)×P(c=0)=4.2
N00=10×P(t=0)×P(c=0)=1.8
代入公式有:
X2(t,c)=(1−2.8)22.8+(3−1.2)21.2+(6−4.2)24.2+(0−1.8)21.8=6.4286
我们已经得到了 χ2 值,但是这并不够直接明了的说明问题。因此,我们还需要将 χ2 值转化为 p-value。p-value是一种给定原假设为真时样本结果出现的概率,我们可以通过简单查表来进行转化。如下表:自由度=1时的转化表格。(自由度=分类数-1,因此这里自由度=1.)
| p-value | χ2 |
|---|---|
| 0.1 | 2.71 |
| 0.05 | 3.84 |
| 0.01 | 6.63 |
| 0.005 | 7.88 |
| 0.001 | 10.83 |
我们的 χ2 值为6.4286,转化为p-value约为0.01,意思是假设患病和gene3无关的情况下,只有约0.01的概率会出现这样的样本结果。因此,我们就有约0.99的概率认为原假设错误,则gene3与患病有关。
应用场景
卡方检验的一个典型应用场景是衡量特定条件下的分布是否与理论分布一致,比如:特定用户某项指标的分布与大盘的分布是否差异很大,这时通过临界概率可以合理又科学的筛选异常用户。
另外,x2值描述了自变量与因变量之间的相关程度:x2值越大,相关程度也越大,所以很自然的可以利用x2值来做降维,保留相关程度大的变量。再回到刚才新闻分类的场景,如果我们希望获取和娱乐类别相关性最强的100个词,以后就按照标题是否包含这100个词来确定新闻是否归属于娱乐类,怎么做?很简单,对娱乐类新闻标题所包含的每个词按上述步骤计算x2值,然后按x2值排序,取x2值最大的100个词。