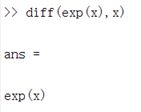数值分析：利用牛顿法解非线性方程组的matlab和python实现

问题描述

例如对     这个非线性方程组使用牛顿法进行求解，且设初始值为x0 = （1.6，1.2）T。

 

计算机实现牛顿法基本思路

 

直接用fsolve函数求解

对于非线性方程组F(X)=0，用fsolve函数求其数值解。fsolve函数的调用格式为：

X=fsolve('fun',X0,option)

其中X为返回的解，fun是用于定义需求解的非线性方程组的函数文件名，X0是求根过程的初值，option为最优化工具箱的选项设定。最优化工具箱提供了20多个选项，用户可以使用optimset命令将它们显示出来。如果想改变其中某个选项，则可以调用optimset()函数来完成。例如，Display选项决定函数调用时中间结果的显示方式，其中‘off’为不显示，‘iter’表示每步都显示，‘final’只显示最终结果。optimset(‘Display’,‘off’)将设定Display选项为‘off’。

例如：

关于数值分析的几个重要的函数

在编写代码前先熟悉下写牛顿法时需要用到的几个函数。

Syms定义符号变量

syms就是定义一些符号变量，用来进行符号运算用的。

例如，当我们想直接写出F(x) = x^2 + 1这个表达式时。Matlab会显示：

于是，我们要事先声明x是一个自变量：syms x。

这样，我们再次输入表达式时，就变成了这样：

当然，也可以同时赋好几个自变量：

Subs表达式求值

subs()是符号计算函数，表示将符号表达式中的某些符号变量替换为指定的新的变量，常用调用方式为：

subs(S,OLD,NEW) 表示将符号表达式S中的符号变量OLD替换为新的值NEW。

例如对F = x^2 + 1这个表达式求x = 2时的值：

也可以将此时的自变量x换为自变量y：

同时将多个自变量赋值时，就像这样：

Diff求导

diff函数可用于求导或求差分。

以F = x^2 + y^3为例，对其求偏导：

对y = e^x 求导则是这样的：

利用matlab实现牛顿迭代法

syms x1 x2;

f1 = x1^2 + x2^2 - 4;

f2 = x1^2 - x2^2 - 1;

F = [f1;f2];

F_ = [diff(f1,x1),diff(f1,x2);diff(f2,x1),diff(f2,x2)];%求出雅可比矩阵

F__ = inv(F_);%求出雅可比矩阵的逆矩阵

x0 = [1.6;1.2];%设置初始值

for i = 1:5%循环5次

ff = x0 - F__*F;

x0 = subs(ff,{x1,x2},{x0.'});

sprintf('第%d次迭代所得值为%f和%f',[i,x0(1),x0(2)])

end

运行结果为：

利用python实现牛顿迭代法

from sympy import *
import numpy as np
import math

#设置方程组
e = math.e
x1 = symbols('x1')
x2 = symbols('x2')
f1 = x1**2 + x2**2 - 4
f2 = x1**2 - x2**2 - 1

#F_为F的导数的逆矩阵
a,b,c,d = diff(f1,x1),diff(f1,x2),diff(f2,x1),diff(f2,x2)
a,b,c,d = [x/(a*d-b*c) for x in [d,-b,-c,a]]
F = np.array([[f1],[f2]])
F_ = np.array([[a,b],[c,d]])

#设置初始值
init_value = np.array([1.6,1.2])
for i in range(5):
    k1,k2 = init_value
    ff1,ff2 = np.array([[k1],[k2]]) - np.dot(F_,F)
    ff1,ff2 = list(ff1)[0],list(ff2)[0]
    k_1,k_2 = ff1.subs([(x1,k1),(x2,k2)]),ff2.subs([(x1,k1),(x2,k2)])
    init_value = np.array([k_1,k_2])
    print('第%d次迭代：'%(i+1),'x1=',k_1,'x2=',k_2)

输出结果为：

第1次迭代： x1= 1.58125000000000 x2= 1.22500000000000
第2次迭代： x1= 1.58113883399209 x2= 1.22474489795918
第3次迭代： x1= 1.58113883008419 x2= 1.22474487139159
第4次迭代： x1= 1.58113883008419 x2= 1.22474487139159
第5次迭代： x1= 1.58113883008419 x2= 1.22474487139159