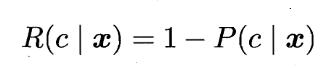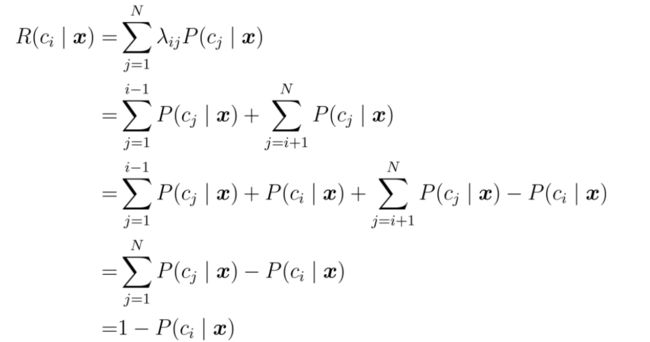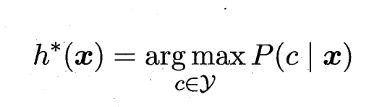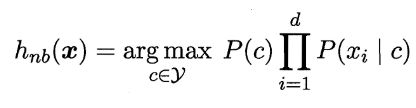朴素贝叶斯分类器_机器学习——朴素贝叶斯分类器
贝叶斯定理：
先验概率：是指根据以往经验和分析得到的概率
例：如果我们对西瓜的色泽、根蒂和纹理等特征一无所知，按照常理来说，西瓜是好瓜的概率是60%。那么这个概率P(好瓜)就被称为先验概率
后验概率：事情已经发生，要求这件事情发生的原因是由某个因素引起的可能性的大小
例：假如我们了解到判断西瓜是否好瓜的一个指标是纹理。一般来说，纹理清晰的西瓜是好瓜的概率大一些，大概是75%。如果把纹理清晰当作一种结果，然后去推测好瓜的概率，那么这个概率P(好瓜|纹理清晰)就被称为后验概率。后验概率类似于条件概率
联合概率：包含多个条件且所有条件同时成立的概率，记作 P(X=i,Y=j)，或记作 P(i,j)
例：在买西瓜的案例中，P(好瓜，纹理清晰)称为联合分布，它表示纹理清晰且是好瓜的概率，计算方法如下：
全概率：如果事件组B1,B2......满足：
例：上面联合概率概念买西瓜的例子中，我们要计算P(好瓜，纹理清晰)联合概率时，需要知道P(纹理清晰)的概率。那么，如何计算纹理清晰的概率呢？实际上可以分为两种情况：一种是好瓜状态下纹理清晰的概率，另一类是坏瓜状态下纹理清晰的概率。纹理清晰的概率就是这两种情况之和。因此，我们可以推导出全概率公式：
贝叶斯定理：贝叶斯公式是建立在条件概率的基础上寻找事件发生的原因(即大事件A已经发生的条件下，分割中的小事件Bi的概率)，设B1,B2…是样本空间Ω的一个划分，则对任一事件A(P(A)>0)，有贝叶斯定理： 
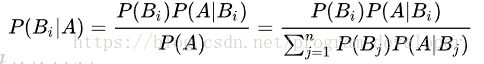对于每个特征x，我们想要知道样本在这个特性x下属于哪个类别，即求后验概率 P(c|x) 最大的类标记。这样基于贝叶斯公式，可以得到： 
贝叶斯决策论：
假设有 N 种可能的类别标记，即 y = { c1 , c2 , c3 ... cN }，λij 是将一个真实标记为 cj 的样本误分类为 ci 所产生的损失。基于后验概率 P(ci|x) 可获得将样本分类为 ci 所产生的期望损失，即在样本 x 上的“条件风险”：
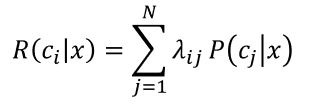
等号左侧表示将样本 x 分类为 ci 所产生的期望损失，也就是说，现在已知样本被分类为 ci，想知道这一事实的期望损失是多少
那么，根据样本 x 真实类别标记的不同，x 被分类为 ci 所产生的损失也不同，当样本 x 真实类别标记为 c1 时，误分类为 ci 所产生的损失为λi1，当样本 x 真实类别标记为 c2 时，误分类为 ci 所产生的损失为λi2，......，当样本 x 真实类别标记为 cj 时，误分类为 ci 所产生的损失为λij，......
因此，只要知道样本 x 真实类别标记，就可以知道将其分类为 ci 所产生的损失，现在待求的条件风险 R(ci|x) 是将样本 x 分类为 ci 所产生的期望损失，即所有损失的平均值，其中，x 标记为 cj 的概率为 P(cj|x)，即 已知 x 的情况下，类别标记为cj的后验概率
x 是针对单个样本的，对于数据集 D 所有样本点期望为：
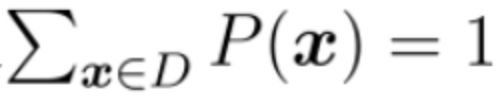； h(x)为判定准则，其中 
表示对 样本 x 预测的类别标记； 则 R(h) 表示判定准则的总体风险
对每个样本 x，若 h 能最小化条件风险 R(h(x)|x)，则总体风险 R(h) 也将被最小化
贝叶斯准则：为最小化总体风险，只需在每个样本上选择那个能使条件风险 R(c|x) 最小的类别标记，即：
此时，h* 被称为贝叶斯最优分类器，R(h*) 被称为贝叶斯风险，1 - R(h*) 反映了贝叶斯分类器所能达到的最好性能
误判损失 λij 可写为：
此时条件风险：
推导：
于是，最小化分类错误率的贝叶斯最优分类器为：
朴素贝叶斯分类器：
由于类条件概率 P(x|c) 是所有属性上的联合概率，计算困难，朴素贝叶斯分类器采用了“属性条件独立性假设”，对于已知类别，假设所有属性相互独立，即每个属性独立地对分类结果发生影响，则有：
其中，d 为属性数目，xi 为 x 在第 i 个属性上的取值
由于对于所有类别来说 P(x) 相同，根据贝叶斯判定准则，有：
基于训练集D可以估算出类先验概率 P(c) ，并为每个属性估计条件概率 P(xi|c)
在连续型模型中，假设概率密度函数
，则根据最大似然估计参数得：
举例说明：
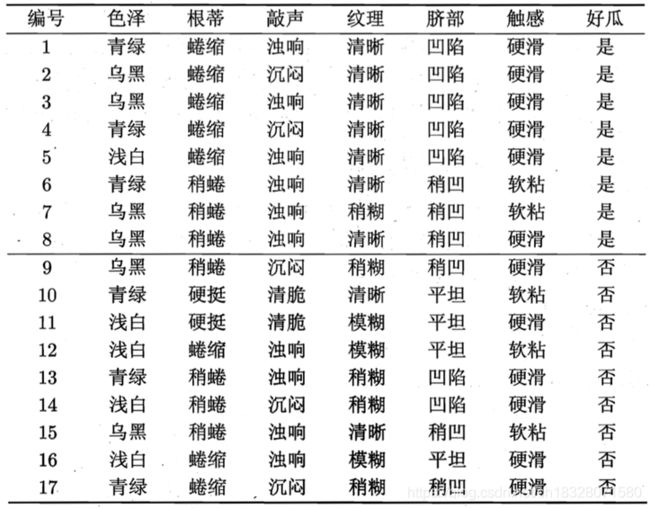
需注意，若某个属性值在训练集中没有与某个类同时出现过，例如“敲声=清脆”的测试例，则有：
为了避免，通常要进行“平滑”，拉普拉斯修正：
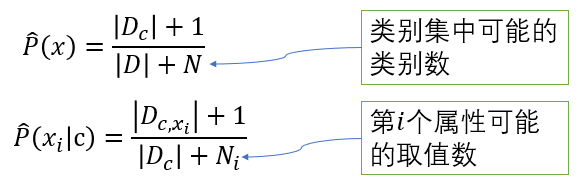
例如，在本节的例子中，类先验概率可估计为 :
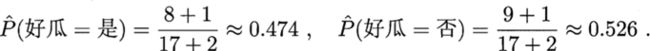
拉普拉斯修正避免了因训练集样本不充分而导致概率估值为零的问题