【深度学习】从self-attention到transformer(Multi-head self-attention)
#版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。本文链接:https://blog.csdn.net/weixin_43414694/article/details/119083072
该教程主要参考的是台大李宏毅的网课视频,附上视频链接:台大李宏毅self-attention教程
文中图片均引自台大李宏毅的PPT,需要PPT的童鞋请戳这里:教程配套PPT
本文针对视频中的一些重点进行总结,看不懂的童鞋还请去看原视频,毕竟李宏毅yyds!!
背景什么的就不再介绍了,网上一搜一大堆,不知道背景的童鞋可以先去度娘问一下。
简介
今天讲以self-attention为基础讲解它的升级版 Muti-head self-attention,不了解self-attention的童鞋可以戳这里【深度学习】从self-attention到transform(self-attention入坑指南)
废话不说,正式开始。
为什么要使用Multi-head self-attention?
单纯从字面意思看,Multi-head self-attention比self-attention多了Multi-head,它的意思为多头。可以理解为多种关系。在【深度学习】从self-attention到transform(self-attention入坑指南)
一文中我们提到,寻找两个输入向量 a 1 和 a 2 a^1和a^2 a1和a2之间的相关度 α 12 = q 1 k 2 \alpha_{12}=q_1k_2 α12=q1k2,这说明 a 1 和 a 2 a^1和a^2 a1和a2之间有一种关系,它的关系的强弱用参数 α 12 = q 1 k 2 \alpha_{12}=q_1k_2 α12=q1k2来衡量,那假如 a 1 和 a 2 a^1和a^2 a1和a2有两种关系甚至三种关系呢,使用一个 α 12 \alpha_{12} α12显然是不能衡量的,因此提出了Multi-head self-attention用来衡量输入向量之间的多种关系。本文以两种关系(也就是两个head)为例展开说明。
重点来了
既然有两种关系,那么输入向量 a i a^i ai对应的 q , k , v q, k, v q,k,v就不只有一个了(在普通的self-attention中,每个输入向量都有一个 q , k , v q, k, v q,k,v与之对应),而是有两个(有多少个head一个输入向量就对应有几个 q , k , v q, k,v q,k,v),这里我们用 q i 1 , q i 2 , k i 1 , k i 2 , v i 1 , v i 2 q^{i1}, q^{i2}, k^{i1}, k^{i2}, v^{i1}, v^{i2} qi1,qi2,ki1,ki2,vi1,vi2表示,其中 q i l = W q l q i ( l = 1 , 2 ) q^{il}=W^{ql}q^i (l=1,2) qil=Wqlqi(l=1,2) k i l = W k l k i ( l = 1 , 2 ) k^{il}=W^{kl}k^i (l=1,2) kil=Wklki(l=1,2) v i l = W v l q i ( l = 1 , 2 ) v^{il}=W^{vl}q^i (l=1,2) vil=Wvlqi(l=1,2)
同理对于另一个输入向量 a j a_j aj,也有两个 q , k , v q, k, v q,k,v与之对应 q j 1 , q j 2 , k j 1 , k j 2 , v j 1 , v j 2 q^{j1}, q^{j2}, k^{j1}, k^{j2}, v^{j1}, v^{j2} qj1,qj2,kj1,kj2,vj1,vj2表示,其中 q j l = W q l q j ( l = 1 , 2 ) q^{jl}=W^{ql}q^j (l=1,2) qjl=Wqlqj(l=1,2) k j l = W k l k j ( l = 1 , 2 ) k^{jl}=W^{kl}k^j (l=1,2) kjl=Wklkj(l=1,2) v j l = W v l q j ( l = 1 , 2 ) v^{jl}=W^{vl}q^j (l=1,2) vjl=Wvlqj(l=1,2) 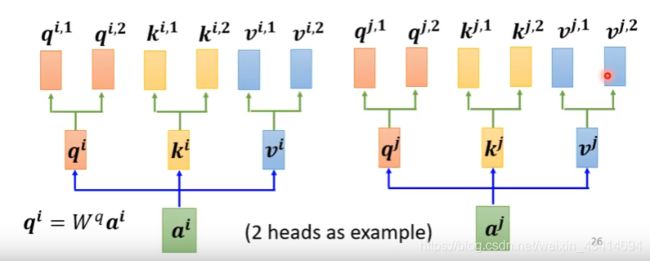
下面开始计算相关度 α \alpha α
在self-attention中,两个输入向量的相关度的求解公式为 α i j = q i ⋅ k j \alpha_{ij}=q_i \centerdot k_j αij=qi⋅kj,而在Multi-head self-attention中,相关度的计算需要根据head进行。也就是说第一个head之间的有一个相关度,第二个head之间也就一个相关度。根据上图,head1上的相关度 α i j 1 = q i 1 ⋅ k j 1 + q i 1 ⋅ k i 1 \alpha^1_{ij}=q^{i1} \centerdot k^{j1} + q^{i1} \centerdot k^{i1} αij1=qi1⋅kj1+qi1⋅ki1,head2上的相关度 α i j 2 = q i 2 ⋅ k j 2 + q i 2 ⋅ k i 2 \alpha^2_{ij}=q^{i2} \centerdot k^{j2} + q^{i2} \centerdot k^{i2} αij2=qi2⋅kj2+qi2⋅ki2
根据相关度计算输出 b b b
self-attention的输出的计算公式为: b i = ∑ j α i j ′ v i b^i=\sum_j \alpha'_{ij} v_i bi=∑jαij′vi,其中 α i j ′ = s o f t m a x ( α i j ) \alpha'_{ij}=softmax(\alpha_{ij}) αij′=softmax(αij)。
在Multi-head self-attention中,b的计算同样需要根据head进行,即 b i 1 = v i 1 α i j 1 b^{i1}=v_{i1} \alpha^1_{ij} bi1=vi1αij1 b i 2 = v i 2 α i j 2 b^{i2}=v_{i2} \alpha^2_{ij} bi2=vi2αij2 最后将 b i 1 和 b i 2 拼 接 起 来 并 乘 一 个 输 出 矩 阵 W O 就 可 以 得 到 最 终 的 输 出 b b^{i1}和b^{i2}拼接起来并乘一个输出矩阵W^O就可以得到最终的输出b bi1和bi2拼接起来并乘一个输出矩阵WO就可以得到最终的输出b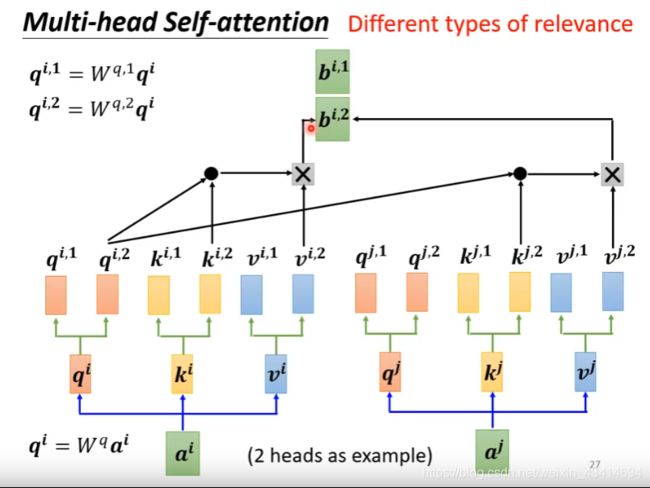

以上就是Multi-head self-attention基本内容,如果理解了self-attention的话,理解这个还是比较容易的,Multi-head self-attention就相当于多重复了几遍self-attention。
下一篇我们就开始正式进入transformer的讲解。