【机器学习杂记】自注意力机制(Self-attention)
初学self-attention,是学习笔记,基于李宏毅老师的课程。有缘人看到的话若有错误的不完善的地方还请指出,不胜感激!
\space
零 引出
有时候我们的模型具有复杂的输入,例如不定长的向量集合。例如语音识别、机器翻译等任务,其输入是不定长的。
在这种应用背景下,输出有两种:
- 一是每个输入向量都有一个对应的输出,例如词性判(POS
tagging);对于一个graph,决定每个节点的特性(例如根据一个社交网络做个性化推荐) - 二是一整个输入的sequence只对应一个输出的label,例如情感判别
- 三是不知道输出多少个label,由model自己决定 (这种任务称作seq2seq任务),例如输入为语音信号,输出为识别文字
先学第一种输入输出数目一样的情况。这种情形又叫做Sequence Labeling。
由于输入的向量之间是有关联的,因此不能逐个独立地考虑,这就是self-attention发挥作用的地方。其也是Transformer里重要的组成部分。
\space
一 Sequence Labeling的计算方式
\space
1.1 基本原理
\space
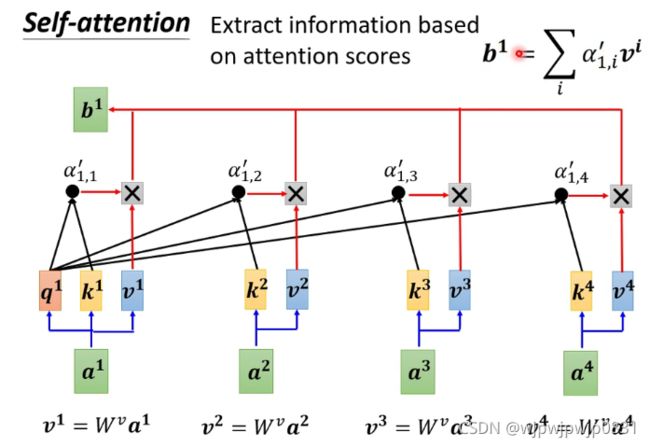
图中最底部的四个向量代表输入向量,中间经过Self-attention的框架(下文讲),输出与输入个数相同的向量。Self-attention输出的向量已经包含了上下文信息,这些包含上下文信息的新向量可以经过全连接层计算出结果。
注意: 在一个框架中可以用多次Self-attention。
\space
具体Self-attention是怎么运作的呢?
最核心的思想就是: 通过一些经过训练的矩阵来计算输入向量之间的相关性。具体地:
1.Dot product方法: 对于两个向量 a 1 , a 2 a^1,a^2 a1,a2,若要计算二者的相关性,将其分别乘两个不同的矩阵得到两个向量: q = W q a 1 , k = W k a 2 q=W_qa^1,k=W_ka^2 q=Wqa1,k=Wka2,再计算 q , k q,k q,k的内积: α 1 , 2 = ( q , k ) \alpha_{1,2}=(q,k) α1,2=(q,k), α \alpha α就衡量了相关程度,框图如下:
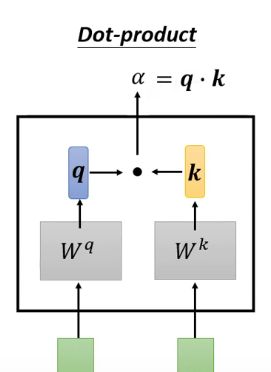
这里, q q q有个名字叫query, k k k有个名字叫key, α \alpha α叫attention score。
2.Additive方法: Additive比Dot product多了一些运算,框图如下:

下面的说明都是基于Dot product方法的。
因此,假如我们输入了四个向量,则attention score的计算方法如下:

注意: 看图得出,计算某一个向量与其他向量关联性的时候,也要计算自己和自己的关联性( α i , i = ( q i , k i ) \alpha_{i,i}=(q^i,k^i) αi,i=(qi,ki)),计算出 α i , j \alpha_{i,j} αi,j后再经过一个softmax层(换别的也行,例如ReLU)。
接下来要做的就是从计算出的attention score里提取信息。这时我们需要一个新的矩阵 W v W^v Wv,输入向量与 W v W^v Wv相乘后得到的向量计算加权和,权重就是之前计算出的attention score。框图:
b i = ∑ j α i , j ′ v j , v j = W v α j b_i=\sum_{j}\alpha'_{i,j}v^j,\space \quad v^j=W^v\alpha^j bi=j∑αi,j′vj, vj=Wvαj
b i b_i bi就反映了第 i i i个input和其余input的相关程度。
(一个疑问: 所有的input都共享同样的矩阵吗?感觉很怪。感觉为每个input都训练特别的矩阵也没啥)
\space
1.2 矩阵表达
在实际中肯定是并行计算的,所以我们找到简洁的矩阵表达形式就尤为重要。
假设有 N N N个输入 a 1 , . . . , a N a^1,...,a^N a1,...,aN,query的计算可表示为:
[ q 1 , q 2 , . . . , q N ] = W q [ a 1 , a 2 , . . . , a N ] [q^1,q^2,...,q^N]=W^q[a^1,a^2,...,a^N] [q1,q2,...,qN]=Wq[a1,a2,...,aN]
写成:
Q = W q I Q=W^qI Q=WqI
同理:
K = [ k 1 , . . . , k N ] = W k [ a 1 , a 2 , . . . , a N ] = W k I K=[k^1,...,k^N]=W^k[a^1,a^2,...,a^N]=W^kI K=[k1,...,kN]=Wk[a1,a2,...,aN]=WkI
attention score的计算:
A = [ α i , j ] N × N = K T Q A=[\alpha_{i,j}]_{N\times N}=K^TQ A=[αi,j]N×N=KTQ
别忘了还要经过一层激活函数,假设表示成 σ \sigma σ,最终的attention score矩阵:
A ′ = σ ( A ) A'=\sigma(A) A′=σ(A)
最终的那个 b b b:
O = [ b 1 , . . . , b N ] = [ v 1 , . . . , v N ] A ′ O=[b^1,...,b^N]=[v^1,...,v^N]A' O=[b1,...,bN]=[v1,...,vN]A′
O O O就是Self-attention计算出的输出了。把上面的过程形象化一点就是下面这个图:
\space
二 Multi-head Self-attention
所谓Multi-head,就是在计算出 q q q, k k k和 v v v向量的基础上,再加一层,将 q q q, k k k和 v v v向量分出多个头来,当然在计算 b b b的时候,也是根据每个head算出 b i b_i bi,再算一个总的 b b b。
例如,对于head=2的情形,框图如下:

\space
最后根据 b i , 1 b^{i,1} bi,1和 b i , 2 b^{i,2} bi,2算出 b i b^i bi:
b i = W O [ b i , 1 , b i , 2 ] T b^i=W^O[b^{i,1},b^{i,2}]^T bi=WO[bi,1,bi,2]T
我觉得 W O W^O WO的shape应该是 ( n ⋅ h e a d , n ⋅ h e a d ) (n·head,n·head) (n⋅head,n⋅head),其中 n n n应该是输入向量的维度,head是头的数目。
\space
三 Positional Encoding
可以看出,前面的架构其实并没有考虑到输入向量的位置信息,实际上它们的位置都是等价的。如果对于NLP的任务来说,显然词汇的位置是很重要的。因此要把位置编码的信息加入到输入向量当中去,方法有很多,比如对于位置 i i i定义一个位置向量 e i e^i ei,那么输入的向量为:
e i + n i e^i+n^i ei+ni
e i e^i ei的定义方式多种多样,也是一个研究热点之一。
\space
四 Self-attention跟CNN的关系
CNN有两种理解方式,一种是常见的从二维卷积的角度去理解。还有一种等价的理解方式,就是理解成权值共享的网络。可以将整张输入图片划分成多个receptive field,每一块receptive field都有等数量的neuron来负责,且对应neuron的权值都是共享的。
为什么说这两种对CNN的说法等价呢,因为拿一个kernel去卷积一幅图,不就是拿相同的权值去计算不同的receptive field(我的理解,不一定对)
从第二种角度看CNN,就可以看出来其和Self-attention有相通之处。实际上CNN是Self-attention的subset,可以看成是变形的Self-attention。
\space
五 Self-attention跟RNN的关系
RNN网络不能并行计算,也不能长时记忆,很后面的输入很难与很前面的输入产生关联,然而Self-attention没有这些问题。
好像,RNN要被抛弃了…
\space
六 Self-attention和图
图已经预设好了顶点和顶点之间的联系,所以在计算图的顶点之间相关度的时候,就没必要每个顶点之间都计算了。
有个小想法,可不可以把MOT里二部图匹配的任务和Self-attention挂上钩?当然只是瞎想,还没看论文呢…