pytorch9-权重衰减

权重衰减

这是一种常用的用于减轻过拟合的方法。

原理

我们以一下公式作为损失函数
$$l(w_1,w_2,b)=\frac{1}{n}\sum _{i=1}^n\frac{1}{2}(x_1^i{w}_1+x_2^i{w}_2+b-y^i{)}^2$$
以上公式$w_1$和$w_2$是权重，样本i的输入为$x_1^i,x_2^i$ ,偏差是$b$ ,样本标签为y^{i}.那么以上公式可以扩展为以下公式
$$L(w_1,w_2,b)+\frac{\lambda }{2n}||w|{|}^2$$
这里的超参量$\lambda >0$。这个$\lambda$决定了权重衰减的比重，当$\lambda =0$的时候，权重衰减就是无效的，当$\lambda$越大，权重衰减就完全不起作用了。
$$w_1\leftarrow (1-\frac{n\lambda }{|B|})w_1-\frac{n}{|B|}\sum _{i\in B}{x}_1^i(x_1^i{w}_1+x_2^i{w}_2+b-y^i)$$
$$w_2\leftarrow (1-\frac{n\lambda }{|B|})w_2-\frac{n}{|B|}\sum _{i\in B}{x}_2^2(x_1^i{w}_1+x_2^i{w}_2+b-y^i)$$
我们可以看到，想对于原来的损失函数，在权重$w$更新的时候，添加了项目$\frac{n\lambda }{|B|}$使得权重更小，是的一些权重无效，来降低拟合度，从而防止过拟合。这也是为什么这种方法被称为权重衰减。

实例

我们以下公式作为对象进行高维线性拟合 。
$$y=0.05+\sum _{i=1}^{p}0.01x+ϵ$$

import torch
import torch.nn as nn
import numpy as np
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l
# 输入维度num_inputs
# 训练集的数量
# 测试集的数量
n_train,n_test,num_inputs=20,100,200
# 初始化w和偏移b
true_w,true_b=torch.ones(num_inputs,1)*0.01,0.05

#看下features的矩阵维度[n_train+n_test,num_inputs]
features=torch.randn((n_train+n_test,num_inputs))
print(features)
#生成标签
labels = torch.matmul(features, true_w) + true_b
print(labels)
print(labels.shape)
#给标签添加绕动项
print(np.random.normal(0,0.01,size=labels.size()).shape)
labels+=torch.tensor(np.random.normal(0,0.01,size=labels.size()),dtype=torch.float)
print(labels.shape)

#生产训练集和测试集
train_features,test_features=features[:n_train,:],features[n_train:,:]
train_labels,test_labels=labels[:n_train],labels[n_train:]
print(train_features.shape)
print(test_features.shape)
print(train_labels.shape)
print(test_labels.shape)

# 对参数进行随机初始化
def init_params():
    w=torch.randn((num_inputs,1),requires_grad=True) #num_input=200
    b=torch.zeros(1,requires_grad=True)
    return [w,b]
 
# 定义L2范数惩罚项
def l2_penalty(w):
    return (w**2).sum()/2

def linreg(X,w,b):
    return torch.mm(X,w)+b

def squared_loss(y_hat,y):
    return (y_hat-y.view(y_hat.size()))**2/2

#定义一个作图函数semilogy,其中y轴使用了对数尺度
def semilogy(x_vals,y_vals,x_label,y_label,x2_vals=None,y2_vals=None,legend=None,figsize=(3.5,2.5)):
    set_figsize(figsize)
    plt.xlabel(x_label)
    plt.ylabel(y_label)
    plt.semilogy(x_vals,y_vals)  #设定y轴为对数尺度 basey：y轴的底需要大于1 semilogx也一样，对应的是x轴的

    if  x2_vals and y2_vals:
        plt.semilogy(x2_vals,y2_vals,linestyle=":")
        plt.legend(legend)    #在图左上角增加背景图例
    plt.show()

#3.2.6定义优化算法
def sgd(params,lr,batch_size):  #本函数已保存在d2lzh_pytorch包中方便以后使用
    for param in params:
        param.data-=lr*param.grad/batch_size  #注意这里更改param时用的param.data

# 定义训练和测试
batch_size,num_epochs,lr=1,100,0.003
net,loss=linreg,squared_loss
print("net=torch.mm(X,w)+b")
print("loss=(y_hat-y.view(y_hat.size()))**2/2")

# 生成数据集与训练集的可迭代对象
dataset=torch.utils.data.TensorDataset(train_features,train_labels)
train_iter=torch.utils.data.DataLoader(dataset,batch_size,shuffle=True)

# 添加训练和测试过程的函数
def fit_and_plot(lambd):
	w,b=init_params()  #初始化权重与偏移量的参数
	train_ls,test_ls=[],[]
	for _ in range(num_epochs):
		for x,y in train_iter:
			# 这里添加L2范数乘法项
			l=loss(net(x,w,b),y)+lambd*l2_penalty(w)  
			#以上l2_penalty的结果是个标量，会广播到每个loss中每个元素，但batch_size等于1，因此[net(x,w,b),y]的结果的shape是[1,1]
			#广播之后只是分配到矩阵的一个元素中，而sum运行之后，也之后一个元素的和，因此结果就不需要除以batch_size了
			#l=l.sum()/batch_size  batch_size=1
			l=l.sum()
			if w.grad is not None:
				w.grad.data.zero_()
				b.grad.data.zero_()
			l.backward()
			sgd([w,b],lr,batch_size)  #手动更新权重与偏移量，grad在w,b里面都会有保存
		train_ls.append(loss(net(train_features,w,b),train_labels).mean().item()) #训练一个epoch之后输出结果
    test_ls.append(loss(net(test_features,w,b),test_labels).mean().item()) #训练一个周期后输出测试结果
	semilogy(range(1,num_epochs+1),train_ls,'epochs','loss',range(1,num_epochs+1),test_ls,['train','test'])
	print('L2 norm of w:',w.norm().item())  #求 L2 范数 ，矩阵内的所有元素加起来后求根号

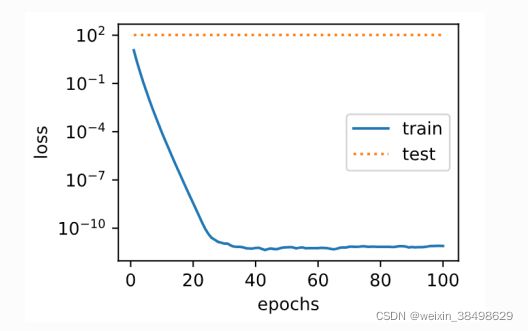
实验结果1

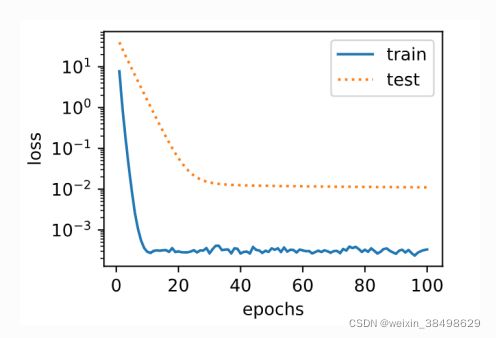
• 现在在预测过程中我们加入权重衰减参数

fit_and_plot(lambd=3)

简洁实现

def fit_and_plot_pytorch(wd):
    # 对权重进行参数衰减。权重名称一般是以weight结尾
    net=nn.Linear(num_inputs,1)
    nn.init.normal_(net.weight,mean=0,std=1)
    nn.init.normal_(net.bias,mean=0,std=1)
    optimizer_w=torch.optim.SGD(params=[net.weight],lr=lr,weight_decay=wd)  #对权重参数衰减
    optimizer_b=torch.optim.SGD(params=[net.bias],lr=lr)  #不对偏移量进行衰减

    train_ls,test_ls=[],[]
    for _ in range(num_epochs):
        for x,y in train_iter:
            l=loss(net(x),y).mean()
            optimizer_w.zero_grad()
            optimizer_b.zero_grad()

            l.backward()

            # 对两个optimizer实例分别调用step函数，从而分别更新权重和偏差量
            optimizer_w.step()
            optimizer_b.step()
        train_ls.append(loss(net(train_features),train_labels).mean().item())
        test_ls.append(loss(net(test_features),test_labels).mean().item())
    d2l.semilogy(range(1,num_epochs+1),train_ls,'epochs','loss',
                        range(1,num_epochs+1),test_ls,['train','test'])
    print('L2 norm of w:',net.weight.data.norm().item())

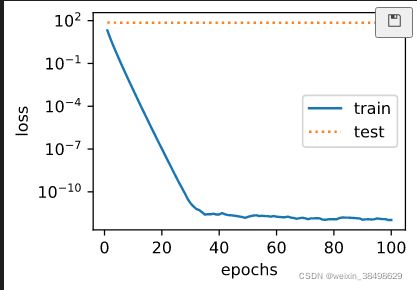
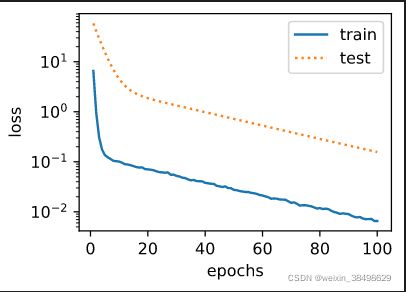
使用权重衰减

fit_and_plot_pytorch(0)

fit_and_plot_pytorch(3)