【图像隐写】FRFT+SVD盲水印嵌入+攻击+提取【含Matlab源码 1757期】
⛄一、基于分数阶傅立叶变换的水印算法简介
1 分数阶傅立叶变换
FRFT可以解释为信号在时频平面内坐标轴绕原点逆时针旋转任意角度后构成的分数阶Fourier域上的表示方法, 它的基本定义是从线性积分变换的角度给出的。定义在t域的函数x (t) 的p阶分数阶傅立叶变换如下:
![]()
式中FRFT的变换核Kp (t, u) 如下:

其中α≡pπ2。记阶数为P的FRFT线性算子为FP。对于二维图像信号x (x, y) , 其二维FRFT如下:
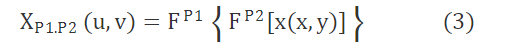
P1和P2表示了在二维空间中的单独分数阶次, 两者可以相同, 也可以不同。当阶数接近于0时, 分数阶傅立叶变换将主要反映信号的时域特征, 当阶数接近于1时, 分数阶傅立叶变换将主要反映信号的频域特征, 为不失一般性, 本文令变换阶数P1=P2=0.3。
2 基于分数阶傅立叶变换的水印算法
2.1 水印的嵌入算法
为了保证水印算法的鲁棒性, 水印应该嵌入到图像的重要分量上, 通常重要分量为变换域系数集中幅值较大的系数。信号的分数阶傅立叶变换系数为一复数, 与变换域水印算法的基本原理相同, 分数阶傅立叶变换域水印的嵌入也是通过对信号的傅立叶变换系数的修改来实现的, 在这里我们采用加性嵌入规则。
(1) 对大小为N×N的图像I(x,y)进行二维分数阶傅立叶变换, 变换阶数为 (0.3, 0.3) , 将二维分数阶傅立叶变换系数按照递减顺序重新排列为序列S={Si|Si≥Si−1}。较大的分数阶傅立叶变换, 系数嵌入水印, 嵌入后的水印图像会产生比较明显的失真;较小的分数阶傅立叶变换系数嵌入水印, 算法对抗压缩和低通滤波攻击的性能不好。所以, 在嵌入水印时将最大的L个系数舍弃不用, 而将水印嵌入其后的M个系数中。
(2) 令水印数据是一个伪随机序列, 序列的长度为M‚R={Ri|i=1,2,…,M}, 那么在这种算法中, 水印的容量就可用伪随机序列的长度M来表示, 便于进行统计分析。
(3) 采用加性规则表示分数阶傅立叶变换域水印嵌入的过程如下:
Swi=Si+αRii=L+1, L+2, …, L+M (4)
其中, α为水印的嵌入强度。
(4) 将嵌入水印之后的序列Swi重新排列为N×N的矩阵, 对其进行变换阶数为 (-0.3, -0.3) 的二维分数阶傅立叶变换, 得到含有水印的图像。
2.2 水印的检测方法
水印的检测过程为水印加入的逆过程, 采用相关检测方法。水印提取的过程如下:将水印图像和原始图像分别进行(0.3,0.3)的分数阶傅立叶变换, 从中抽取值序列V′={v′1,v′2,⋯,vL´}和V={v1,v2,⋯,vL}。利用水印的嵌入公式, 水印的提取如下:
wi = v′i-vi/α (5)
由此得到提取出的水印序列X∗={x1∗,x2∗,⋯,xL∗}, 通过式 (5) 计算X与原来嵌入的水印序列X={x1,x2,⋯,xL}的相似度如下:
![]()
引入一个可以判断X和X是否相似的门限值T, 在实验中, 为减少误判和错判, 一般将T设为6, 如果sim(X,X∗)>6, 就可认为X*是由X派生的。
⛄二、部分源代码
close all;
clear all;
clc;
a=0.5;
alpha=0.08;
A = imread(‘lenaTest3.jpg’);
w = imread(‘cameraman.pgm’);
W=double(w);
[W_IM,S,Uw,Vw ] = embedding(A,W,a,alpha);
[ EX_WM ] = extraction(S,W,W_IM ,a,alpha,Uw,Vw);
[ N_IM ] = addnoise(A,S,W,W_IM ,a,alpha,Uw,Vw);
[ Blur_IM ] = blurring(A,S,W,W_IM ,a,alpha,Uw,Vw);
[ compress_IM ] = compression(A,S,W,W_IM ,a,alpha,Uw,Vw);
[ crop_IM ] = cropping(A,S,W,W_IM ,a,alpha,Uw,Vw );
[R_IM1,R_IM2] = Rotation( A,S,W,W_IM ,a,alpha,Uw,Vw );
[I] = row_col_blank( A,S,W,W_IM ,a,alpha,Uw,Vw );
[ sharp_IM ] = sharpening( A,S,W,W_IM ,a,alpha,Uw,Vw );
[ J] = translation( A, S,W,W_IM ,a,alpha,Uw,Vw);
⛄三、运行结果
⛄四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1]杨守义,姬留杰,穆晓敏,齐林.基于FRFT的数字水印算法分析[J].计算机应用与软件. 2009,26(01)
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除

















