算法笔记十一 —— 图论

图论

1. 图的存储

图的计算机存储方式一般有两种，一种是邻接矩阵的方法，一种是邻接表。

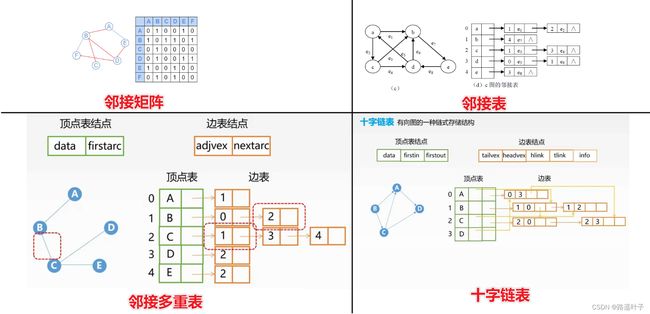
①邻接矩阵

若有$n$个点，则开一个 $n\ast n$的二维数组，其中一维表示起点，另一维则表示终点，其储存的值则可用于表示边的存在与否或者边的权值大小。

int G[maxn][maxn];

//建图
G[start][end]=value;//这里表示的是有向图
//若是无向图则edge[start][end]=edge[end][start]=value
//若无权值，则可用1表示有边，0表示无边

例：邻接矩阵的建立

共 $m+1$ 行，第 1 行为 2 个数，$n$ 和 $m$，分别表示一共有 $n$ 个点（编号为 1 到 $n$）以及$m$ 条有向边。接下来 $m$ 行，每行有两个整数 $X,Y$ 表示边的方向是 X → Y。

输入：
    8 9
	1 3
	7 8
	1 4
	3 7
	2 6
	2 5
	4 7
	4 8
	1 2

#include
#include
#include
using namespace std;

const int maxn = 100;
bool vis[maxn];

//邻接矩阵
int G[maxn][maxn] = { 0 };  //maxn*maxn的二维矩阵

int main()
{
	int n, m;  //点，边
	cin >> n >> m;
	for (int i = 1; i <= m; i++)
	{
		int x, y;
		cin >> x >> y;
		//建图 表示x可以到y ，这里建的是有向图
		G[x-1][y-1] = 1;
		//如果是无向图，可以为：
		//G[x-1][y-1] = G[y-1][x-1] = 1;
	}

	cout << "邻接矩阵：" << endl;
	//展示一下邻接矩阵
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++)
		{
			cout << G[i][j] << " ";
		}
		cout << endl;
	}

	return 0;
}

输出：
	当前邻接矩阵：
	0 1 1 1 0 0 0 0
	0 0 0 0 1 1 0 0
	0 0 0 0 0 0 1 0
	0 0 0 0 0 0 1 1
	0 0 0 0 0 0 0 0
	0 0 0 0 0 0 0 0
	0 0 0 0 0 0 0 1
	0 0 0 0 0 0 0 0

需要注意的是，邻接矩阵的空间复杂度为$O(n^2)$ ，对于点较多的图论题，大概率会超出内存的限制。

②邻接表

刚才已经说到，邻接矩阵在n很大的时候是不行的，所以一般使用邻接表的存储方法。

（1）链表存储

首先是邻接表的正统处理方法，也是效率最高的方法——链表存储。

#include
using namespace std;

const int maxn = 100;


//结点的定义
typedef struct EdgeNode //边表结点
{
	int adjvex; //邻接点域，存储邻接顶点对应的下标
	int weight; //用于存储权值，对于非网图可以不需要
	struct EdgeNode* next; //链域，指向下一个邻接点
}EdgeNode;

typedef struct VertexNode  //顶点表结点
{
	int data;  //顶点域，存储顶点信息
	EdgeNode* firstedge; //边表头指针
}VertexNode, AdjList[maxn];

typedef struct
{
	AdjList adjList;  //顶点表
	int numVertexes, numEdges; //图中当前顶点数和边数
}GraphAdjList;

//建立无向图的邻接表结构
void CreateALGraph(GraphAdjList* G)
{
	int n, m;
	EdgeNode* e;
	cin >> n >> m;
	G->numVertexes = n;
	G->numEdges = m;

	for (int i = 0; i < G->numVertexes; i++)
	{
		G->adjList[i].data = i+1;  //建立顶点表
		G->adjList[i].firstedge = NULL; //将所有边表置为空表
	}

	for (int k = 0; k < G->numEdges; k++)
	{
		int u, v, w;
		cin >> u >> v >> w;
		e = (EdgeNode*)malloc(sizeof(EdgeNode)); //向内存申请空间，生成边表结点
		e->adjvex = v;
		e->weight = w;
		//相当于将e插入到G->adjList[u]这个链表中（头插法)
		e->next = G->adjList[u-1].firstedge;
		G->adjList[u-1].firstedge = e; //将当前顶点的指针指向e

		//无向图，所以还要再反过来重复一次
		e = (EdgeNode*)malloc(sizeof(EdgeNode));
		e->adjvex = u;
		e->weight = w;
		e->next = G->adjList[v-1].firstedge;
		G->adjList[v-1].firstedge = e;
	}

	cout << "当前邻接表：" << endl;
	//展示一下邻接表
	for (int i = 0; i < n; i++) {
		cout << G->adjList[i].data << ":" << endl;
		EdgeNode* tmp = G->adjList[i].firstedge;
		while (tmp != nullptr) {
			cout << G->adjList[i].data << "-" << tmp->adjvex << ":" << tmp->weight << "    ";
			tmp = tmp->next;
		}
		cout << endl;
	}
}

int main() {
	GraphAdjList G;
	CreateALGraph(&G);
	return 0;
}

 输入：
 	8 9
	1 3 1
	7 8 2
	1 4 3
	3 7 4
	2 6 5
	2 5 6
	4 7 7
	4 8 8
	1 2 9
 
 输出：
    当前邻接表：
	1:
	1-2:9    1-4:3    1-3:1
	2:
	2-1:9    2-5:6    2-6:5
	3:
	3-7:4    3-1:1
	4:
	4-8:8    4-7:7    4-1:3
	5:
	5-2:6
	6:
	6-2:5
	7:
	7-4:7    7-3:4    7-8:2
	8:
	8-4:8    8-7:2

（2）用数组存的邻接表

详解看这里：邻接表详解

#include
using namespace std;

const int maxn = 1e5;
const int maxm = 1e5;

struct Edge
{
    int u, v, w;  //一条边的u，v，w
    Edge(int _u = 0, int _v = 0, int _w = 0) { u = _u, v = _v, w = _w; }
    Edge(Edge& e) { u = e.u, v = e.v, w = e.w; }
};

Edge E[maxm + 5];   //存m条边的信息
int head[maxn + 5];   //存n个顶点下第一条边的边序号
int  m_next[maxm + 5];   //存m条边序号之间的关系
int cnt;  //边序号的控制

void init()
{
    cnt = 0;
    memset(head, 0, sizeof(head));
}

void addedge(int u, int v, int w)
{
    E[++cnt] = Edge(u, v, w);  //数组，存边，边的序号取决于到达顺序，此时E[k]表示第k条边(k=1,2,...n)

    //赋值，第k条边到达（该边是u起始的），则应该修改head[u]=k，即该顶点下的第一条边的序号发生修改
    //但是赋值前肯定得看看这个顶点下之前有没有边，如果之前已经有head[u]的值s，表示原来顶点下的第一条边的序号是s
    //那么就在m_next数组中存这个关系，使m_next[k]=s，则表示看完第k条边，下一条边就是s（类似于做了个头插
    m_next[cnt] = head[u];
    head[u] = cnt;
}

int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int u, v, w;
        cin >> u >> v >> w;
        addedge(u, v, w);
    }
    cout << "当前head数组：" << endl;
    for (int i = 1; i <= n; i++) 
        cout << head[i] << "    ";
    cout << endl;


    cout << "当前next数组：" << endl;
    for (int i = 1; i <= m; i++)
        cout << m_next[i] << "    ";
    cout << endl;


    cout << "当前邻接表：" << endl;
    for (int i = 1; i <= n; i++) {
        cout << i << ":" << endl;
        for (int j = head[i]; j; j = m_next[j]) {
            cout << "    " << E[j].u << "-" << E[j].v << ":" << E[j].w;
        }
        cout << endl;
    }
    
}

输入：
	8 9
	1 3 1
	7 8 2
	1 4 3
	3 7 4
	2 6 5
	2 5 6
	4 7 7
	4 8 8
	1 2 9
 
输出：
    当前head数组：
	0    9    6    4    8    0    0    2
	当前next数组：
	0    0    0    1    0    0    5    0    7
	当前邻接表：
	0:
	
	1:
	    1-2:9    1-4:3    1-3:1
	2:
	    2-5:6    2-6:5
	3:
	    3-7:4
	4:
	    4-8:8    4-7:7
	5:
	
	6:
	
	7:
	    7-8:2

（3）vector存储

第三种方法即最简单的STL大法，若有 $n$个点，则开一个大小为$n$ 的vector数组，其中数组下标表示起点，vector中储存的为终点。若需要表示权值，可以使用结构体。

vector<int>edge[maxn];  //注意，这是建立了一个大小为maxn的数组，每个数组的元素是一个vector，相当于是二维数组，第i个元素代表的是一个以i为开头的连续边的集合。

//建图
edge[start].push_back(end);//从start出发，能够到达的点增加了一个end

首先看，没有权值的时候，不需要结构体，建立是最轻松的。

输入：
    8 9
	1 3
	7 8
	1 4
	3 7
	2 6
	2 5
	4 7
	4 8
	1 2

#include
#include
#include
using namespace std;

const int maxn = 100;
bool vis[maxn];

//邻接表
vector<int> a[maxn];  //maxn个存int的vector

int main()
{
	int n, m;  //点，边
	cin >> n >> m;
	for (int i = 1; i <= m; i++)
	{
		int x, y;
		cin >> x >> y;
		//建图 表示x可以到y ，这里建的是有向图
		a[x].push_back(y);
	}

	cout << "当前邻接表：" << endl;
	//展示一下邻接表
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < a[i].size(); j++)
		{
			cout << a[i][j] << " ";
		}
		cout << endl;
	}

	for (int i = 0; i < n; i++)//把每条路所通向的点从小到大排列
		sort(a[i].begin(), a[i].end());//快排  

	cout << "当前邻接表：" << endl;
	//展示一下邻接表
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < a[i].size(); j++)
		{
			cout << a[i][j] << " ";
		}
		cout << endl;
	}

	return 0;
}

输出：
	当前邻接表：
	1:   3 4 2
	2:   6 5
	3:   7
	4:   7 8
	5:
	6:
	7:   8
	8:
	当前邻接表：
	1:   2 3 4
	2:   5 6
	3:   7
	4:   7 8
	5:
	6:
	7:   8
	8:

有权值时，就要上结构体

#include 
#include 
using namespace std;
int const maxn = 1000;  //点
int const maxm = 1000;  //边

struct Edge
{
    int u, v, w;  //一条边的u，v，w
    Edge(int _u = 0, int _v = 0, int _w = 0) { u = _u, v = _v, w = _w; }
};
vector<Edge>G[maxn];  //MAX_N个存边的数组

void addedge(int u, int v, int w)
{
    G[u].push_back(Edge(u, v, w));  //第u个数组是代表第u个点，存的是该点向外的边
}

int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= m; i++)
        G[i].clear();
    for (int i = 1; i <= m; i++) {
        int u, v, w; // u, v, w
        cin >> u >> v >> w;
        addedge(u, v, w);
    }

    cout << "当前邻接表为：" << endl;
    for (int i = 1; i <= n; i++) {
        cout << i << ": ";
        for (int j = 0; j < G[i].size(); j++)   //遍历i连向的所有边
        {
            Edge e = G[i][j];
            cout << e.u << "-" << e.v << ":" << e.w << "    ";
        }
        cout << endl;
    }

}

 输入：
 	8 9
	1 3 1
	7 8 2
	1 4 3
	3 7 4
	2 6 5
	2 5 6
	4 7 7
	4 8 8
	1 2 9


 输出：
    当前邻接表为：
	1: 1-3:1    1-4:3    1-2:9
	2: 2-6:5    2-5:6
	3: 3-7:4
	4: 4-7:7    4-8:8
	5:
	6:
	7: 7-8:2
	8:

④链式向前星

如果说邻接表是不好写但效率好，邻接矩阵是好写但效率低的话，前向星就是一个相对中庸的数据结构。前向星固然好写，但效率并不高。而在优化为链式前向星后，效率也得到了较大的提升。虽然说，世界上对链式前向星的使用并不是很广泛，但在不愿意写复杂的邻接表的情况下，链式前向星也是一个很优秀的数据结构。 ——摘自《百度百科》

链式前向星其实就是静态建立的邻接表，时间效率为O（m），空间效率也为O（m）。遍历效率也为O（m）。

#include 
#include 
using namespace std;

/*
int const MAX_N = 1000;  //点
int const MAX_M = 1000;  //边

struct Edge
{
    int to, cost, next;
};
vectorG[MAX_N];  //MAX_N个存边的数组

void addedge(int u, int v, int c)
{
    Edge newEdge;
    newEdge.to = u;
    newEdge.next = v;
    newEdge.cost = c;
    G[u].push_back(newEdge);  //第u个数组是代表第u个点，存的是该点向外的边
}
*/

using namespace std;
const int maxn = 1005;//点数最大值
int n, m, cnt;//n个点，m条边
struct Edge
{
    int to, w, next;//终点，边权，同起点的上一条边的编号
}edge[maxn];//边集

int head[maxn];//head[i],表示以i为起点的第一条边在边集数组的位置（编号）

void init()//初始化
{
    for (int i = 0; i <= n; i++) head[i] = -1;
    cnt = 0;
}
void add_edge(int u, int v, int w)//加边，u起点，v终点，w边权
{
    edge[cnt].to = v; //终点
    edge[cnt].w = w; //权值
    edge[cnt].next = head[u];//以u为起点上一条边的编号，也就是与这个边起点相同的上一条边的编号
    head[u] = cnt++;//更新以u为起点上一条边的编号
}
int main()
{
    cin >> n >> m;
    int u, v, w;
    init();//初始化
    for (int i = 1; i <= m; i++)//输入m条边
    {
        cin >> u >> v >> w;
        add_edge(u, v, w);//加边
        /*
        加双向边
        add_edge(u, v, w);
        add_edge(v, u, w);
        */
    }
    for (int i = 1; i <= n; i++)//n个起点
    {
        cout << i << ":" << endl;
        for (int j = head[i]; j != -1; j = edge[j].next)//遍历以i为起点的边
        {
            cout << i << "-" << edge[j].to << ":" << edge[j].w << endl;
        }
        cout << endl;
    }
    return 0;
}

 输出：
	1:
	1-2:9
	1-4:3
	1-3:1
	
	2:
	2-5:6
	2-6:5
	
	3:
	3-7:4
	
	4:
	4-8:8
	4-7:7
	
	5:
	
	6:
	
	7:
	7-8:2
	
	8:

2. 图的遍历

①DFS（深度优先搜索）

DFS的特点是，顺着当前的路径一直往后遍历，直到无点可访问时，再返回上一级节点。

以上图为例——假设对所有可访问的节点，将优先访问编号小的节点。

则我们从0号节点出发，前往当前可访问的最小编号节点2。

过程为0-2-3。此时到3已无可访问节点，于是放回上一级。

总过程为0-2-3-4-1-5。

void dfs(int now)
{
	vis[now] = 1;
	cout << now << " ";
	for (int i = 0; i < a[now].size(); i++)//遍历当前点可到达的所有节点
	{
		int next = a[now][i];
		if (!vis[next]) {
			dfs(next);
		}//如果尚未访问，则递归下去访问
	}
}

②BFS（广度优先搜索）

BFS的特点是，将当前所在节点可访问的所有节点都加入队列，等全都访问过后再前往下一层。

还是以上图为例，BFS的过程将是0-2-4-5-3-1。

void bfs(int start)
{
	queue<int>q;//访问队列
	q.push(start);
	cout << start << " ";
	vis[start] = 1;
	while (!q.empty())
	{
		int now = q.front();
		for (int i = 0; i < a[now].size(); i++)
		{
			int next = a[now][i];
			if (!vis[next]) {
				q.push(next);
				vis[next] = 1;
				cout << next << " ";
			}
		}
		q.pop();
	}
}

1. 【深基18.例3】查找文献

p5318

题目描述

小K 喜欢翻看洛谷博客获取知识。每篇文章可能会有若干个（也有可能没有）参考文献的链接指向别的博客文章。小K 求知欲旺盛，如果他看了某篇文章，那么他一定会去看这篇文章的参考文献（如果他之前已经看过这篇参考文献的话就不用再看它了）。

假设洛谷博客里面一共有 $n(n\le 10^5)$ 篇文章（编号为 1 到 $n$）以及 $m(m\le 10^6)$ 条参考文献引用关系。目前小 K 已经打开了编号为 1 的一篇文章，请帮助小 K 设计一种方法，使小 K 可以不重复、不遗漏的看完所有他能看到的文章。

这边是已经整理好的参考文献关系图，其中，文献 X → Y 表示文章 X 有参考文献 Y。不保证编号为 1 的文章没有被其他文章引用。

请对这个图分别进行 DFS 和 BFS，并输出遍历结果。如果有很多篇文章可以参阅，请先看编号较小的那篇(因此你可能需要先排序)。

输入格式

共 $m+1$ 行，第 1 行为 2 个数，$n$ 和 $m$，分别表示一共有 $n(n\le 10^5)$ 篇文章（编号为 1 到 $n$）以及$m(m\le 10^6)$ 条参考文献引用关系。

接下来 $m$ 行，每行有两个整数 $X,Y$ 表示文章 X 有参考文献 Y。

输出格式

共 2 行。
第一行为 DFS 遍历结果，第二行为 BFS 遍历结果。

样例输入 #1

8 9
1 2
1 3
1 4
2 5
2 6
3 7
4 7
4 8
7 8

样例输出 #1

1 2 5 6 3 7 8 4 
1 2 3 4 5 6 7 8

题解——BFS和DFS的应用

#include
#include
#include
#include
#include
using namespace std;

const int maxn = 100005;
bool vis[maxn];
vector<int> a[maxn];  //maxn个存int的vector

void dfs(int now)
{
	vis[now] = 1;
	cout << now << " ";
	for (int i = 0; i < a[now].size(); i++)//遍历当前点可到达的所有节点
	{
		int next = a[now][i];
		if (!vis[next]) {
			dfs(next);
		}//如果尚未访问，则递归下去访问
	}
}
void bfs(int start)
{
	queue<int>q;//访问队列
	q.push(start);
	cout << start << " ";
	vis[start] = 1;
	while (!q.empty())
	{
		int now = q.front();
		for (int i = 0; i < a[now].size(); i++)
		{
			int next = a[now][i];
			if (!vis[next]) {
				q.push(next);
				vis[next] = 1;
				cout << next << " ";
			}
		}
		q.pop();
	}
}

int main()
{
	int n, m;
	cin >> n >> m;
	for (int i = 1; i <= m; i++)
	{
		int x, y;
		cin >> x >> y;
		a[x].push_back(y);//建图 表示x可以到y 
	}

	/*cout << "当前邻接表：" << endl;
	//展示一下邻接表
	for (int i = 1; i <= n; i++) {
		for (int j = 0; j < a[i].size(); j++)
		{
			cout << a[i][j] << " ";
		}
		cout << endl;
	}*/


	for (int i = 1; i <= n; i++) {
		//把每条路所通向的点从小到大排列（题目中有要求） 
		sort(a[i].begin(), a[i].end());
	} 

	/*	cout << "当前邻接表：" << endl;
	//展示一下邻接表
	for (int i = 1; i <= n; i++) {
		for (int j = 0; j < a[i].size(); j++)
		{
			cout << a[i][j] << " ";
		}
		cout << endl;
	}*/

	for (int i = 1; i <= n; i++)
		vis[i] = false;
	dfs(1);//进行深搜

	cout << endl;

	for (int i = 1; i <= n; i++) 
		vis[i] = false;
	bfs(1);//进行广搜 

	return 0;
}

2. 图的遍历

p3916

题目描述
给出 $N$ 个点，$M$ 条边的有向图，对于每个点 $v$，求 $A(v)$ 表示从点 $v$ 出发，能到达的编号最大的点。

输入格式

第 $1$ 行 $2$ 个整数 $N,M$，表示点数和边数。

接下来 $M$ 行，每行 $2$ 个整数 $U_i,V_i$，表示边 $(U_i,V_i)$。点用 $1,2,\dots ,N$ 编号。

输出格式

一行 $N$ 个整数 $A(1),A(2),\dots ,A(N)$。

样例输入 #1

4 3
1 2
2 4
4 3

样例输出 #1

4 4 3 4

提示

• 对于 $60\%$ 的数据，$1\le N,M\le 10^3$。
• 对于 $100\%$ 的数据，$1\le N,M\le 10^5$。

题解——DFS的应用及优化

下面的代码，直接走DFS的思想，每次都为start找到最大能到达的点返回，这样时间复杂度太高了，简单的能够处理，但是数据量大时就TLE了

#include
#include
#include
using namespace std;

const int maxn = 100005;
bool vis[maxn];
vector<int> a[maxn];  //maxn个存int的vector

int getmax(int now, int max_now)
{
	vis[now] = 1;
	for (int i = 0; i < a[now].size(); i++)  //遍历当前点可到达的所有节点
	{
		if (a[now][i] > max_now)
			max_now = a[now][i];  //最后一个节点，是当前层级可到达的最大的节点
		int next = a[now][i];
		if (!vis[next]) 
			max_now = getmax(next, max_now);  //递归下去访问
	}
	return max_now;
}


int main()
{
	int n, m;
	cin >> n >> m;
	for (int i = 1; i <= m; i++)
	{
		int x, y;
		cin >> x >> y;
		a[x].push_back(y);//建图 表示x可以到y 
	}

	for (int i = 1; i <= n; i++) {
		//把每条路所通向的点从小到大排列 
		sort(a[i].begin(), a[i].end());
	} 
	
	for (int i = 1; i <= n; i++) {
		for (int i = 1; i <= n; i++)
			vis[i] = false;
		cout << getmax(i, i) << " ";
	}
	
	return 0;
}

AC：①反向建图；②用DFS的思想，但是是从最大的点开始，反向找能到达的点

#include
#include
#include
#include
#include
using namespace std;

const int maxn = 100005;
bool vis[maxn];
vector<int> a[maxn];  //maxn个存int的vector
int max_d[maxn];

void dfs_max(int now, int start) {
	vis[now] = 1;
	if (max_d[now])
		return;
	max_d[now] = start;  //如果start能到达点now，那么点now能达到最大的点就是start，下次再递归到now点时，不用再递归
	for (int i = 0; i < a[now].size(); i++)//遍历当前点可到达的所有节点
	{
		int next = a[now][i];
		if (!vis[next]) {
			dfs_max(next, start);
		}
	}
}

int main()
{
	int n, m;
	cin >> n >> m;
	for (int i = 1; i <= m; i++)
	{
		int x, y;
		cin >> x >> y;
		a[y].push_back(x);  //反着建图
	}

	for (int i = n; i >= 1; i--) {
		dfs_max(i, i);
	}

	for (int i = 1; i <= n; i++)
	{
		cout << max_d[i] << " ";
	}

	return 0;
}