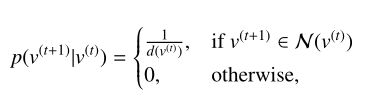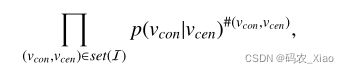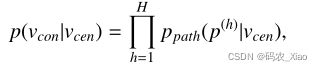图嵌入综述

目录

一、图嵌入是什么

二、图嵌入要解决的两个关键性问题

1.要保存哪些信息？

2.如何保存这些信息？

三、图嵌入的总体流程框架

四、简单图的图嵌入

1）保持节点共现(deepwalk)

1.Mapping Function映射函数

2.基于随机游走的共现抽取器(Extractor)

3.重构器（Reconsructor）和目标(Objective)

4实现难点：

---

目录

一、图嵌入是什么

二、图嵌入要解决的两个关键性问题

1.要保存哪些信息？

2.如何保存这些信息？

三、图嵌入的总体流程框架

四、简单图的图嵌入

1）保持节点共现(deepwalk)

1.Mapping Function映射函数

2.基于随机游走的共现抽取器(Extractor)

3.重构器（Reconsructor）和目标(Objective)

4.实现难点

5.分层softmax

6.负采样

---

一、图嵌入是什么

图嵌入的目的是将给定图中的每个节点映射为低维向量表示（或通常称为节点嵌入），该表示通常保留原始图中节点的一些关键信息。图中的节点可以从两个域查看：

1）原始图域，其中节点通过边（或图结构）连接；

2）嵌入域，其中每个节点表示为连续向量。

二、图嵌入要解决的两个关键性问题

1.要保存哪些信息？

如节点的邻域信息、节点的结构角色、节点状态和社区信息等。

2.如何保存这些信息？

保存信息的方法的技术细节各不相同，但大多数方法都有相同的思想，即使用嵌入域中的节点表示来重构要保留的图域信息。直觉是那些好的节点表示应该能够重建我们想要保存的信息。因此，可以通过最小化重建误差来学习映射。

三、图嵌入的总体流程框架

•  Mapping: 将节点从图域映射到嵌入域的映射函数。
• Extracrot: 从图域提取预保留信息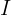的信息提取器。
• Reconstructor: 通过嵌入域的embeddings重新构造提取的信息 。
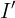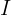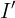• Objective: 一个基于信息和重构信息的目标，通常通过优化这个目标来学习映射函数或者重构器中的参数。

四、简单图的图嵌入

1）保持节点共现(deepwalk)

1.Mapping Function映射函数

定义映射函数的直接方法是使用查找表。这意味着我们根据节点的索引i检索其嵌入。

                                                                                   （1）

其中是N（N是所有节点热编码的个数）维空间各个方向的分量都是0或1的向量，除此之外必有一个元素=1,其他元素全为0。

其中是要学习的嵌入参数，d表示嵌入的维数。W中的第i行就是节点的表示（embedding），映射函数中的参数为N和d。

2.基于随机游走的共现抽取器(Extractor)

随机游走的定义：

给定一个图,从初始点开始随机跳T个邻居节点，称为长度为T的随机游走。

选择下一跳节点的概率如下：

 其中表示节点的度，表示节点的邻域集。

换句话说就是按照均匀分布从领域中选取下一跳节点。

为了生成能够捕获整个图信息的随机游动，将每个节点视为生成γ个随机游走的起始节点。因此，总共存在N*个γ随机游走。该过程如算法1所示。该算法的输入包括图G、随机游动的长度T和每个起始节点的随机游动数γ。从算法1的第4行到第8行，我们为V中的每个节点生成γ随机游走，并将这些随机游走添加到R中。最后，R是算法的输出，由N*γ生成的随机游动组成。

                                        那么如何从随机游走中提取出共现关系呢？

以顶点集V中所有节点为初始点，进行T跳的随机游走，每一个T跳的随机游走看作一个句子。

对于一个句子中给定的中心词，距离这个中心词一定跳数的词称为上下文，那么中心词和上下文是共现的。用一个元组（vcon,vcen）表示共现关系，其中vcon表示上下文中的一点，vcen表示中心节点。

 从伪代码可以看出。遍历所有随机游走生成的”句子“集合，迭代的对属于这个顶点的随机游走生成它的共现表。

共现表的生成过程为：从j=1到跳数T循环增加元组和元组进入节点的共现列表。循环往复可得到所有节点的共现表。

3.重构器（Reconsructor）和目标(Objective)

                                       如何利用嵌入域的表示重构共现信息？

每个节点有两重身份（中心节点/上下文），使用两个映射函数为每个节点生成对应身份得节点表示。

中心节点映射函数：                              （2）

上下文节点映射函数：                           （3）

对于一个元组（vcon,vcen）,共现关系就是在中心节点vcen得上下文中观察到vcon，可以通过以上两个映射函数，用SoftMax函数建模：

                                                    （4）

 表示对于任意元组（vcon,vcen）重构器可以返回的期望。

重构器的目标是从嵌入域中准确的提取原始图的信息（如共现关系，节点状态等），那么就要求重构器从信息(共现表)中提取元组（vcon,vecn）的概率很高，而随机生成元组的概率很低。

因为中的重复的元组肯定很多，因此对重构信息的概率可以建模为

                                                （5）

set(I)是不存在重复的元组集合，#(vcon, vcen)是元组(vcon, vcen)在中的频率。因此元组出现的越频繁重构器的效果越好，要是（5）最大化，则需要学习的参数和的建模为：

               （6）

4.实现难点

在实际的编程中实现（4）的计算是不可行的，因此通常采用分层的softmax或者负采样。

5.分层softmax

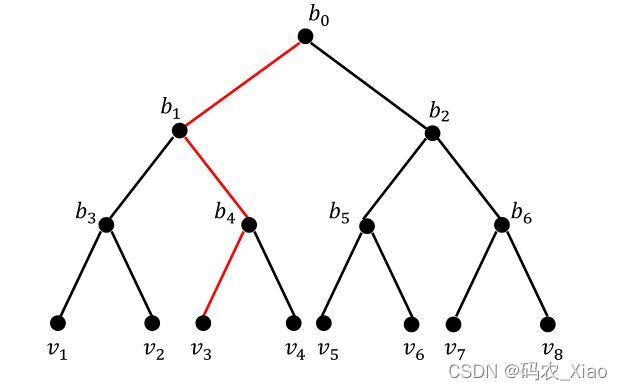
在分层的softmax中途中的所有节点会分配到一个二叉树上。例如：

               

定义从根节点到v3的路径(b0，b1，b4,v3)为(,,,)其中对应根节点b0,对应上下文节点vcon=v3.

那么在以中心节点v8的环境下观察到上下文节点v3的概率表示为

                                                                  （7）

由此可以推出

 =**

                      =**

除此之外定义 

                                                                         （8） 

表示b1由节点b0从左边走到

并且定义的计算表达式为：

                                                                         （9）

                              （10）

 其中为一个对二叉树中节点的映射函数，为对图G中节点的映射函数。

为一个sigmoid函数，将概率归一化。

通过以上式子就将从学习对图G中的中心节点和上下文节点的映射函数转换为学习一个对二叉树内部节点的映射函数和一个对图G节点的映射函数。

6.负采样