卡尔曼滤波估计小车匀加速运动

本文主要内容借鉴http://blog.csdn.net/heyijia0327/article/details/17487467博客当中的内容。

有一个匀加速运动的小车，它受到的合力为 ft , 由匀加速运动的位移和速度公式，能得到由 t-1 到 t 时刻的位移和速度变化公式：

                                                 

该系统系统的状态向量包括位移和速度，分别用 xt 和 xt的导数 表示。控制输入变量为u，也就是加速度，于是有如下形式:

                                           

所以这个系统的状态的方程为：

                                         

这里对应的的矩阵A大小为 2*2 ,矩阵B大小为 2*1。 

      貌似有了这个模型就能完全估计系统状态了，速度能计算出，位移也能计算出。那还要卡尔曼干嘛，问题是很多实际系统复杂到根本就建不了模。并且，即使你建立了较为准确的模型，只要你在某一步有误差，由递推公式，很可能不断将你的误差放大A倍（A就是那个状态转换矩阵），以至于最后得到的估计结果完全不能用了。回到最开始的那个笑话，如果那个完全凭预测的特种兵在某一步偏离了正确的路径，当他站在错误的路径上（而他自己以为是正确的）做下一步预测时，肯定走的路径也会错了，到最后越走越偏。

     既然如此，我们就引进反馈。从概率论贝叶斯模型的观点来看前面预测的结果就是先验，测量出的结果就是后验。

     测量值当然是由系统状态变量映射出来的，方程形式如下：

                                        

注意Z是测量值，大小为m*1(不是n*1，也不是1*1，后面将说明），H也是状态变量到测量的转换矩阵。大小为m*n。随机变量v是测量噪声。

     同时对于匀加速模型，假设下车是匀加速远离我们，我们站在原点用超声波仪器测量小车离我们的距离。

                                            

也就是测量值直接等于位移。可能又会问，为什么不直接用测量值呢？测量值噪声太大了，根本不能直接用它来进行计算。试想一个本来是朝着一个方向做匀加速运动的小车，你测出来的位移确是前后移动（噪声影响），只根据测量的结果，你就以为车子一会往前开一会往后开。

对于状态方程中的系统噪声w和测量噪声v，假设服从如下多元高斯分布，并且w,v是相互独立的。其中Q,R为噪声变量的协方差矩阵。

                               

看到这里自然要提个问题，为什么噪声模型就得服从高斯分布呢？请继续往下看。

      对于小车匀加速运动的的模型，假设系统的噪声向量只存在速度分量上，且速度噪声的方差是一个常量0.01，位移分量上的系统噪声为0。测量值只有位移，它的协方差矩阵大小是1*1，就是测量噪声的方差本身。

那么：

                                         

Q中，叠加在速度上系统噪声方差为0.01，位移上的为0，它们间协方差为0，即噪声间没有关联。

使用卡尔曼滤波器估计小车匀加速运动的

matlab程序如下：

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 %日 期： 	2015.10.12
 %程序功能：	使用卡尔曼滤波器估计小车匀加速运动
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 
clear all  
  
% 初始化参数  
delta_t=0.1;   %采样时间  
t=0:delta_t:5;  
N = length(t); % 序列的长度  
sz = [2,N];    % 信号需开辟的内存空间大小  2行*N列  2:为状态向量的维数n  
g=10;          %加速度值 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 
x=1/2*g*t.^2;      %实际真实位置  
z = x + sqrt(10).*randn(1,N); % 测量时加入测量白噪声  
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%  
Q =[0 0;0 9e-1]; %假设建立的模型  噪声方差叠加在速度上 大小为n*n方阵 n=状态向量的维数  
R = 10;    % 位置测量方差估计，可以改变它来看不同效果  m*m      m=z(i)的维数  
  
A=[1 delta_t;0 1];  % n*n  
B=[1/2*delta_t^2;delta_t];  
H=[1,0];            % m*n  
  
n=size(Q);  %n为一个1*2的向量  Q为方阵  
m=size(R);  
  
% 分配空间  
xhat=zeros(sz);       % x的后验估计  
P=zeros(n);           % 后验方差估计  n*n  
xhatminus=zeros(sz);  % x的先验估计  
Pminus=zeros(n);      % n*n  
K=zeros(n(1),m(1));   % Kalman增益  n*m  
I=eye(n);  
  
% 估计的初始值都为默认的0，即P=[0 0;0 0],xhat=0  
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%EKF过程
for k = 9:N           %假设车子已经运动9个delta_T了，我们才开始估计  
    % 时间更新过程  
    xhatminus(:,k) = A*xhat(:,k-1)+B*g;  
    Pminus= A*P*A'+Q;  
      
    % 测量更新过程  
    K = Pminus*H'*inv( H*Pminus*H'+R );  
    xhat(:,k) = xhatminus(:,k)+K*(z(k)-H*xhatminus(:,k));  
    P = (I-K*H)*Pminus;  
end  
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%   
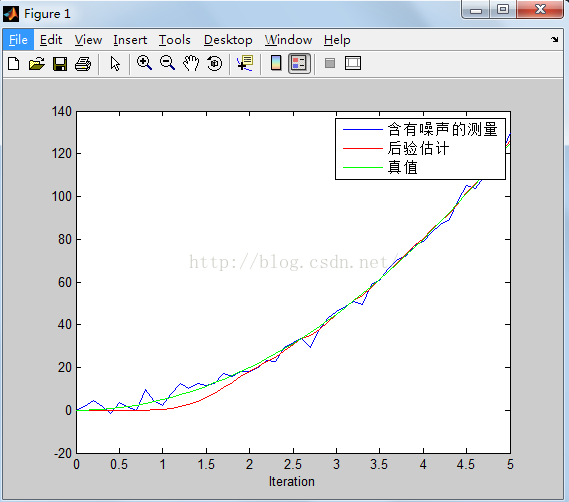
figure(1)  
plot(t,z);  
hold on  
plot(t,xhat(1,:),'r-')  
plot(t,x(1,:),'g-');  
legend('含有噪声的测量', '后验估计', '真值');  
xlabel('Iteration'); 

%% Estimate error(估计误差)
x_error = x-xhat(1,:);

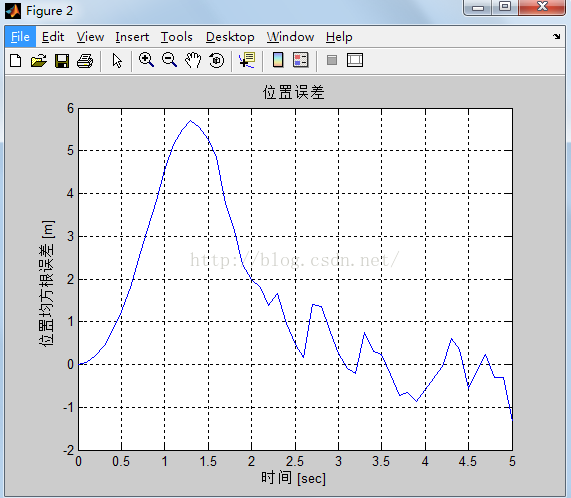
%% Graph 2
figure(2) 
plot(t,x_error(1,:)),grid on;
title('位置误差')
xlabel('时间 [sec]')
ylabel('位置均方根误差 [m]')
hold off;

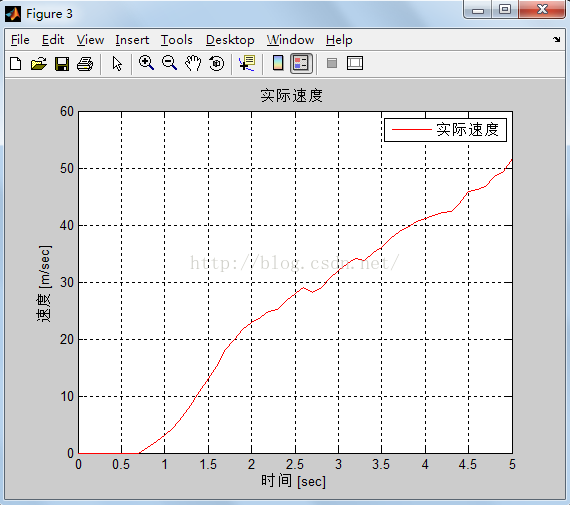
%% Graph 3
figure(3)
plot(t,xhat(2,:),'r'),grid on;
title('实际速度 ')
legend('实际速度')
xlabel('时间 [sec]')
ylabel('速度 [m/sec]')
hold off;
%==========================================================================

运行结果如下：