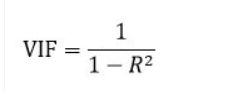R语言第七讲 线性回归分析案例续

 

题目
          MASS 库中包含 Boston (波士顿房价)数据集，它记录了波士顿周围 506 个街区的 medv (房价中位数)。我们将设法用 13 个预测变量如 rm (每栋住宅的平均房间数)， age (平均房 龄)， lstat (社会经济地位低的家庭所占比例)等来预测 medv (房价中位数)。

************************************************MASS是R语言自带的库********************************************************

       上一篇文章介绍了简单线性回归的分析案例，接下来介绍一下多元线性回归的分析案例。数据集，还是继续使用上一节的Boston数据集，读者自行加载数据集，在此不做赘述。

       为了用最小二乘法拟合多元线性回归模型，再次调用 lm ()函数。语句 lm (y ~ x1 + x2 + x3) 用于建立有三个预测变量 xl ， x2 和 x3 的拟合模型。 summary ( )函数输出所有预测变 量的回归系数。

> lm.fit=lm(medv~lstat+age,data=Boston)
> summary(lm.fit)
Call:
lm(formula = medv ~ lstat + age, data = Boston)

Residuals:  
    Min      1Q  Median      3Q     Max 
-15.981  -3.978  -1.283   1.968  23.158 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 33.22276    0.73085  45.458  < 2e-16 ***
lstat       -1.03207    0.04819 -21.416  < 2e-16 ***
age          0.03454    0.01223   2.826  0.00491 ** 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 6.173 on 503 degrees of freedom
Multiple R-squared:  0.5513,	Adjusted R-squared:  0.5495 
F-statistic:   309 on 2 and 503 DF,  p-value: < 2.2e-16

       从以上数据看以看到函数的残差(中等残差只有-1.283，函数拟合模型相对较好，#估计标准误差t值，#预测的残差标准误，R方，F统计量和p值。F统计量309的值，相当大了，表示medv与Istat和age确实有线性关系。自由度503，表示有503个点不受限制。

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 33.22276    0.73085  45.458  < 2e-16 ***
lstat       -1.03207    0.04819 -21.416  < 2e-16 ***
age          0.03454    0.01223   2.826  0.00491 ** 

       以上数据分析，截距和Istat系数、age系数的值分别为33.22276   ，-1.03207， 0.03454 ，系数的标准差均小于1，说明估计出的系数较为稳定，而且p值均小于0.05，说明有较大的证据证明medv与Istat和age有线性关系。

      Boston 数据集包含 13 个变量，所以在用所有的预测变量进行回归时，一一输入会很麻 烦。可以使用下面的快捷方法:

> lm.fit = lm(medv~.,data = Boston)
> summary(lm.fit)

Call:
lm(formula = medv ~ ., data = Boston)

Residuals:
    Min      1Q  Median      3Q     Max 
-15.595  -2.730  -0.518   1.777  26.199 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  3.646e+01  5.103e+00   7.144 3.28e-12 ***
crim        -1.080e-01  3.286e-02  -3.287 0.001087 ** 
zn           4.642e-02  1.373e-02   3.382 0.000778 ***
indus        2.056e-02  6.150e-02   0.334 0.738288    
chas         2.687e+00  8.616e-01   3.118 0.001925 ** 
nox         -1.777e+01  3.820e+00  -4.651 4.25e-06 ***
rm           3.810e+00  4.179e-01   9.116  < 2e-16 ***
age          6.922e-04  1.321e-02   0.052 0.958229    
dis         -1.476e+00  1.995e-01  -7.398 6.01e-13 ***
rad          3.060e-01  6.635e-02   4.613 5.07e-06 ***
tax         -1.233e-02  3.760e-03  -3.280 0.001112 ** 
ptratio     -9.527e-01  1.308e-01  -7.283 1.31e-12 ***
black        9.312e-03  2.686e-03   3.467 0.000573 ***
lstat       -5.248e-01  5.072e-02 -10.347  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.745 on 492 degrees of freedom
Multiple R-squared:  0.7406,	Adjusted R-squared:  0.7338 
F-statistic: 108.1 on 13 and 492 DF,  p-value: < 2.2e-16

      可以用它们的名字访问 summary的各个组成部分(输入? summary.lm 查看可用项)。因此, summary (lm. f i t ) $ r. sq 可输出可以输出R方， summary(lm.fit) $sigma可给出RSE， vif ()函数是 car 包的一部分，可用于计算方差膨胀因子。此数据集中大多数变量的 VIF 值是低到中等。 Car 包不是 R 基本配置的一部分，因此第一次时使用必须通过install.packages 命令下载。

> install.packages("car")
> library(car)
> vif(lm.fit)#计算方差膨胀因子
    crim       zn    indus     chas      nox       rm      age      dis 
1.792192 2.298758 3.991596 1.073995 4.393720 1.933744 3.100826 3.955945 
     rad      tax  ptratio    black    lstat 
7.484496 9.008554 1.799084 1.348521 2.941491 

 方差膨胀因子  

       假设有n个非零向量X1,X2, …,Xn，如果存在不全等于零的常数b1, b2, …, bn使得b1X1+b2X2+b3X3+…+bnXn=0，则认为X1,X2,…,Xn之间存在线性关系。多重共线性也是相似的道理。在实际建模的过程中，我们的数据集常常含有成千上万个样本，其中某几个变量之间存在非常严格的线性关系的情况是几乎不可能存在的，因此当解释变量之间存在一定程度的相关性（近似共线性）时，也可以称之为多重共线性。当有多重共线性的情况发生时，参数估计的结果不再具有有效性，因此在进行逻辑回归分析之前我们需要通过VIF检验来排除掉某些有多重共线性的变量。
    VIF指的是解释变量之间存在多重共线性时的方差与不存在多重共线性时的方差之比，可以反映多重共线性导致的方差的增加程度。它的公式长这样：

    

       如果想用除某一变量之外的所有其他变量进行回归，该如何操作?例如，在上面的回归结 果中， age 变量有很高的 p 值。所以我们不妨进行不包括年龄变量的回归。下面的语句就是用 除 age 之外的所有预测变量进行回归。或者使用 update ()函数。

> lm.fit1=lm(medv~.-age,data=Boston)
> summary(lm.fit1)
> lm.fit1=update(lm.fit, ~.-age)

Call:
lm(formula = medv ~ . - age, data = Boston)

Residuals:
     Min       1Q   Median       3Q      Max 
-15.6054  -2.7313  -0.5188   1.7601  26.2243 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  36.436927   5.080119   7.172 2.72e-12 ***
crim         -0.108006   0.032832  -3.290 0.001075 ** 
zn            0.046334   0.013613   3.404 0.000719 ***
indus         0.020562   0.061433   0.335 0.737989    
chas          2.689026   0.859598   3.128 0.001863 ** 
nox         -17.713540   3.679308  -4.814 1.97e-06 ***
rm            3.814394   0.408480   9.338  < 2e-16 ***
dis          -1.478612   0.190611  -7.757 5.03e-14 ***
rad           0.305786   0.066089   4.627 4.75e-06 ***
tax          -0.012329   0.003755  -3.283 0.001099 ** 
ptratio      -0.952211   0.130294  -7.308 1.10e-12 ***
black         0.009321   0.002678   3.481 0.000544 ***
lstat        -0.523852   0.047625 -10.999  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.74 on 493 degrees of freedom
Multiple R-squared:  0.7406,	Adjusted R-squared:  0.7343 
F-statistic: 117.3 on 12 and 493 DF,  p-value: < 2.2e-16