【论文阅读】Graph Fusion Network for Text Classification

基于图融合网络的文本分类

原论文链接地址：https://www.sciencedirect.com/science/article/abs/pii/S0950705121009217
论文作者：Yong Dai, Linjun Shou, Ming Gong, Xiaolin Xia, Zhao Kang, Zenglin Xu, Daxin Jiang

GFN

GNN方法存在两个主要局限性：（1）这些方法无法轻松适应新文档；（2） 其中大多数忽略了文本图的质量。这些阻碍了其在实际场景中的广泛应用。GFN由图构造阶段和图推理阶段组成。在图构建阶段，GFN设法克服了上述两个限制。具体来说，对于第一个限制，GFN没有将所有文档预先定义为文本图中的节点，而是放弃文档级节点，构建纯单词级文本图。为了生成文档嵌入，GFN根据文档级别的结构信息实时融合单词嵌入。这样，当面对新文档时，系统不需要重建文本图和重新训练学习系统。对于第二个限制，众所周知，构建一个能够准确捕获所有结构知识的理想文本图是一项重要的任务，而用不同的方法构建文本图可能包含不同的信息视图。因此，GFN通过将外部知识（即预先计算的共现统计和预先训练的嵌入）转换为结构信息来构建不同的语料库级别的图，并将它们集成以相互补偿。
在图推理过程中，GFN采用三个步骤（即图学习、图卷积和图融合）来提高系统性能。首先，GFN添加了一个图学习步骤来调整初始化的边权重，以更好地服务于任务。然后，GFN采用消息传递机制进行图卷积计算。最后，GFN应用了一种晚期融合范式（即融合逻辑或最终决策结果），它由一个精心设计的基于多头的融合模块组成，以在图融合步骤中整合来自每个图的结果。重要的是，与早期融合范式（即特征级融合）不同，晚期融合带来了许多优势。首先，它避免了由于噪声和每个图中包含的无关信息而造成的早期交叉污染。其次，它继承了集成学习的鲁棒性和良好的经验性能。第三，晚期融合范式保留了多样性表征能力。GFN的算法流程图如图1所示。

图1 算法流程图。首先为每个文档$d_k$构建文本图{$G_{s,d_k}(V_{d_k}，E_{s,d_k})$}${}_{s=1}^4$，然后调整文档级文本图以更好地服务于分类任务，实现图卷积，最后整合所有逻辑以获得更好的决策边界。

1.文本图的构造

(1)符号标记

文本图表示为{$G_s=(V，E_s)$}${}_{s=1}^{n_G}$，其中V（|V|=n）和E_s是相应文本图的节点集和边集。s∈ [1，n_G]是文本图索引，n_G=4，这意味着在该文中构建了四种语料库级文本图。V由语料库中的所有单词组成。e_s,ij（E_s的元素）表示单词w_i和w_j之间的关系，这是通过指标计算的。此外，将节点特征矩阵表示为$X\in R^{n\times d}$和节点特征向量$x_i\in R^d$（即嵌入单词w_i），其中d是特征维度。存在邻接矩阵$A_s\in R^{n\times n}$对应于每个E_s，其中包括所有字对字关系。E_s可以视为A_s的子集，在某些条件下会被过滤和保留。例如，如果元素a_s,ij在A_s中的值（按某个度量计算）等于零，这意味着单词i和单词j之间的关系很弱，不会包含在E_s中。系统的学习过程为：

1. 更新每个边集E_s，其中的元素由公式初始化和计算；
2. 更新节点特征矩阵X；
3. 更新其他网络参数。

实际上，为每个文档$d_k$构建子图{$G_{s,d_k}=（V_{d_k}，E_{s,d_k}）$}${}_{s=1}^4$，并逐步迭代地更新系统，其中$V_{d_k}$中的节点是文档中的单词，边集$E_{s,d_k}$是$E_s$的子集。

(2)图构造

基于以下知识和四个不同的度量构造每个文本图$G_s(V，E_s)$

1. 基于共现统计的图构造
共现统计使从业者能够在较高的水平上理解给定文本文档中所说的内容，这已通过许多预训练模型进行了验证，例如word2vec、GloVe等。单词-单词共现矩阵的每个条目都是以单词w_i的出现为条件，单词对（w_i，w_j）出现概率的最大似然估计值（MLE），其公式如下：
$$P_{ML}(w_i|w_j)=\frac{\#(w_i,w_j)}{\#(w_i)}$$
它表示两个单词（w₁、w₂）的全局关系。在这个公式中，$\#(w_i)$是单词w_i的出现次数，$\#(w_i,w_j)$是两个单词在预定义和固定大小的窗口L中一起出现的次数。如前所述，单词共现分析发现单词对之间的意思相似，因此我们让$e_{ij}=P_{ML}（w_j|w_i）$，其中值越大，关系越密切。

2. 基于正逐点互信息的图构造
逐点互信息（PMI）被广泛用于单词相似性任务。通过考虑语料库中的实际观察次数，可以根据经验对其进行估计：
$$PMI(w_i,w_j)=log\frac{\#(w_i,w_j)\cdot |D|}{\#(w_i)\cdot \#(w_j)}$$
其中D是单词对的集合，|D|是单词对计数。$PMI(w_i,w_j)$通过计算它们的联合概率及其边际概率之比的对数来衡量单词对$(w_i,w_j)$之间的关系。负PMI通常意味着单词之间的弱关联，因此采用了正PMI（PPMI）度量：
$$PPMI(w_i,w_j)=max(PMI(w_i,w_j),0)$$
PPMI度量可以被视为共现度量的重加权变体。在某些场景中，PPMI表现得更好，比如语义相似性任务。因此，可以设置$e_{ij}=PPMI（w_i,w_j）$。

3. 基于预处理嵌入余弦相似性的图构造
良好的表达可以捕获隐藏在文本数据中的隐含语言规则和常识知识，例如词汇意义、句法结构、语义角色，甚至语用。因此，衡量单词之间关系的另一个合理方法是利用预先训练的单词嵌入。为了从单词嵌入中提取知识并测量单词对之间的关系，本文选择余弦相似性和欧氏距离作为两种度量，因为余弦相似性和欧氏距离已经被广泛用于测量句子对关系和单词对关系。欧氏距离更关注大小差异，而余弦相似性更关注方向（角度）。具体来说，单词对的余弦相似性由以下公式表示：
$$cos(x_i,x_j)=\frac{x_i\cdot x_j}{|x_i|\cdot |x_j|}$$
其中，x_i和x_j分别是单词w_i和w_j的嵌入。值越大，两个单词之间的距离越近。

4. 基于预处理嵌入欧氏距离的图构造
单词对的欧氏距离公式为：$euc(x_i,x_j)=||x_i-x_j|{|}_2$

5.为每个文档构建子图
基于这四个度量构建四种语料库级文本图。为了避免来自不相关关系的噪声，本文排除了由四个度量计算的负值或较小值的关系。考虑到内存消耗，本文在小批量文档上训练GFN，而不是每一步都训练整个文档。为每个文档$d_k$构建子图{$G_{s,d_k}=（V_{d_k}，E_{s,d_k}）$}${}_{s=1}^4$。节点集$V_{d_k}$由$d_k$中的m个单词组成，k是文档索引。边集$E_{s,d_k}$是从$E_s$获取的。此外，当$w_j$位于$w_i$的词尾时，我们将$w_i$和$w_j$之间的一条边添加到$G_{s,d_k}$中，因为这类信息有利于中心词$w_i$的表示。总体而言，文档级子图包括两种关系：语料库级关系和邻域关系。

2.图推理

本节展示了GFN的推理过程。GFN通过以下三个步骤对文档级子图进行推理：图学习、图卷积和图融合。

(1)图学习

假设预先计算的$E_s$可能不是最优的，需要根据下游任务进行调整。对于$w_i$和$w_j$之间的边$e_{s,ij}$，学习过程可以表述为：${\tilde{e}}_{s,ij}=ReLU(a_{s,ij}\cdot e_{s,ij})$，其中ReLU(·)=max(0，·)，$a_{s,ij}$是一个可学习参数。ReLU保证了${\tilde{e}}_{s,ij}$的非负性。通过公式，可以导出文档$d_k$的自适应文本子图${\tilde{G}}_{s,d_k}(V_{d_k},{\tilde{E}}_{s,d_k})$。

(2)图卷积

在图学习之后，采用消息传递机制来聚合来自邻居的信息，并通过吸收聚合的信息来更新节点特征。如果消息传递阶段为T个时间步长，则中间时间步长的聚合函数可以表示为：
$$m_{s,i}^{t+1}=\frac{1}{|Nei(w_i)|}\sum _{j=1}^{|Nei(w_i)|}({\tilde{e}}_{s,ij}\cdot h_{s,j}^{t+1})$$
其中$|Nei(w_i)|$是$w_i$的邻居数，$h_{s,j}^{t+1}\in R^{1\times d_h}$是$w_i$邻居的中间隐藏状态，j是$w_i$邻域词的索引和$d_h$是隐藏状态的维度。
每个节点$w_i$的隐藏状态$h_{s,i}^{t+1}\in R^{1\times d_h}$通过吸收邻域消息来更新，根据公式：$$h_{s,i}^{t+1}=h_{s,i}^t+m_{s,i}^{t+1}$$
$h_{s,i}^{t+1}$（$w_i$的隐藏状态）由上次的隐藏状态及其邻居的消息组成。在单词级特征更新后，我们可以通过以下方式获得每个文档的表示和最后logits（即Softmax之前的非正规概率）：
$$d_{s,k}=\frac{1}{|d_k|}\sum _{i=1}^{|d_k|}(h_{s,i}^T|\forall w_i\in d_k),$$
$$logit{s}_{s,k}=ReLU(d_{s,k})W_s$$
其中$d_{s,k}\in R^{1\times d_h}$，$W_s\in R^{d_h\times c}$，$logit{s}_{s,k}\in R^{1\times c}$，c表示类别数。$d_{s,k}$（文档的嵌入）是通过平均文档$d_k$中所有单词的最后隐藏状态得到的。将$d_{s,k}$投影到标签空间，以获得最终的logits $logit{s}_{s,k}$。

(3)图融合

下标s（s∈ [1，4]）表示每个文档有4种视图。为了集成不同的视图并搜索一致的决策边界，该论文设计了一个融合模块。具体来说，首先连接$logit{s}_{s,k}$：
$$logit{s}_k=|{|}_{s=1}^{4}logit{s}_{s,k}$$
其中，||是连接运算符和$logit{s}_k\in R^{1\times c\times 4}$。受其他论文的启发，该论文开发了一种多头部变体作为融合算子，以充分利用模型的容量，其公式如下：
$$hea{d}_i={\Gamma }_{{\phi }_i}(logit{s}_k)$$
其中${\Gamma }_{{\phi }_i}$是由${\phi }_i$参数化的融合算子，$hea{d}_i\in R^{1\times c}$是第i个$(i\in [1，|h|])$融合意见的头。融合算子${\Gamma }_{{\phi }_i}$的目的是将4种不同的意见融合为一致的意见，这是整个系统性能的关键。实际上，本文使用核大小为$[4，|h|，1]$的卷积层来聚合不同的观点。卷积的行为就像一个加权池，将多视图意见简化为单个决策。
然后，|h|决策头部被平均化，以生成文档$d_k$的最终决策：
$$\widehat{logit{s}_k}=\frac{1}{|h|}\sum _{i=1}^{|h|}hea{d}_i$$
$$\widehat{y_k}=Softmax(\widehat{logit{s}_k})$$
其中，|h|是头数，$\widehat{logit{s}_k}\in R^{1\times c}和\widehat{y_k}\in R^{1\times c}$。融合过程如图2所示。

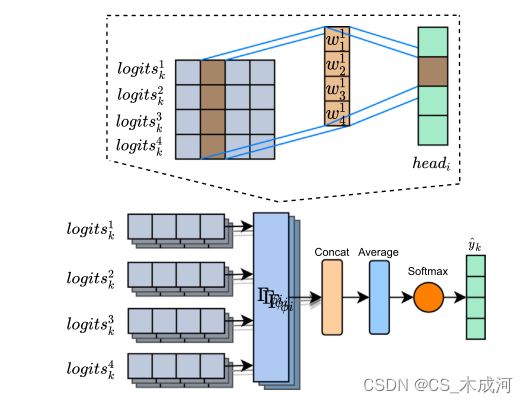
图2 图融合过程。每个头接受四个logit，代表属于每个类别的非正规概率的不同view，并输出综合决策。多个头获得不同的决策，这些决策将通过softmax函数进一步平均和规范化。

最后，最小化了模型优化中基本真值标签$y_k$和预测标签${\hat{y}}_k$之间的交叉熵损失：
$$L=-\sum _k{y}_{k}log{\hat{y}}_k$$

实验结果

GFN在五个基准数据集上使用两组基线的性能。表2给出了精度测试结果。总体而言，GFN的性能始终优于其他基线。具体来说，GFN在20NG、Oh和MR上分别获得0.8701、0.7020和0.7804，这与之前的工作相比是明显的提升。
R8和R52的改进并不明显，作者认为这是因为：
（1）这些数据集的任务比其他数据集的简单，所以它们对复杂的功能编码器没有强烈的要求。
（2） 这两个数据集的精度太高，无法提高。

Micro-F1和Macro-F1的结果如表3所示，从中可以观察到与基线相比有明显的提高。

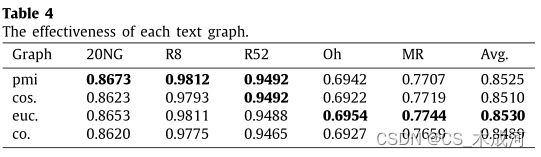
探讨每个文本图的有效性。为此轮流将GFN与每个单个文本图（即PMI、余弦相似性、欧氏距离和共现）相适应，并在没有融合模块的情况下测试系统性能。通过采用不同的图（表示为“mi”、“cos.”、”uc.“和”co.“），给出了系统性能，如表4所示。
可以得出结论，每个文本图捕获的结构信息都是不同的，这导致了不同的性能。PMI诱导文本图和欧氏距离诱导文本图支持的GFN表现良好，而具有共现诱导图的GFN则表现较差。

评估有多少头足够系统。作者用GFN做了不同头部的实验。结果如表5所示，从中可以看出，GFN采用三个头时表现最好。

结论

在该论文中，作者提出了一种图融合网络（GFN），它支持对新文档的有效推理，而无需对系统进行再训练，并且可以通过整合文本图的不同视图更好地捕获结构信息。实验结果表明了该方法的优越性。特别是，不同的图视图是互补的，精心设计的多头部融合模块可以进一步提高系统性能。GFN将两种知识转换为结构化信息，以捕获信息的不同方面，但构建理想文本图的问题也未得到解决。可以继续探索其他方法来构建包含更多信息的文本图或自动构建文本图。另一方面，预先训练的模型（如BERT）由于其出色的性能，已经主导了包括文本分类在内的许多领域，而基于GNN的模型也有其优势。因此，对BERT风格模型和基于GNN的模型进行全面的比较分析是有价值的。

原论文链接地址：https://www.sciencedirect.com/science/article/abs/pii/S0950705121009217