Matlab-矩阵

目录

（一）矩阵的操作

1、创建矩阵

​（1）建立简单矩阵

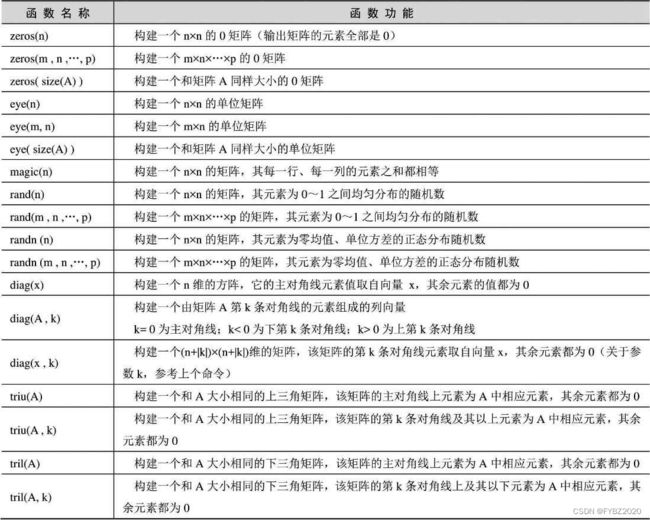
（2）建立特殊矩阵

（3）希尔伯特（Hilbert）矩阵

（4）托普利兹（Toeplitz）矩阵

（5）0～1间均匀分布的随机矩阵

 （6）标准正态分布随机矩阵

（7）魔方矩阵

（8）帕斯卡矩阵

（9）范德蒙（Vandermonde）矩阵

2、矩阵下标的引用

3、改变矩阵的大小和结构

（1）矩阵的合并

（2）矩阵行列的删除

 

---

（一）矩阵的操作

1、创建矩阵

对矩阵的基本操作，主要有矩阵的构造、矩阵大小及结构的改变、矩阵下标引用、矩阵信息的获取等。对于这些操作，MATLAB中都有固定指令或相应的库函数与之相对应。

矩阵和数组在MATLAB中存在很多方面的区别，主要有以下几个方面：
●　矩阵是数学上的概念，而数组是计算机程序设计领域的概念。
●　作为一种变换或者映射运算符的体现，矩阵运算有着明确而严格的数学规则；而数组运算是MATLAB软件定义的规则，其目的是使数据管理方便，操作简单，命令形式自然，执行计算有效。
        两者间的联系主要体现在：在MATLAB中，矩阵是以数组的形式存在的。因此，一维数组相当于向量，二维数组相当于矩阵，所以矩阵是数组的子集。

矩阵的构造方式有两种，一种与单元数组相似，可以对变量直接进行赋值；

另一种是使用MATLAB中提供的构造特殊矩阵的函数，

 （1）建立简单矩阵

简单矩阵采用矩阵构造符号——方括号“[]”，将矩阵元素置于方括号内，同行元素之间用空格或逗号隔开，行与行之间用分号“;”隔开，格式如下：

分别构造一个二维矩阵、一个行向量、一个列向量

（2）建立特殊矩阵

特殊矩阵是指非零元素或零元素的分布有一定规律的矩阵，常见的特殊矩阵有对称矩阵、三角矩阵和对角矩阵等。 

向量、标量和空矩阵
通常情况下，矩阵包含m行n列，即m×n。当m和n取一些特殊值时，得到的矩阵具有一些特殊的性质。
当m=1或n=1，即1×n或m×1时，建立的矩阵称为向量。例如输入： 当m=n=1时，建立的矩阵称为标量。任意以1×1的矩阵形式表示的单个实数、复数都是标量。 单个实数或复数在MATLAB中都是以矩阵的形式存储的；在MATLAB中，单个数据或由单个数据构造的矩阵都是标量。 

当m=n=0，或者m=0，或者n=0，即0×0、0×n、m×0时，创建的矩阵称为空矩阵。空矩阵可以通过赋值语句建立。例如输入：

空矩阵和0矩阵的本质区别在于：空矩阵内没有任何元素，因此不占用任何存储空间；而0矩阵表示该矩阵中的所有元素全部为0，需要占用一定的存储空间。  

MATLAB中生成特殊矩阵的指令集 

（3）希尔伯特（Hilbert）矩阵

希尔伯特矩阵，也称H阵，其元素为Hij=1/(i+j-1)。由于它是一个条件数差的矩阵，所以将它用来作为试验矩阵。
关于希尔伯特矩阵的指令函数如下。
●　hilb(n)：用于生成一个n×n的希尔伯特矩阵。
●　invhilb(n)：用于生成一个n×n的希尔伯特矩阵的逆矩阵整数矩阵。
希尔伯特矩阵生成示例：希尔伯特矩阵和它的逆矩阵都是对称矩阵。 

（4）托普利兹（Toeplitz）矩阵

托普利兹矩阵，它由两个向量定义，即一个行向量和一个列向量。对称的托普利兹矩阵由单一向量来定义。
关于托普利兹矩阵的指令函数如下。
●　toeplitz(k,r)：用于生成非对称托普利兹矩阵，第1列为k，第1行为r，其余元素等于其左上角元素。
●　toeplitz(c)：用于用向量c生成一个对称的托普利兹矩阵。
托普利兹矩阵函数示例：

（5）0～1间均匀分布的随机矩阵

在MATLAB中常用rand()函数产生0～1间均匀分布的随机矩阵，其调用格式如下。
●　r=rand(n)：产生维数为n×n的0～1间均匀分布的随机矩阵。
●　r=rand(m,n)：产生维数为n×m的0～1间均匀分布的随机矩阵。
●　r=rand(m,n,p,...)：产生维数为n×m×p的0～1间均匀分布的随机矩阵。
●　r=rand(size(A))：产生维数为n×m×p与矩阵A相同的0～1间均匀分布的随机矩阵。
创建0～1间均匀分布的随机矩阵示例：

 （6）标准正态分布随机矩阵

在MATLAB中常用randn()函数产生均值为0、方差为1的随机矩阵，其调用格式如下。
●　r=randn(n)。
●　r=randn(m,n)。
●　r=randn(m,n,p,...)。
●　r=randn([m,n,p,...])。
●　r=randn(size(A))。
其格式可参考上述rand()函数。
创建标准正态分布随机矩阵示例

（7）魔方矩阵

在MATLAB中常用magic()函数产生魔方矩阵。

魔方矩阵中每行、每列和两条对角线上的元素和相等，其调用格式如下。

● M=magic(n)。

创建魔方矩阵示例：

（8）帕斯卡矩阵

在MATLAB中常用pascal()函数产生帕斯卡矩阵，其调用格式如下。
●　A=pascal(n)：返回n阶的对称正定Pascal矩阵，其中的元素是由Pascal三角组成的，其逆矩阵的元素都是整数。

 ●    A=pascal(n,1)：返回由下三角的Cholesky因子组成的Pascal矩阵，它是对称的，所以它是自己的逆。
●　A=pascal(n,2)：返回pascal(n,1)的转置和交换形式。A是单位矩阵的立方根。
创建帕斯卡矩阵示例：

（9）范德蒙（Vandermonde）矩阵

在MATLAB中常用vander()函数产生范德蒙矩阵，其调用格式如下。
●　A=vander(v)：生成范德蒙矩阵，矩阵的列是向量v的幂，即A(i,j)=v(i)^(n-j)，其中n=length(v)。
生成范德蒙矩阵示例： 

使用vander()函数产生范德蒙矩阵，输入向量可以是行向量或列向量。

2、矩阵下标的引用

在MATLAB中，普通二维数组元素的数字索引分为双下标索引和单下标索引。

双下标索引是通过一个二元数组对来对应元素在矩阵中的行列位置，例如A(2,3)表示矩阵A中第2行第3列的元素。

单下标索引的方式是采用列元素优先的原则，对m行n列的矩阵按列排序进行重组，成为一维数组，再取新的一维数组中的元素位置对应的值作为元素在原矩阵中的单下标。例如对于4×4的矩阵，A(7)表示矩阵A中第3行第2列的元素，而A(13)表示矩阵A中第1行第4列的元素。

 矩阵中某一元素的单下标索引值和双下标索引值之间，可以通过MATLAB内部函数进行转换，其句法形式为：

其功能为将双下标索引值转换为单下标索引值，其中siz是一个包含两个元素的数组，代表了转换矩阵的行列数，一般可以直接用size(A)表示；i与j分别是双下标索引中的行、列值；IND是转换后的单下标索引值。 

访问多个矩阵元素
设A=magic(4)，如果需要计算第4列元素的和，按照前面介绍的方法则可以用以下表达式来实现：
A(1,4)+A(2,4)+A(3,4)+A(4,4)
在下标表达式中，可以用冒号来表示矩阵的多个元素。例如，A(1:k,j)表示矩阵第j列的前k个元素。利用冒号，计算第4列元素的和可以用更为简洁的式子，代码设置如下：

因为冒号本身可以表示一列或一行的所有元素，所以上式还可以写为： 

在MATLAB中提供了一个关键字end，用于表示该维中的最后一个元素，所以上式还可以改写成：  

3、改变矩阵的大小和结构

根据运算时的不同情况和需要，矩阵大小及结构的改变方式主要有旋转矩阵、改变矩阵维度、删除矩阵元素等。

（1）矩阵的合并

 

矩阵的合并就是把两个或者两个以上的矩阵数据连接起来得到一个新的矩阵。

针对二维矩阵A、B：
（1）[A,B]表示按列存储合并矩阵，即将B矩阵接到A矩阵的列后面；

          [A;B]表示按行存储合并矩阵，即将B矩阵接到A矩阵的行后面。
（2）cat(1,A,B)表示[A;B]，即以行存储；cat(2,A,B)表示[A,B]；
          cat(3,A,B)表示以第3维组合A、B，组合后变成三维矩阵。

前面介绍的矩阵构造符[]不仅可用于构造矩阵，同时还可以作为一个矩阵合并操作符。

表达式C=[A B]在水平方向上合并矩阵A和B，而表达式C=[A;B]在竖直方向上合并矩阵A和B。

可以用矩阵合并符来构造任意大小的矩阵。不过需要注意的是，在矩阵合并的过程中一定要保持矩阵的形状是方形，否则矩阵合并将无法进行。

图1表明具有相同高度的两个矩阵可以在水平方向上合并为一个新的矩阵。而图2则表明不具有相同高度的两个矩阵不允许合并为一个矩阵。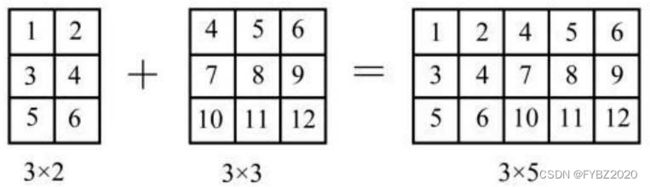

 

（2）矩阵行列的删除

要删除矩阵的某一行或某一列，只要将该行或该列赋予一个空矩阵“[]”即可。

如果想删除矩阵A的第2行，则可以使用如下语句：

 矩阵重构的两个比较重要的运算是转置和共轭转置，在MATLAB中，用在函数后面加撇号“'”来表示。在线性代数的专业书籍中，这种运算经常用*和H表示。

如果A是一个实数矩阵，那么它被转置时，第1行变成第1列，第2行变成第2列……以此类推，一个m×n矩阵变为一个n×m矩阵。如果矩阵是方阵，那么这个矩阵在主对角线上反映出来。如果矩阵A的元素aij是复数，那么所有元素也是共轭的。

如果仅希望转置，则在撇号“'”之前输入一个点号，即成为“.'”，A.'表示转置，其结果与conj(A')相同。如果A是实数矩阵，那么A'与A.'相同。