k近邻回归算法python_K-近邻回归算法的实用介绍（附Python代码）

介绍

在我所遇到的所有机器学习算法中，KNN很容易被选择。尽管它很简单，但它在某些任务上被证明是非常有效的(如本文中所见)。

甚至更好？它可以用于分类和回归问题！然而，它更广泛地用于分类问题。我很少看到KNN在任何回归任务上被实现。我的目的是说明和强调KNN在目标变量本质上是连续的时，如何同样有效。

在本文中，我们将首先理解KNN算法背后的直觉，看看计算点之间距离的不同方法，然后最后在大马特销售数据集上的Python中实现该算法。行动起来吧！

目录表

1.理解KNN背后直觉的一个简单例子

2.KNN算法是如何工作的？

3.点间距离的计算方法

4.如何选择K因子？

5.在数据集上工作

6.追加资源

一 理解KNN背后直觉的一个简单例子

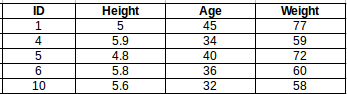
让我们从一个简单的例子开始。考虑下表，它包括10人的身高、年龄和体重(目标)值。如您所见，ID11的权重值丢失。我们需要根据身高和年龄来预测这个人的体重。

注意：本表中的数据不代表实际值。它只是作为一个例子来解释这个概念。

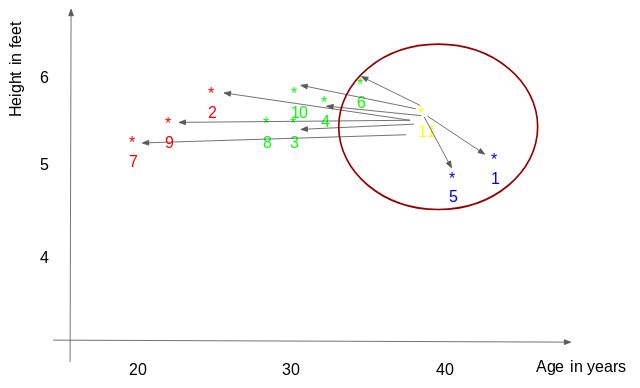
为了更清楚地理解这一点，下面是上面表格中的身高与年龄的曲线图：

在上面的图中，Y轴代表一个人的身高(英尺)，X轴代表年龄(年)。根据ID值对这些点进行编号。黄色点(ID 11)是我们的测试点。

如果我要求你根据情节找出ID11的权重，你会怎么回答？您可能会说，因为ID11更接近点5和1，所以它必须具有与这些ID类似的权重，可能介于72-77kg之间(表中ID1和ID5的权重)。这是有道理的，但是你认为算法是如何预测这些值的呢？我们将在本文中找到这一点。

二 KNN算法是如何工作的？

正如我们上面看到的，KNN可以用于分类和回归问题。该算法使用“特征相似度”来预测任何新的数据点的值。这意味着新的点被指派了一个基于它与训练集中的点有多么密切的值。从我们的例子中，我们知道ID11的高度和年龄与ID1和ID5相似，所以权重也大致相同。

如果它是一个分类问题，我们就把这个模式作为最终的预测。在这种情况下，我们有两个权重值72和77。有人猜测最终值是如何计算的吗？取平均值作为最终预测值。

下面是对算法的逐步解释：

1.首先，计算新点与每个训练点之间的距离。

2.选择最接近的k个数据点(基于距离)。在这个例子中，如果k的值为3，将选择点1, 5, 6。本文将进一步探讨K选择正确值的方法。

3.这些数据点的平均值是对新点的最终预测。在这里，我们的重量ID11 =(77 + 72 + 60)/ 3＝69.66公斤。

在接下来的几节中，我们将详细讨论这三个步骤中的每一个。

三 点间距离的计算方法

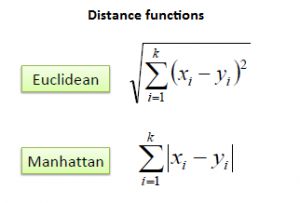
第一步是计算新点和每个训练点之间的距离。有多种计算这种距离的方法，其中最常见的方法是欧几里得法、曼哈顿法(用于连续)和汉明法(用于分类)。

—欧几里得距离：欧几里得距离被计算为新点(x)和现有点(y)之间的平方差之和的平方根。

—曼哈顿距离：这是使用绝对差之和的实向量之间的距离。

—Hamming距离：它用于分类变量。如果预测值(x)和实际值(y)相同，则距离d等于0。否则D＝1。

一旦从训练集中的点测量到一个新的观察点的距离，下一步就是选择最接近的点。要考虑的点数是由K的值定义的。

四 如何选择K因子？

第二步是选择K值。这决定了当我们给任何新的观测值赋值时，我们所看到的邻居的数量。

在我们的例子中，对于一个值k＝3，最近的点是ID1、ID5和ID6。

ID11的权重预测将是：

ID 11＝(77＋72＋60)／3

ID 11＝69.66kg

对于k＝5的值，最接近的点将是ID1、ID4、ID5、ID6、ID10。

ID11的预测将是：

ID 11＝(77＋59＋72＋60＋58)/5



ID 11＝65.2kg

我们注意到，基于K值，最终结果趋于改变。那么我们如何计算K的最佳值呢？让我们根据列车和验证集的错误计算来决定它(毕竟，最小化错误是我们的最终目标！).

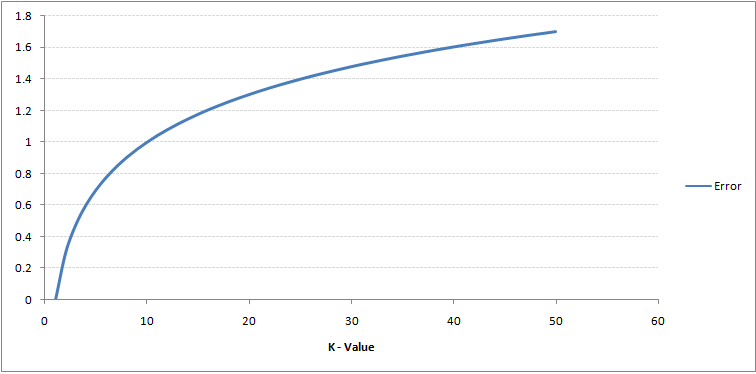
请看下面的图，对于不同k值的训练误差和验证误差。

对于非常低的k值(假设k=1)，该模型在训练数据上重合，这导致验证集上的高错误率。另一方面，对于高k值，该模型在训练和验证集上都表现不佳。如果仔细观察，验证误差曲线在k＝9的值处达到最小值。K的这个值是模型的最佳值(对于不同的数据集，它会变化)。这种曲线被称为“肘部曲线”(因为它有一个形状像肘部)，通常用于确定K值。

您也可以使用网格搜索技术来找到最好的K值。我们将在下一节中实现这一点。

五 数据集的工作(Python代码)

现在你必须对算法有一个清晰的理解。如果你有任何相同的问题，请使用下面的评论部分，我很乐意回答他们。现在我们将继续在数据集上实现算法。我已经使用了大超市销售数据集来显示实现，你可以从这个链接下载它。

1.读取文件

import pandas as pd

df = pd.read_csv('train.csv')

df.head()

2.归入缺失值

df.isnull().sum()

#missing values in Item_weight and Outlet_size needs to be imputed

mean = df['Item_Weight'].mean() #imputing item_weight with mean

df['Item_Weight'].fillna(mean, inplace =True)

mode = df['Outlet_Size'].mode() #imputing outlet size with mode

df['Outlet_Size'].fillna(mode[0], inplace =True)

3.处理分类变量并删除ID列

df.drop(['Item_Identifier', 'Outlet_Identifier'], axis=1, inplace=True)

df = pd.get_dummies(df)

4.创建训练和测试集

from sklearn.model_selection import train_test_split

train , test = train_test_split(df, test_size = 0.3)

x_train = train.drop('Item_Outlet_Sales', axis=1)

y_train = train['Item_Outlet_Sales']

x_test = test.drop('Item_Outlet_Sales', axis = 1)

y_test = test['Item_Outlet_Sales']

5.预处理-缩放特征

from sklearn.preprocessing import MinMaxScaler

scaler = MinMaxScaler(feature_range=(0, 1))

x_train_scaled = scaler.fit_transform(x_train)

x_train = pd.DataFrame(x_train_scaled)

x_test_scaled = scaler.fit_transform(x_test)

x_test = pd.DataFrame(x_test_scaled)

6。让我们看看不同k值的错误率。

#import required packages

from sklearn import neighbors

from sklearn.metrics import mean_squared_error

from math import sqrt

import matplotlib.pyplot as plt

%matplotlib inline

rmse_val = [] #to store rmse values for different k

for K in range(20):

K = K+1

model = neighbors.KNeighborsRegressor(n_neighbors = K)

model.fit(x_train, y_train) #fit the model

pred=model.predict(x_test) #make prediction on test seterror = sqrt(mean_squared_error(y_test,pred)) #calculate rmse

rmse_val.append(error) #store rmse values

print('RMSE value for k= ' , K , 'is:', error)

输出：

RMSE value for k = 1 is: 1579.8352322344945

RMSE value for k = 2 is: 1362.7748806138618

RMSE value for k = 3 is: 1278.868577489459

RMSE value for k = 4 is: 1249.338516122638

RMSE value for k = 5 is: 1235.4514224035129

RMSE value for k = 6 is: 1233.2711649472913

RMSE value for k = 7 is: 1219.0633086651026

RMSE value for k = 8 is: 1222.244674933665

RMSE value for k = 9 is: 1219.5895059285074

RMSE value for k = 10 is: 1225.106137547365

RMSE value for k = 11 is: 1229.540283771085

RMSE value for k = 12 is: 1239.1504407152086

RMSE value for k = 13 is: 1242.3726040709887

RMSE value for k = 14 is: 1251.505810196545

RMSE value for k = 15 is: 1253.190119191363

RMSE value for k = 16 is: 1258.802262564038

RMSE value for k = 17 is: 1260.884931441893

RMSE value for k = 18 is: 1265.5133661294733

RMSE value for k = 19 is: 1269.619416217394

RMSE value for k = 20 is: 1272.10881411344

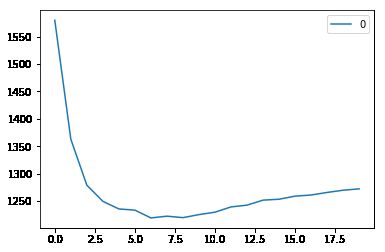
#plotting the rmse values against k values

curve = pd.DataFrame(rmse_val) #elbow curve

curve.plot()

如我们所讨论的，当我们取k＝1时，我们得到一个非常高的RMSE值。当我们增加K值时，RMSE值减小。在K＝7时，RMSE约为1219.06，并进一步增加K值。我们可以肯定地说，k＝7将在这种情况下给我们最好的结果。

这些是使用我们的训练数据集的预测。现在让我们预测测试数据集的值并提交。

7.测试数据集的预测

#reading test and submission files

test = pd.read_csv('test.csv')

submission = pd.read_csv('SampleSubmission.csv')

submission['Item_Identifier'] = test['Item_Identifier']

submission['Outlet_Identifier'] = test['Outlet_Identifier']

#preprocessing test dataset

test.drop(['Item_Identifier', 'Outlet_Identifier'], axis=1, inplace=True)

test['Item_Weight'].fillna(mean, inplace =True)

test = pd.get_dummies(test)

test_scaled = scaler.fit_transform(test)

test = pd.DataFrame(test_scaled)

#predicting on the test set and creating submission file

predict = model.predict(test)

submission['Item_Outlet_Sales'] = predict

submission.to_csv('submit_file.csv',index=False)

在提交这个文件时，我得到了1279.5159651297的RMSE。

8.实现网格搜索引擎

为确定K值，每次绘制弯头曲线是一个繁琐而繁琐的过程。您可以简单地使用GrdSead找到最佳值。

from sklearn.model_selection import GridSearchCV

params = {'n_neighbors':[2,3,4,5,6,7,8,9]}

knn = neighbors.KNeighborsRegressor()

model = GridSearchCV(knn, params, cv=5)

model.fit(x_train,y_train)

model.best_params_

输出：

{'n_neighbors': 7}

六 期末笔记和附加资源

在本文中，我们介绍了KNN算法的工作原理及其在Python中的实现。它是最基本、最有效的机器学习技术之一。对于R语言中的KNN实现，您可以使用R-KNN算法进行本文。

在本文中，我们直接从SKLearn库使用KNN模型。你也可以从头开始实现KNN(我推荐这个！)这是本文所涉及的：KNN简化。

原作者：Aishwarya Singh，热衷于探索无尽的数据科学和人工智能世界的读者。被ML和AI无限的应用所吸引，渴望学习和发现数据科学的深度。