【电力系统】基于粒子群优化潮流计算附matlab代码

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

个人主页：Matlab科研工作室

个人信条：格物致知。

更多Matlab仿真内容点击

智能优化算法  神经网络预测 雷达通信  无线传感器

信号处理 图像处理 路径规划 元胞自动机 无人机  电力系统

⛄ 内容介绍

Optimal Power flow(OPF) is allocating loads to plants for minimum cost while meeting the network constraints. It is formulated as an optimization problem of minimizing the total fuel cost of all committed plant while meeting the network(power flow ) constraints. The variants of the problems are numerous which model the objective and the constraints in different ways.

The basic OPF problem can described mathematically as a minimization of problem of Minimizing the total fuel cost of all committed plants subject to the constraints.

⛄ 部分代码

function [Pgg P V Ybus]=pflow(busdata,linedata);

 % formation of  Y bus

j=sqrt(-1); 

nl = linedata(:,1); nr = linedata(:,2); R = linedata(:,3);

X = linedata(:,4); Bc = j*linedata(:,5); a = linedata(:, 6);

nbr=length(linedata(:,1)); nbus = max(max(nl), max(nr));

Z = R + j*X; y= ones(nbr,1)./Z;        %branch admittance

for n = 1:nbr

if a(n) <= 0  a(n) = 1; else end

Ybus=zeros(nbus,nbus);     % initialize Ybus to zero

% formation of the off diagonal elements

for k=1:nbr;

       Ybus(nl(k),nr(k))=Ybus(nl(k),nr(k))-y(k)/a(k);

       Ybus(nr(k),nl(k))=Ybus(nl(k),nr(k));

    end

end

% formation of the diagonal elements

for  n=1:nbus

     for k=1:nbr

         if nl(k)==n

         Ybus(n,n) = Ybus(n,n)+y(k)/(a(k)^2) + Bc(k);

         elseif nr(k)==n

         Ybus(n,n) = Ybus(n,n)+y(k) +Bc(k);

         else, end

     end

end

basemva = 100;  accuracy = 0.01; maxiter =3;

ns=0; ng=0; Vm=0; delta=0; yload=0; deltad=0;

nbus = length(busdata(:,1));

for k=1:nbus

n=busdata(k,1);

kb(n)=busdata(k,2); Vm(n)=busdata(k,3); delta(n)=busdata(k, 4);

Pd(n)=busdata(k,5); Qd(n)=busdata(k,6); Pg(n)=busdata(k,7); Qg(n) = busdata(k,8);

Qmin(n)=busdata(k, 9); Qmax(n)=busdata(k, 10);

Qsh(n)=busdata(k, 11);

    if Vm(n) <= 0  Vm(n) = 1.0; V(n) = 1 + j*0;

    else delta(n) = pi/180*delta(n);

         V(n) = Vm(n)*(cos(delta(n)) + j*sin(delta(n)));

         P(n)=(Pg(n)-Pd(n))/basemva;

         Q(n)=(Qg(n)-Qd(n)+ Qsh(n))/basemva;

         S(n) = P(n) + j*Q(n);

    end

end

for k=1:nbus

if kb(k) == 1, ns = ns+1; else, end

if kb(k) == 2 ng = ng+1; else, end

ngs(k) = ng;

nss(k) = ns;

end

Ym=abs(Ybus); t = angle(Ybus);

m=2*nbus-ng-2*ns;

maxerror = 1; converge=1;

iter = 0;

% Start of iterations

clear A  DC   J  DX

while maxerror >= accuracy & iter <= maxiter % Test for max. power mismatch

for i=1:m

for k=1:m

   A(i,k)=0;      %Initializing Jacobian matrix

end, end

iter = iter+1;

for n=1:nbus

nn=n-nss(n);

lm=nbus+n-ngs(n)-nss(n)-ns;

J11=0; J22=0; J33=0; J44=0;

   for i=1:nbr

     if nl(i) == n | nr(i) == n

        if nl(i) == n,  l = nr(i); end

        if nr(i) == n,  l = nl(i); end

        J11=J11+ Vm(n)*Vm(l)*Ym(n,l)*sin(t(n,l)- delta(n) + delta(l));

        J33=J33+ Vm(n)*Vm(l)*Ym(n,l)*cos(t(n,l)- delta(n) + delta(l));

        if kb(n)~=1

        J22=J22+ Vm(l)*Ym(n,l)*cos(t(n,l)- delta(n) + delta(l));

        J44=J44+ Vm(l)*Ym(n,l)*sin(t(n,l)- delta(n) + delta(l));

        else, end

        if kb(n) ~= 1  & kb(l) ~=1

        lk = nbus+l-ngs(l)-nss(l)-ns;

        ll = l -nss(l);

      % off diagonalelements of J1

        A(nn, ll) =-Vm(n)*Vm(l)*Ym(n,l)*sin(t(n,l)- delta(n) + delta(l));

              if kb(l) == 0  % off diagonal elements of J2

              A(nn, lk) =Vm(n)*Ym(n,l)*cos(t(n,l)- delta(n) + delta(l));end

              if kb(n) == 0  % off diagonal elements of J3

              A(lm, ll) =-Vm(n)*Vm(l)*Ym(n,l)*cos(t(n,l)- delta(n)+delta(l)); end

              if kb(n) == 0 & kb(l) == 0  % off diagonal elements of  J4

              A(lm, lk) =-Vm(n)*Ym(n,l)*sin(t(n,l)- delta(n) + delta(l));end

        else end

     else , end

   end

   Pk = Vm(n)^2*Ym(n,n)*cos(t(n,n))+J33;

   Qk = -Vm(n)^2*Ym(n,n)*sin(t(n,n))-J11;

   if kb(n) == 1 P(n)=Pk; Q(n) = Qk; end   % Swing bus P

     if kb(n) == 2  Q(n)=Qk;

         if Qmax(n) ~= 0

           Qgc = Q(n)*basemva + Qd(n) - Qsh(n);

           if iter <= 7                  % Between the 2th & 6th iterations

              if iter > 2                % the Mvar of generator buses are

                if Qgc  < Qmin(n),       % tested. If not within limits Vm(n)

                Vm(n) = Vm(n) + 0.01;    % is changed in steps of 0.01 pu to

                elseif Qgc  > Qmax(n),   % bring the generator Mvar within

                Vm(n) = Vm(n) - 0.01;end % the specified limits.

              else, end

           else,end

         else,end

     end

   if kb(n) ~= 1

     A(nn,nn) = J11;  %diagonal elements of J1

     DC(nn) = P(n)-Pk;

   end

   if kb(n) == 0

     A(nn,lm) = 2*Vm(n)*Ym(n,n)*cos(t(n,n))+J22;  %diagonal elements of J2

     A(lm,nn)= J33;        %diagonal elements of J3

     A(lm,lm) =-2*Vm(n)*Ym(n,n)*sin(t(n,n))-J44;  %diagonal of elements of J4

     DC(lm) = Q(n)-Qk;

   end

end

DX=A\DC';

for n=1:nbus

  nn=n-nss(n);

  lm=nbus+n-ngs(n)-nss(n)-ns;

    if kb(n) ~= 1

    delta(n) = delta(n)+DX(nn); end

    if kb(n) == 0

    Vm(n)=Vm(n)+DX(lm); end

 end

  maxerror=max(abs(DC));

end

V = Vm.*cos(delta)+j*Vm.*sin(delta);

deltad=180/pi*delta;

i=sqrt(-1);

k=0;

for n = 1:nbus

     if kb(n) == 1

     k=k+1;

     S(n)= P(n)+j*Q(n);

     Pg(n) = P(n)*basemva + Pd(n);

     Qg(n) = Q(n)*basemva + Qd(n) - Qsh(n);

     Pgg(k)=Pg(n);

     Qgg(k)=Qg(n);     %june 97

     elseif  kb(n) ==2

     k=k+1;

     S(n)=P(n)+j*Q(n);

     Qg(n) = Q(n)*basemva + Qd(n) - Qsh(n);

     Pgg(k)=Pg(n);

     Qgg(k)=Qg(n);  % June 1997

  end

yload(n) = (Pd(n)- j*Qd(n)+j*Qsh(n))/(basemva*Vm(n)^2);

end

busdata(:,3)=Vm'; busdata(:,4)=deltad';

Pgt = sum(Pg);  Qgt = sum(Qg); Pdt = sum(Pd); Qdt = sum(Qd); Qsht = sum(Qsh);

Pgg=abs(Pgg);

  vv=abs(V);

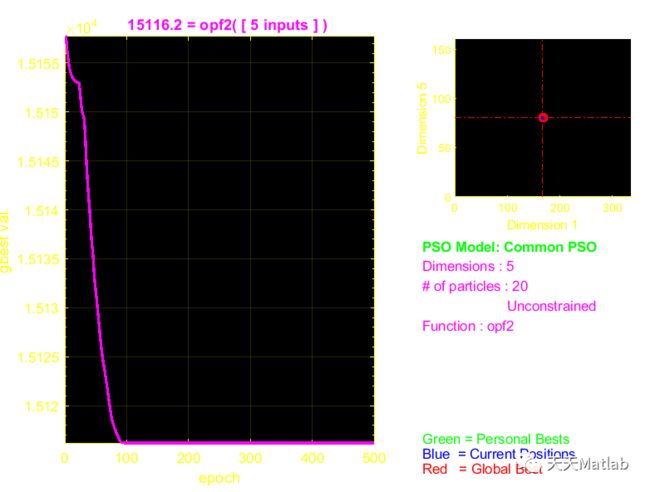
⛄ 运行结果

⛄ 参考文献

[1]郗忠梅, 李有安, 赵法起,等. 基于Matlab的电力系统潮流计算[J]. 山东农业大学学报：自然科学版, 2010(2):4.

⛄ 完整代码

❤️部分理论引用网络文献，若有侵权联系博主删除

❤️ 关注我领取海量matlab电子书和数学建模资料