【图像超分辨率】Understanding Deformable Alignment in Video Super-Resolution

摘要

可变形卷积最初是为适应物体的几何变化而提出的，最近在对齐多个帧方面表现出令人信服的性能，并越来越多地被用于视频超分辨率。尽管其性能显著，但其对准的基本机制仍不清楚。在这项研究中，我们仔细研究了可变形对齐和经典的基于流的对齐之间的关系。我们表明，可变形卷积可以被分解为空间扭曲和卷积的组合。这种分解揭示了可变形配准和基于流动的配准在表述上的共性，但其关键区别在于它们的偏移多样性。我们通过实验进一步证明，可变形配准中增加的多样性产生了更好的配准特征，从而大大改善了视频超分辨率输出的质量。基于我们的观察，我们提出了一个偏移保真度的损失，以指导光流的偏移学习。实验表明，我们的损失成功地避免了偏移量的溢出，缓解了可变形配准的不稳定性问题。除了对可变形配准的贡献外，我们的表述激发了一种更灵活的方法，将偏移多样性引入到基于流动的配准中，提高其性能。

1 引言

视频超分辨率（SR）旨在从其低分辨率的对应帧中恢复高分辨率的连续帧。视频超分辨率的关键挑战在于有效利用相邻帧的互补细节，这些细节可能由于相机和物体的运动而错位。为了建立帧间对应关系，早期的方法（Caballero等人，2017；Liu等人，2017；Sajjadi、Vemulapalli和Brown，2018；Tao等人，2017；Xue等人，2019）采用光流进行明确的帧对齐。他们将相邻的帧扭曲到参考帧，并将这些图像传递给卷积神经网络（CNN）进行超分辨率。再有一些研究（Tian等人，2020；Wang等人，2019a,b）通过可变形卷积隐含地执行对齐操作，并显示出卓越的性能。例如，NTIRE 2019年视频修复挑战赛的获胜者（Nah等人019b,c），EDVR（Wang等人2019b），大大超过了以前的粗到细的可变形卷积方法的形式。

这两种方法一般被认为是正交的方法，是独立发展的。了解（1）显式排列和隐式排列之间的关系，以及（2）隐式建模带来的改进来源，是非常有意义的。由于没有相关的工作，我们通过探索两种代表性方法的内在联系来弥补这一空白–基于流的对齐（用光流进行显式对齐）和可变形对齐（用可变形卷积进行隐式对齐）。研究它们之间的关系不仅有助于我们理解可变形对齐的工作机制，而且还能启发我们对视频SR方法进行更普遍的设计。

可变形卷积（Dai等人，2017；Zhu等人，2019）（DCN）最初是为物体检测中的空间适应而设计的。其关键思想是将标准卷积的采样位置通过一些学习到的偏移量进行置换。当DCN被应用于时间对齐时，相邻帧上的位移内核将被用于对齐中间特征。从表面上看，这个程序与基于流量的方法不同，后者通过流量扭曲来对齐相邻的帧。为了揭示它们之间的关系，我们表明可变形的对齐方式可以被表述为特征级流动扭曲wrap和卷积conv的组合。这种直观的分解表明，这两种对齐方式在本质上有相同的表述，但在其偏移的多样性上有所不同。具体来说，基于流动的对齐方式只在每个特征位置学习一个偏移量，而可变形对齐方式引入了多个偏移量，其数量与DCN的核大小成正比。

在这种关系下，我们系统地研究了偏移多样性的影响，并获得了两个有趣的见解。

1. 首先，在可变形配准中学习到的偏移量具有与光流类似的模式，这表明可变形配准和基于光流的配准在概念和行为上都有很强的相关性。
2. 第二，不同的偏移量比单一的偏移量能达到更好的修复效果。由于不同的偏移集是相互补充的，它们可以有效地缓解闭塞问题，减少大运动引起的扭曲误差。

图1描述了这两种方法在学习偏移量和特征特征方面的比较。

图1：基于流动的对齐（#1）和可变形对齐（#2，#4）中学习到的偏移量与使用基于深度学习的光流估计器（Sun等人，2018）获得的光流（#3）有类似的模式。偏移量的多样性使得变形对准可以学习互补的偏移量（#4），这有效地缓解了闭塞问题，并减少了翘曲误差。因此，可变形对齐后的翘曲特征（#6）比基于流动的对齐（#5）包含更多的细节（见汽车车轮的细节）。

随着对它们的关系有了更深刻的理解，我们决定使用广泛采用的光流技术，以利于可变形卷积的训练。众所周知，**可变形配准的训练是不稳定的，偏移量的溢出会严重降低性能（Wang等人，2019b）。我们提出了一种偏移保真度损失，采用光流来指导DCN的偏移学习，同时保留偏移多样性。**我们的实验表明，提出的策略成功地稳定了可变形配准的训练过程。除了对可变形配准的贡献，我们对DCN的分解也有利于基于流的配准方法。具体来说，在我们的表述中，偏移量的数量不一定等于核大小的平方。与可变形卷积相比，我们的表述为增加基于流动的对齐方法中的偏移集多样性提供了一个更灵活的手段。我们的贡献总结如下。

1. 虽然可变形配准已被证明是传统的基于流动的运动补偿配准的一个令人信服的替代方案，但它与基于流动的配准的联系在文献中仅被浅显地讨论。本文是第一个正式确立了这两个重要概念之间关系的研究。
2. 我们系统地研究了偏移多样性的好处。我们表明，偏移多样性是提高对准精度和SR性能的关键因素。
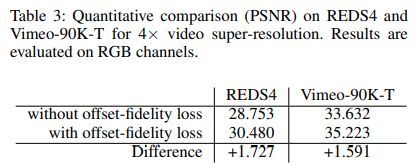
3. 基于我们的研究，我们**在可变形配准中提出了一个偏移保真度损失，以稳定训练，同时保留偏移多样性。**使用我们的损失，可以观察到高达1.7pb的改进。
4. 我们的表述激发了一种更灵活的方法来增加基于流动的对齐方法中的偏移多样性。

2 相关工作

与单幅图像SR不同（Dai等人，2019；Dong等人，2014；Haris，Shakhnarovich和Ukita，2018；He等人，2019；Ledig等人，2017；Lim等人，2017；Liu等人，2020；Mei等人，2020；Wang等人，2018b，a；Zhang等人。2018；Zhang, Gool, and Timofte 2020），视频SR的另一个挑战（Dai等人，2015；Huang, Wang, and Wang 2015；Liu and Sun 2014；Takeda等人，2009；Yi等人，2019；Li等人，2020；Isobe等人，2020a,b）是为构建准确的对应关系而对齐多个框架。根据是否显式估计光流，视频SR中现有的运动补偿方法主要可以分为两个分支–显式方法和隐式方法。

大多数现有的方法都采用显式运动补偿方法。这种方法的早期作品（Kappeler等人，2016；Liao等人，2015）首先使用一个固定的外部光流估计器来估计参考帧和其相邻帧之间的流场，然后学习一个从流场扭曲的输入到高分辨率输出的映射。这种两阶段的方法很耗时，而且当流量估计不准确时往往会失败。一些后续研究（Caballero等人，2017；Liu等人，2017；Sajjadi，Vemulapalli和Brown，2018；Tao等人，2017；Xue等人，2019）将流量估计组件纳入SR管道。例如，TOFlow（Xue等人，2019）指出，在包括视频SR在内的视频增强中，最佳流量是特定任务的，因此，可训练的运动估计组件比固定的运动估计组件更有效。然而，所有这些方法都明确地在图像域中进行流量估计和扭曲，这可能会在图像结构周围引入伪影（Tian等人，2020）。

最近的一些方法隐含地进行运动补偿，并显示出卓越的性能。例如，DUF（Jo等人，2018）为每个像素位置学习了一个上采样滤波器，其他一些方法（Tian等人，2020；Wang等人，2019a，b）将可变形卷积纳入运动补偿。可变形卷积（Dai等人，2017）**能够预测额外的偏移量，为卷积核提供空间上的灵活性。**这与标准卷积不同，后者被限制在一个规则的邻域。TDAN（Tian等人，2020）将可形成的卷积（Dai等人，2017）用于视频SR中的时间对齐。遵循流量估计方法中的结构设计（Dosovitskiy等人，2015；Ranjan和Black，2017；Sun等人，2018），EDVR（Wang等人，2019b）采用了金字塔和级联架构中的可变形对齐，并在视频SR中实现了最先进的性能。

虽然可变形配准和基于流的经典配准乍看之下毫无关联，但它们确实高度相关。在这项研究中，我们深入研究了它们之间的联系。基于我们的分析，我们提出了一个偏移保真度损失，以稳定训练并提高可变形对齐的性能。

3 统一可变形和基于流的配准

3.1 可变形卷积的重新审视

我们首先简要回顾一下可变形卷积（DCN）（Dai等人，2017），它最初是为了适应物体检测（Bertasius, Torresani, and Shi 2018）和图像分割（Dai等人，2017）任务中物体的几何变化而提出来。让pk是核大小为n×n的标准卷积中的第k个采样偏移。例如，当n=3时，我们有pk∈{（-1，-1），（-1，0），- -，（1，1）}。我们用∆pk表示在位置p+pk的第k个额外的学习偏移。一个可形成的卷积可以被表述为。

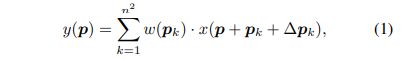
其中x和y分别代表输入和输出特征。如图2(a)所示，与标准卷积不同，可变形卷积有更灵活的采样位置。

图2：3×3核的变形卷积可以分解为9个空间翘曲和一个三维卷积。核的权重用w来表示。

在实践中，我们可以把C通道的特征分为G组，每个空间位置学习n个2×G的偏移量。在DCNv2（Zhu等人，2019）中，引入了调制掩码，以进一步加强对空间支持区域的操作能力。关于调制掩码的详细分析见A.5节。

3.2 可变形配准

在视频SR中，在连续帧之间建立对应关系以进行细节提取和融合至关重要。最近的研究（Tian等人，2020；Wang等人，2019a,b）应用可变形卷积进行特征对齐，超越了传统的流动扭曲方式，如图3所示。

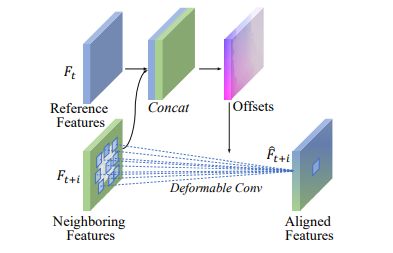
图3：可变形配准应用可变形对齐将相邻特征与参考特征配准。通过对参考特征和相邻特征的几次卷积，预测偏移量。参考特征仅用于预测偏移量，而不直接参与卷积。

让Ft和Ft+i分别为参考帧和相邻帧的中间特征。在可变形配准中，使用可变形卷积将Ft+i与Ft配准，在数学上，我们有。

其中Fˆ t+i代表对齐的特征。偏移量∆pk是通过几个卷积来预测的，Ft和Ft+i都是输入。参考特征仅用于预测偏移量，并不直接参与卷积。

3.3 可变形配准和基于流动的配准之间的关系

可变形配准和基于流动的配准之间有一个直观但不太明显的联系。这种联系在以前的工作中很少被讨论。在本文中，我们没有把它们当作正交的方法，而是统一了这两个重要的概念。接下来，我们通过展示DCN可以被分解为空间扭曲和标准卷积来讨论可变形对齐和基于流动的对齐之间的联系。设x为输入特征，pk+∆pk（k=1，—，n2）为位置p的第k个偏移量。从公式（1），我们有：

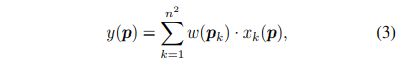
这相当于一个1×1×n 2的标准三维卷积。因此，我们看到，内核大小为n×n的可变形卷积相当于n 2个单独的空间扭曲，然后是内核大小为1×1×n 2的标准三维卷积。图2(b)所示为说明。

备注：

1. 通过在公式(3)中用N∈N代替n 2，该分解通过消除每组内的偏移数必须等于n 2的约束来概括DCN。因此，在剩下的章节中，我们用N表示每组的偏移数。
2. 通过在通道维度上堆叠N个翘曲的特征，1×1×N的三维卷积可以被实现为1×1的二维卷积。换句话说，DCN相当于N个独立的空间翘曲，然后再进行1×1的二维卷积。

从公式（3）中，我们看到，n=1的特殊情况相当于空间翘曲后的1×1卷积。在运动补偿的背景下，这种特殊情况对应于基于流动的对齐。换句话说，可变形排列和基于流动的排列有相同的表述，但在偏移的多样性上有区别。

讨论：
前面提到的分析导致了一些有趣的探索。

1. 与基于流动的对齐方式相比，可变形对齐方式在哪里获得了额外的性能？分析指出了偏移多样性，我们在第4节的实验中验证了这个假设。
2. 更高的偏移多样性是否总是更好的？我们在第4.2节中证明，尽管一般来说，输出质量随着偏移量的增加而增加，但当偏移量越大时，就会出现性能瓶颈。因此，增加偏移量肯定会降低模型的效率而没有明显的性能增益。在实践中，我们应该通过选择一个合适的偏移量来平衡性能和计算效率。
3. 我们可以增加基于流动的对齐的偏移多样性吗？与可变形配准不同，在可变形配准中，偏移量必须等于核大小的平方，而我们的表述将可变形配准泛化为任意数量的偏移量。因此，它提供了一个更灵活的方法，将偏移的多样性引入到基于流量的对齐中。 我们在实验中表明，增加偏移量多样性有助于基于流量的网络实现更好的SR性能。

3.4 偏移保真度损失

在本节中，在第3.3节所示的分解的激励下，我们展示了光流如何通过新提出的偏移保真度损失使可变形对齐受益。

由于其不明确的偏移可解释性，可变形配准通常是通过随机初始化从头开始训练。随着网络容量的增加，可变形配准的训练变得不稳定，偏移量的溢出严重地降低了模型的性能1。相比之下，在基于流动的对准中，各种训练策略被开发出来，以提高对准精度和收敛速度，如采用流动网络结构（Haris, Shakhnarovich, and Ukita 2019; Xue et al. 2019），流动引导损失（Liu et al. 2017），以及流动预训练（Caballero et al. 2017; Tao et al. 2017; Xue et al. 2019）。

鉴于第3.3节中讨论的空间扭曲和可形成卷积之间的关系，我们建议使用光流来指导偏移的训练。具体来说，我们提出了一个偏移保真度损失来约束偏移，使其不太偏离光流。此外，为了便于学习视频SR的最佳和不同的偏移量，我们加入了Heaviside阶梯函数。更具体地说，我们对数据拟合损失进行了如下扩充

其中L是数据拟合损失（例如(Wang et al. 2019b)中的Charbonnier损失），

其中i, j表示空间指数，H（-）表示Heaviside步骤函数。这里λ和t是控制偏移量的多样性的超参数。如第4.3节所示，我们的损失能够稳定训练并避免大型模型的偏移溢出。

4 分析

我们进行实验来揭示视频SR中的可变形排列和基于流的排列之间的联系和区别。除非特别说明，否则我们采用EDVR-M2进行分析，因为它在训练效率和性能之间保持了良好的平衡。此外，为了解开可变形配准中不同成分之间的复杂关系，我们在第4.1节和第4.2节中使用了一个非调制的DCN。每个实验的细节都在A.1节中提供。

4.1 可变形配准与光流的对比

通过设置G=N=1（即组=1，每组的偏移数=1），可变形配准所学到的偏移与基于流的配准方法中的光流所捕获的偏移相似。具体来说，当只有一个偏移集需要学习时，该模型会自动学习基于帧间运动的特征对齐。如图4所示，学到的偏移量与PWC-Net（Sun等人，2018）估计的光流高度相似。

尽管它们的相似度很高，但由于任务性质的根本区别，学习到的偏移量和光流之间的差距是不可忽略的（Xue等人，2019）。具体来说，虽然PWC-Net被训练来描述帧之间的运动，但我们的基线是为视频SR训练的，其中光流可能不是帧对应关系的最佳代表。从图4中，我们可以看到，由学习到的偏移量翘起的图像明显保留了更多的场景内容。相比之下，在用光流扭曲的图像中，可以看到一个黑暗区域和一个重影区域。请注意，偏移量是为扭曲特征而学习的，图4中的扭曲图像只是为了说明问题。

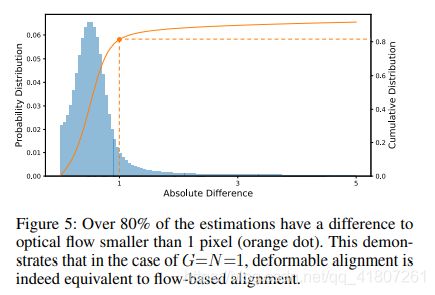
我们通过计算它们的像素差来定量研究偏移集和光流之间的关联性。如图5所示，超过80%的估计与光流的差异小于一个像素。这表明，在G=N=1的情况下，可变形配准确实与基于光流的配准高度等效。在下面的分析中，我们将采用这个模型作为我们接近基于流动的对准基线。

特征翘曲：前面提到的基于流程的对齐基线会进行特征扭曲。这与大多数基于流的方法不同，这些方法学习流用于图像翘曲（Liu等人，2017；Xue等人，2019）。在这些方法中，流量包含分数值，因此在翘曲期间需要插值。这不可避免地引入了信息损失，特别是高频细节。因此，模糊的对齐图像产生次优的SR结果。**最近的可变形配准方法（Tian等人，2020；Wang等人，2019a，b）试图在特征水平上进行配准，并取得了显著的效果。**我们通过用图像对齐模块取代我们基于流程的基线中的特征对齐模块来检查特征级翘曲的贡献。令人惊讶的是，尽管结构接近，图像对齐导致了0.84dB的下降。这表明，特征级的翘曲对基于流程的对齐是有益的。更多的比较显示在A.3节。

4.2 偏移量

多样性分解的等效性

在这一节中，我们用第3.3节中的分解来代替DCN，因为它提供了一个更灵活的偏移数量的选择。为了验证它们的等效性，我们训练了两个实例–原始DCN和我们的分解。如表1所示，我们的实验表明，这两个实例取得了类似的性能，证实了我们的假设。

学习的偏移量

鉴于基于流的对齐和可变形对齐的主要区别在于偏移量N的数量，我们很自然地质疑可变形对齐中额外偏移量的作用和特点（即N>1）。为了回答这个问题，我们固定G=1并比较N=1和N=15情况下的性能。

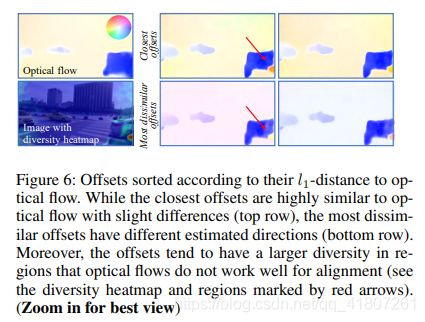
我们根据15个偏移量与光流的l1距离对其进行排序，图6中显示了一个例子。一方面，存在着与光流非常相似的偏移。另一方面，有些偏移与光流相比具有不同的估计方向；尽管这些偏移也能像光流一样分离不同物体的运动，但它们的方向并不符合实际的摄像机和物体的运动。

我们进一步观察偏移量的多样性，这是由偏移量的像素标准偏差来衡量的。我们观察到，在光流不能很好地对准的区域，偏移往往有较大的多样性。例如，如图6的热图所示，在图像边界，标准偏差往往较大，在那里未见过的区域很常见。虽然得到了一组具有不同估计方向的多样化的关集，但它们在整体形状上都与光流类似。这表明在可变形配准中，帧之间的运动仍然是一条重要的线索，就像在基于流动的配准中一样。更多的定性结果见第A.2节

多样性的贡献

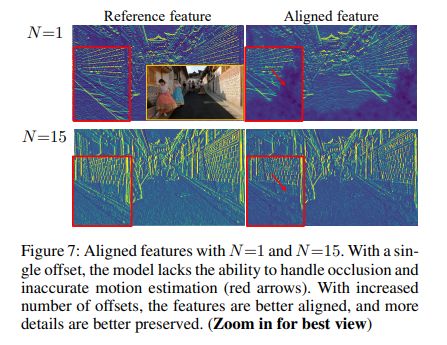
我们还对多样化的流状偏移是否对视频SR有益感兴趣。这促使我们去检查对齐的特征和相应的性能。在单一偏移的情况下，对齐的特征会受到由未见过的区域和不准确的运动估计所引起的扭曲误差的影响。**不准确的对齐特征不可避免地阻碍了信息的聚合，因此损害了后续的修复。相反，在多个偏移的情况下，独立扭曲的特征是相互的，并在融合过程中提供更好的对齐特征，因此缓解了单一偏移的不准确对齐问题。**图7中显示了两个对齐的特征的例子。可以看出，在单一偏移的情况下，对齐的特征不太一致。例如，在图像边界，即对应于不存在于相邻帧的区域，通过单一偏移而扭曲的特征包含一个大面积的黑暗区域。相反，如果有15个偏移量，互补的翘曲特征为融合提供了额外的信息，从而使特征更加连贯并保留了更多的细节。

增加偏移量的多样性

然后，我们通过逐步增加偏移量来考察性能的提高，并试图考察更多的偏移量是否总是能带来更好的性能。

图8和图9分别显示了不同N的定性和定量比较。特别是，随着偏移量从1增加到5，PSNR迅速增加。当N进一步增加时，PSNR达到了约30.23dB。这一结果表明，当偏移量变大时，性能达到一个高峰。因此，简单地增加偏移量可能会降低计算效率而没有明显的性能增益。值得注意的是，由于偏移量必须等于内核大小的平方，因此在可变形对齐中平衡性能和计算效率是不可行的。相反，我们的表述概括了具有任意数量偏移的可变形配准，从而为引入偏移多样性提供了一个更灵活的方法。

我们还检查了偏移多样性和PSNR性能之间的关联性。我们通过所有偏移量的像素标准偏差来衡量偏移多样性。如图9所示，模型的性能与偏移量的多样性呈正相关（基于这六个数据点的皮尔逊相关系数=0.9418）。这一结果意味着，偏移量的多样性实际上有助于性能的提高。

为了进一步支持我们的结论，我们还使用TDAN（Tian等人，2020）和基于流量的网络3来测试偏移多样性带来的改善。如表2所示，两个模型的PSNR最多可提高0.23dB。

此外，在基于流的网络中观察到0.18dB的改善，这表明偏移多样性不仅改善了特征对齐，而且在图像对齐中也是建设性的。除了增加偏移量N，偏移多样性也可以通过增加组数G来实现。有趣的是，上述关于N的结论也适用于G。更详细的分析见A.4节。

4.3 偏移保真度损失

我们用官方训练方案训练EDVR-L。随着网络容量的增加，可变形对齐的训练变得不稳定。**如果没有偏移保真损失，在可变形配准后，偏移的溢出会产生一个零特征图。因此，EDVR本质上成为一个单一的图像SR模型。相反，当偏移量偏离光流时，我们的损失会对偏移量进行惩罚，从而产生更多可解释的偏移量和更好的性能。**如图10所示，EDVR能够以较低的训练损失收敛我们的偏移保真度损失。请注意，在图10(a)中，训练损失在大约300K时增加，这也是偏移量溢出的时间。在表3中，我们看到我们的损失引入了高达1.73dB的额外改进。定性结果见A.6节。

5 结论

可变形配准在视频超分辨率中的成功引起了极大的关注。在这项研究中，我们没有涵盖可变形配准和基于流的配准在概念和行为上的内在联系。对于基于流动的对齐，我们的工作放松了可变形卷积对偏移数量的约束。它允许以一种更灵活的方式来增加基于流动的对齐方法中的偏移多样性，提高输出质量。至于可变形对齐，我们的调查使我们能够理解它的基本机制，可能会激发新的对齐方法。在分析的基础上，我们提出了一个偏移保真度损失，以缓解训练期间的稳定性问题。