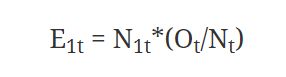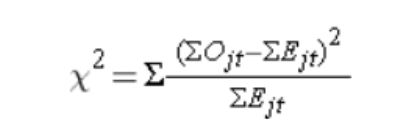生存分析及生存曲线_2021-01-30

生存分析（英文：Survival Analysis），是生物信息学分析中常用到的一种重要方法，主要分析场景如：不同组癌症病人在一种或者一种以上的变量作用下其生存概率随着记录时间发展而发生的变化或者走势。这条曲线（或多条曲线）往往是呈现从高到低（由左到右）的发展趋势，往往最后以病人的死亡事件（death event）而结束，当然这里的事件也可以是肿瘤转移、复发、病人出院、重新入院等任何可以明确识别的事件。

生存分析要解决的核心问题就是各组样品数据在一个或者多个变量作用下它们生存概率随着观测时间如何发展（变化）以及它们之间的可比性。

要解决这两个主要问题：（1）各自变化；（2）之间比较

再此之前，说明几个概念：

（1）生存概率（Survival probability），指的是研究对象从试验开始直到某个特定时间点仍然存活的概率，可见它是一个对时间t的函数，定义之为 S(t)；

（2）风险概率（Hazard probability ），指的是研究对象从试验开始到某个特定时间 t 之前存活，但在 t 时间点发生观测事件如死亡的概率，同样，它也是对时间 t 的函数，定义为 H(t)。

接下来要讲的 Kaplan-Meier 生存概率估计主要关注 S(t)，而后面讲到的 Cox 风险比例模型则关注 H(t)。

（3）数据删失（Censored Data），是指生存分析记录过程中发生数据记录丢失或者无法记录的情况

主要由以下原因造成的：

失访：指失去联系；

退出：死于非研究因素或非处理因素而退出研究；

终止：设计时规定的时间已到而终止观察，但研究对象仍然存活。

数据删失类型有：

右删失(Right Censoring)：只知道实际寿命大于某数；

左删失(Left Censoring)：只知道实际寿命小于某数；

区间删失(Interval Censoring)：只知道实际寿命在一个时间区间内。

需要引入统计学方法：包括：

1.寿命表（Life Table）

表格统计：

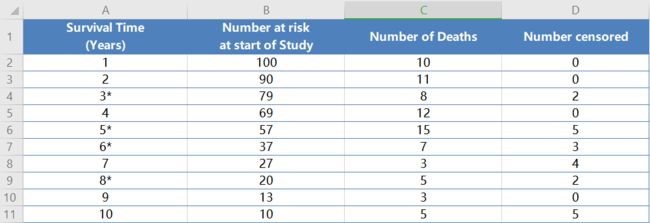
A 列是从生存试验开始起，持续的观测时间，星号代表在该时间有删失数据发生；

B 列是指在 A 列对应的时间开始之前所有存活的研究对象个数，也可以叫做 at risk 的人数，表示当前具有死亡风险的有效人群，是排除了已经死亡和删失的数据之后剩余的人数；

C 列为恰好在 A 列对应的时间死亡的人数；

D 列即表明在该时间点删失的个数。

第一行则可以解读为，在 1年这个时间点之前，本来有 100个患者，在 1 这个时间点（或其之后的一小段时间区间）死亡了10个人，没有删失数据，意味着还剩 90 人；

随后，只要有新增死亡或删失数据，则在表中新建一行，记录时间和人数。

所以紧接着第二行可以解读为，在2年这个时间点之前，at risk at start of study人数为90人，在2这个时间的死亡了11人，没有删失数据，还存活79人；再随着时间发展继续记录：第三行3*，说明这一个时间点是有数据删失情况发生的，在3年这个时间点之前，at risk人数为79人，然后在3年这个时间点死亡了8人，数据删失有两人，这个两个人可能为：失访、退出或者终止。

这个生存分析寿命表一直记录下去，直到试验结束。于是我们就有了试验数据。

2.Kaplan-Meier 生存概率估计（Kaplan-Meier survival estimate）

下面是Kaplan-Meier公式：

Kaplan-Meier生存曲线的生存率公式如下，生存概率 S(ti) 等于上一个时间点 i-1 的生存概率乘以1与di/ni差值的乘积，ni是ti点前存活总人数，di是事件在ti发生数目，ti 表示第 i 个时间点。S(ti-1) 表示在上一个时间点 i-1 的生存概率。

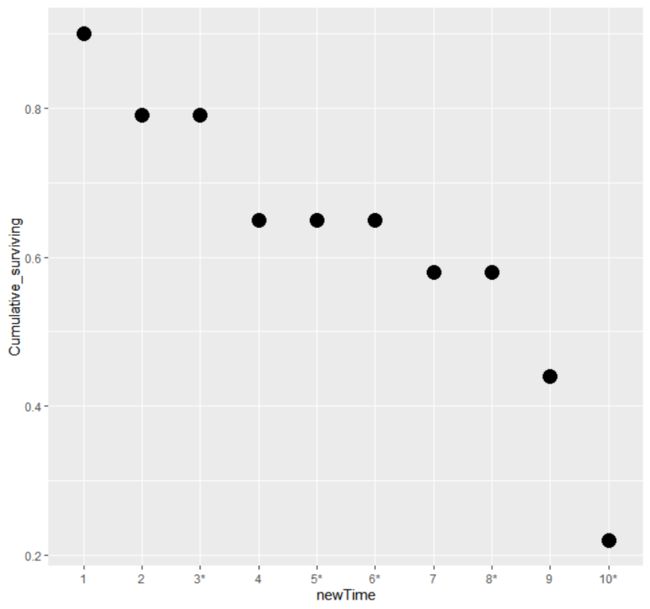
我们利用公式计算一下实例数据的ti时间点不死亡概率（E列）以及累积的生存概率（F列）如下表：

 

该表中  E 列即不死亡概率，F 列则表示累积的生存概率，可以看到随着时间增加，死亡人数增多，越到后期，生存概率越低，这是符合常理的。另外需要注意，在删失发生时，生存概率时没有变化的。

 

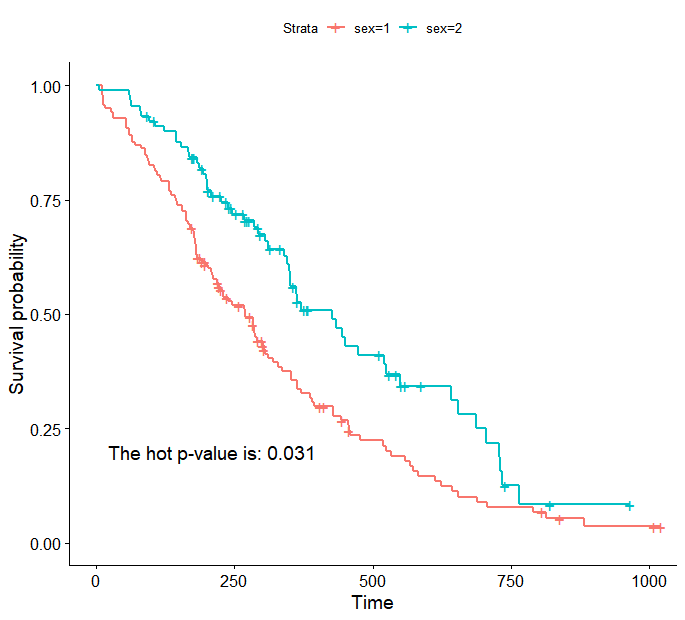
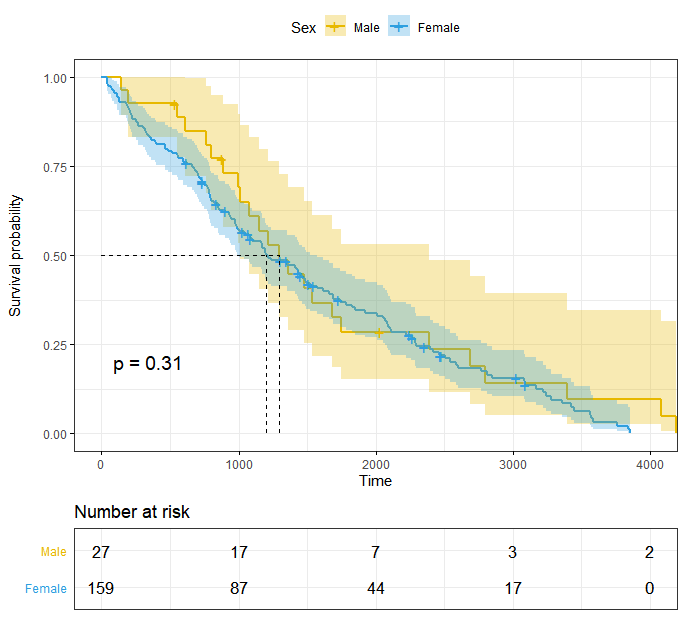
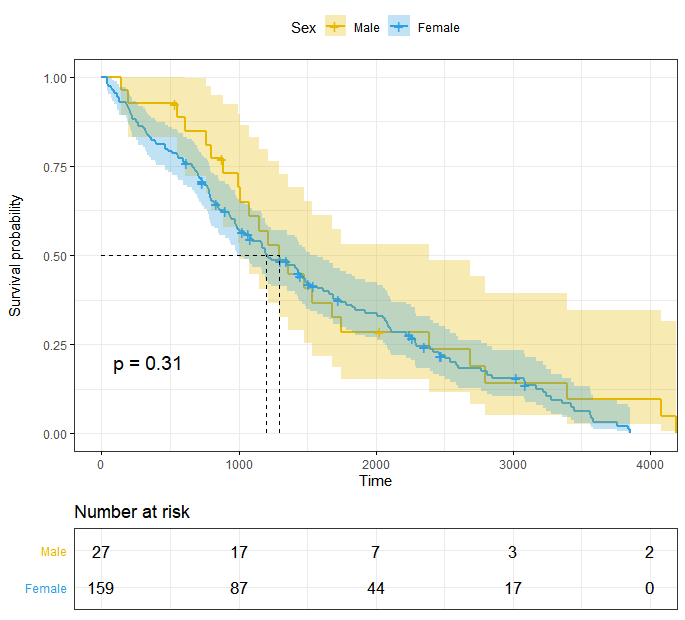
通常生存曲线是多条线的，生存曲线（Survival curve）如下图所示：

上图测试数据绘制的生存曲线，红色线为性别代码1分组，蓝宝石色为性别代码为2分组，不同组别对应的中位生存时间不同，可以一定程度上反应出不同组别死亡风险的不同。这是解决了各组如何变化的问题。那么如何比较二者之间差异是否显著呢？一般我们可以采用 Logrank 统计方法来对生存数据进行统计分析。

3.Logrank检验 和 Breslow 检验（Wilcoxon 检验）

Logrank 方法是由 Nathan Mantel 最初提出的，它是一种非参数检验，中文翻译为对数秩检验，主要用来比较两组样本的生存时间分布的差异。

Logrank 检验的零假设是指两组的生存时间分布完全一致，当我们通过计算拒绝零假设时，就可以认为两组的生存时间分布存在统计学差异。我们可以通过以下公式计算某组病人在某个时间点的期望死亡人数：

 

其中 E1t是指第一组中，在时刻 t，期望死亡人数；

N1t 指第一组中 t 时刻 at risk的人数，即 t 之前的存活人数；

Ot则指两组（第一组和第二组）总的观测到的实际死亡人数；

Nt 指两组总的 at risk 的人数，或 t 时间之前两组的总人数。

有了每个时间点的死亡期望值之后，我们构造如下的卡方值：

 

这里分子上的 ΣOjt 是指在 j 组所有时间点的观测死亡人数相加之和，是对不同时间点 t 对应的观测值的一个累加，比如 t 分别对应 1 天、2 天、3 天等等；ΣEjt 是指在 j 组所有时间点期望死亡人数相加之和。观测人数和期望人数的差值，就代表了实际情况与我们假设情况是否一致，如果假设是对的，即不同组的生存时间分布是完全一致的，那么观测人数和期望人数的差值会是非常小的。因为差值有正有负，所以对它取平方，这样就不会出现抵消的情况。

再加一个分母即 ΣEjt，相当于转换成百分比；最后把不同组别得到的值加起来，就得到 X2 值。通过查表可根据 X2 值来判断是否需要拒绝零假设。

介绍完 Logrank 检验之后，我们再介绍另一种方法：Breslow 检验，其实也就是 Wilcoxon 检验，与 Logrank 不同的是，在每个时间点统计观测人数和期望人数时，他会给它们乘以一个权重因子，即当前时间点的 at risk 的总人数，然后再把所有时间点加起来去统计卡方值。

可以想象随着时间点越靠后，at risk 的总人数会越小，因此权重越少，对 X2 值的贡献就越小。因此 Breslow 检验对试验前期的差异要更加敏感，而相对来说 Logrank 对后期相对更敏感一些，因为它的所有时间点的权重参数都是1。

在实际使用中，我们可以使用不同的方法从多个角度对数据去进行探究。

4.Cox 比例风险回归模型

Cox比例风险回归模型（Proportional l Hazards Regression analysis 或 Cox Proportional-Hazards Model），Cox 模型是一种半参数模型，因为它的公式中既包括参数模型又包括非参数模型。简单说下参数模型和非参数模型的相同与区别。相同点是它们都是用来描述某种数据分布情况的；不同点在于，参数模型的参数是有限维度的，即有限个参数就可以表示模型分布，比如正态分布里的均值和标准差；而非参数模型的参数则属于某个无限维的空间，无法用有限参数来表示，Cox模型公式如下：

 

其中 t 是生存时间，x1, x2 到 xp 指的是具有预测效应的多个变量，b1, b2到 bp则是每个变量对应的 effect size 即效应量，可以理解为结果的影响程度，后面会解释。h(t) 就是不同时间 t 的 hazard，即风险值。而 h0(t) 是基准风险函数，也就是说在其他协变量 x1, x2, …, xp 都为 0 时，即不起作用时，衡量风险值的函数。

根据公式我们可以看到指数部分是参数模型，因为其参数个数有限，即b1, b2到 bp，而基准风险函数 h0(t) 由于其未确定性，可根据不同数据来使用不同的分布模型，因此是非参数模型。所以说, Cox 模型是一种半参数模型。

h(t) 首先是基于时间变化的，t 是自变量；对于某个病人，不同时间的死亡风险是不一样的，这非常好理解，肿瘤病人肯定是随着病程的进展，复发率、死亡率都会不断提高。我们可以回忆以下之前做 Kaplan-Meier 的那个表格，在最后的时间点生存率也越来越低，意味着风险越来越高。其次除了时间，不同年龄、性别、血压等指征不同的病人，死亡风险也不一样。

比如这次的新冠病毒 Covid-19，年纪越大致死率越高，这也就是为什么 Cox 模型要把诸多可能影响生存率的因素都当作协变量引入到公式中去，在该公式中即 x1, x2, …, xp。我们的主要目标是通过一定方法来找到合适的 h0(t)，以及所有协变量的系数 b1, b2, …, bp。实际上cox 模型是需要用到极大似然估计等计算方法，首先构建特定的似然函数，通过梯度下降等方法来求解模型的参数，使得函数求解值最大。

5.complementary log-log plot

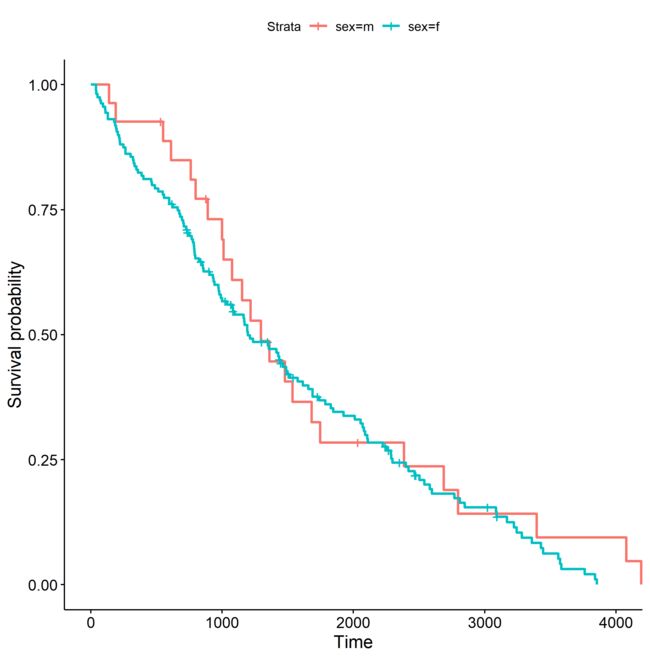
既然不同人之间的风险比例固定，那么一个最简单的例子就是任意分组情况下，两组的 Kaplan–Meier 曲线不应该相交叉，如果曲线相交叉，说明两组的生存概率关系随事件发生了变化，亦即风险比随时间发生变化，与假设相悖。如下图所示：

 

然而，在实际应用中，由于样本量较小时，生存曲线会引入较大的误差，因此该判断方法有可能失效。一个更加复杂的方法为 complementary log-log plot，感兴趣的同学可以搜索学习；对于生存分析 ，除了 Cox 模型外，还有一些其他可用的参数模型。与 Cox 模型不同，这些参数模型往往给定了可能的风险函数分布，比如指数分布、Weibull 和 Gompertz 分布，然后进一步去估计对应的模型参数。而 Cox 模型只能得到有限信息，如风险比及其显著性。使用这些全参数模型的缺点也是明显的，即固定的分布不一定能满足实际的数据情况，可能带来更多的误差。再实际使用情况中，可根据不同情况进行选择。

下面谈一下使用医药效果被试试验记录数据进行生存分析R代码方法，已经有大牛实现了分析和绘图方法，理解原理，然后会用就可以了。

library(survival)

library(survminer)

help(package="survival")

print(head(pbc))

# id time status trt      age sex ascites hepato spiders edema bili chol

# 1  1  400      2  1 58.76523  f      1      1      1  1.0 14.5  261

# 2  2 4500      0  1 56.44627  f      0      1      1  0.0  1.1  302

# 3  3 1012      2  1 70.07255  m      0      0      0  0.5  1.4  176

# 4  4 1925      2  1 54.74059  f      0      1      1  0.5  1.8  244

# 5  5 1504      1  2 38.10541  f      0      1      1  0.0  3.4  279

# 6  6 2503      2  2 66.25873  f      0      1      0  0.0  0.8  248

# albumin copper alk.phos    ast trig platelet protime stage

# 1    2.60    156  1718.0 137.95  172      190    12.2    4

# 2    4.14    54  7394.8 113.52  88      221    10.6    3

# 3    3.48    210    516.0  96.10  55      151    12.0    4

# 4    2.54    64  6121.8  60.63  92      183    10.3    4

# 5    3.53    143    671.0 113.15  72      136    10.9    3

# 6    3.98    50    944.0  93.00  63      NA    11.0    3

# Create the survival object.

survfit(Surv(pbc$time,pbc$status == 2)~1)

# Call: survfit(formula = Surv(pbc$time, pbc$status == 2) ~ 1)

#

# n  events  median 0.95LCL 0.95UCL

# 418    161    3395    3090    3853

# Plot the graph.

plot(survfit(Surv(pbc$time,pbc$status == 2)~1))

fit <- survfit(Surv(time, status)~sex, data=pbc)

print(fit)

# Call: survfit(formula = Surv(time, status) ~ sex, data = pbc)

#

# 232 observations deleted due to missingness

# n events median 0.95LCL 0.95UCL

# sex=m  27    24  1297    1012    2386

# sex=f 159    137  1197    1000    1576

ggsurvplot(fit, data = pbc) # 绘图

 

### Customized survival curves

ggsurvplot(fit, data = pbc,

          surv.median.line = "hv", # Add medians survival

          # Change legends: title & labels

          legend.title = "Sex",

          legend.labs = c("Male", "Female"),

          # Add p-value and tervals

          pval = TRUE,

          conf.int = TRUE,

          # Add risk table

          risk.table = TRUE,

          tables.height = 0.2,

          tables.theme = theme_cleantable(),

          # Color palettes. Use custom color: c("#E7B800", "#2E9FDF"),

          # or brewer color (e.g.: "Dark2"), or ggsci color (e.g.: "jco")

          palette = c("lightblue", "lightgreen"),

          ggtheme = theme_bw() # Change ggplot2 theme

)

 

# Change font size, style and color at the same time

ggsurvplot(fit, data = pbc,  main = "Survival curve",

          font.main = c(16, "bold", "darkblue"),

          font.x = c(14, "bold.italic", "red"),

          font.y = c(14, "bold.italic", "darkred"),

          font.tickslab = c(12, "plain", "darkgreen"))

 

个人水平有限，仍在不断学习中，如有新认识、收获会及时更新博客，欢迎纠错、指正，最后感谢网上牛人的博客分享！