python实现生存分析（Survival Analysis）

目录

一、生存分析

二、生存分析中涉及的基本概念

2.1 生存时间（survival time）

2.2 完全数据（complete data）

2.3 截尾数据（censored data）

2.4 中位生存期（median survival time）

三、Kaplan-Meier生存分析

四、python代码

4.1 数据展示

4.2 基本分析及绘图

4.3 结果图展示具体参考数据

​4.4 P值计算

五、【扩展】六大肿瘤临床试验终点（End Point）

5.1 OS（overall survival）

5.2 ORR（objective response rate）

5.3 PFS（progression-free survival）

5.4 TTP（time to progress）

5.5 DFS（disease-free survival）

5.6 TTF（time to treatment failure）

六、总结

---

一、生存分析

        在医学或者公共卫生研究中，慢性疾病的发生、发展、预后一般不适用于治愈率、病死率等指标来考核，因为其无法在短时间内明确判断预后情况，为此，只能对患者进行长期随访，统计一定时期后的生存或死亡情况以判断诊疗效果；这样的研究往往会产生带有结局的生存时间资料，英文是time-to-event资料。在分析方法上，需要采用生存分析方法。

        也就是说生存分析是将事件的结果（终点事件）和出现这一结果所经历的时间结合起来分析的一种统计分析方法。

参考网站：统计基本功：一文搞懂生存分析 - 知乎 (zhihu.com)

需要注意的是，生存分析考虑了每个观测出现某一结局的时间长短。

二、生存分析中涉及的基本概念

2.1 生存时间（survival time）

生存时间是指终点事件与起始事件之间的时间间隔。例如：服药到痊愈，化疗到缓解，缓解到复发都是起始事件到终点事件。

2.2 完全数据（complete data）

完全数据是从起点到死亡（死于所研究疾病）所经历的时间。

2.3 截尾数据（censored data）

截尾数据也成为删失数据，从七点到截尾点所经历的时间。

截尾原因：失访、死于其它疾病、观察结束时病人尚存活等。

2.4 中位生存期（median survival time）

中位生存期又称为半数生存期，表示恰好有50%的个体尚存活的时间。

中位生存期越长，表示疾病的预后越好。

可以参考生存分析的一些整理笔记_为你千千万万遍z的博客-CSDN博客_生存分析整理的笔记。

三、Kaplan-Meier生存分析

 KM是一种单因素生存分析，主要研究一个因素对于生存时间的影响。

参考网站：Kaplan-Meier生存分析的结果解读和绘制方法 - 简书 (jianshu.com)

四、python代码

4.1 数据展示

TCGA_miRNA_list_data.csv中的部分数据展示如下：

	cancer	OS.status	OS.time	PFI.status	PFI.time	ABCB7	ABL1	ACTL8	ACTN1	ADAMTS20	AIMP1	ANXA2	ANXA5	APPL1	ARHGDIB	AR	ASF1B
TCGA.OR.A5J8	ACC	1	579	1	530	7.7275	12.3192	1.9638	12.3622	0.5002	9.9539	13.619	14.1114	8.8421	12.4622	4.8463	9.3267
TCGA.OR.A5JF	ACC	0	2015	0	2015	8.7154	11.8137	0.471	10.2134	0	10.4891	12.7932	15.3281	9.1116	9.9415	2.3916	7.0048
TCGA.OR.A5JK	ACC	0	1497	0	1497	8.0944	10.819	0	10.3711	1.7173	10.7181	12.1536	14.7757	9.3412	11.8559	3.109	8.5439
TCGA.OR.A5JM	ACC	1	562	1	72	7.3645	11.0318	0.517	10.2582	0	9.4656	13.1636	13.2636	10.197	7.7755	0.517	10.4527
TCGA.OR.A5JS	ACC	0	383	1	166	8.4446	11.5596	0	11.8351	0.4542	9.7703	13.4224	12.5918	10.2101	8.3867	3.5058	9.7868
TCGA.OR.A5JT	ACC	0	907	0	907	8.8605	11.1568	1.7522	9.3632	0.5595	10.3389	11.8216	14.3669	9.9468	9.7996	7.6265	8.2102
TCGA.OR.A5JW	ACC	0	2202	0	2202	9.1595	11.4993	0	10.7717	0	10.0883	12.9915	14.2024	9.6168	9.4701	6.4502	6.7905
TCGA.OR.A5JX	ACC	0	950	0	950	8.2959	11.7674	0	11.1434	0	9.7478	13.5864	14.9823	9.8272	10.6367	5.7249	5.8108
TCGA.OR.A5JY	ACC	1	552	1	75	8.8129	10.4549	0	9.4101	0.5339	9.8266	11.0593	13.4637	10.0421	10.1317	0.9227	10.2351
TCGA.OR.A5JZ	ACC	0	822	1	247	9.0868	11.601	0	8.6487	0	9.7696	12.4461	13.257	10.4706	10.2183	7.4838	8.8595
TCGA.OR.A5K2	ACC	1	994	1	97	8.6595	11.3187	1.4476	10.0858	0	9.7152	13.1982	13.1493	9.4877	10.1085	0	9.5083
TCGA.OR.A5K4	ACC	0	1082	0	1082	9.4482	11.4007	6.3715	7.767	0	10.6308	10.3539	14.0534	10.4871	8.5366	6.8631	10.0056
TCGA.OR.A5K5	ACC	1	498	1	108	7.9171	11.1059	0	10.3746	0	10.3759	11.9872	14.6585	9.3886	8.7219	0	9.4401
TCGA.OR.A5KV	ACC	0	3878	1	1116	8.636	10.8909	1.3463	9.4854	0	10.3376	12.6353	11.909	9.4364	8.1403	2.2799	7.0995
TCGA.OR.A5LB	ACC	1	1204	1	611	9.417	11.648	0	10.5153	0.9505	10.4135	10.6139	14.3498	9.6953	9.1003	3.6618	7.2921
TCGA.OU.A5PI	ACC	0	1171	1	351	8.8054	11.7289	0	12.3959	0.6509	10.3346	11.4677	14.6725	9.5356	9.2949	6.6549	8.0372
TCGA.PK.A5HB	ACC	0	1293	1	213	9.4981	12.3724	2.073	11.6983	0	10.0217	13.6825	12.7971	9.6987	9.8754	4.7794	9.8079
TCGA.4Z.AA7N	BLCA	1	1367	0	1367	8.3384	11.1338	0	12.1579	0	9.7387	13.7235	11.9514	9.964	13.2053	7.1179	8.0355
TCGA.5N.A9KM	BLCA	1	530	1	276	8.2054	8.8837	0	12.2982	0	10.3061	10.7338	9.9268	10.4691	12.82	2.87	7.2103
TCGA.BL.A3JM	BLCA	1	205	1	111	8.6195	10.7479	0	11.7558	1.7924	10.0253	12.0895	12.395	10.8718	9.9779	1.2442	9.9155
TCGA.BT.A20O	BLCA	1	370	1	315	8.7958	11.0329	1.0081	12.6519	3.1017	9.8481	14.5287	13.2981	10.2741	12.9365	2.3349	9.5308
TCGA.BT.A2LD	BLCA	1	623	1	555	7.7771	10.1681	0	11.7599	0	9.4768	16.0552	13.1128	10.009	12.8477	1.8043	9.7329
TCGA.BT.A3PH	BLCA	1	142	1	142	7.8023	10.3221	0	12.0565	0	10.083	13.7521	9.561	10.3849	11.2468	2.276	10.5126
TCGA.CF.A1HS	BLCA	0	382	1	133	8.5652	11.2926	2.1974	13.0882	0	10.1573	14.6172	12.6623	9.9499	10.9656	2.1974	10.2776
TCGA.CF.A27C	BLCA	0	425	0	425	8.0797	9.4013	0	11.6254	0	10.5095	13.5439	7.524	9.7981	12.7456	6.8212	8.7635
TCGA.CF.A3MF	BLCA	0	383	0	383	7.4839	9.873	0	10.608	0	9.9004	12.1214	9.1997	8.5951	12.2715	2.3891	8.8282
TCGA.CF.A3MH	BLCA	0	398	0	398	7.7137	9.5272	1.141	11.3268	0	9.9765	14.7788	11.7197	9.0359	13.1794	3.9508	9.5042
TCGA.CF.A47S	BLCA	0	333	0	333	7.9686	9.9432	0	11.2289	0	10.2102	12.9921	10.1191	9.0368	12.5294	1.4771	7.2587
TCGA.CF.A47T	BLCA	1	385	1	139	7.7271	10.1317	2.816	11.1283	4.0095	10.4699	12.7287	10.4603	9.0441	12.0023	0	9.6026
TCGA.CF.A47V	BLCA	0	379	0	379	7.4576	9.8486	0	11.1743	0	9.6133	12.422	10.8565	8.6283	12.7199	3.1322	9.002
TCGA.CF.A47X	BLCA	0	384	0	384	7.7908	11.2318	0	10.2091	5.5999	10.4919	11.6108	8.2892	10.4258	11.3627	7.3235	6.2421
TCGA.CU.A72E	BLCA	1	413	1	256	9.0609	10.1453	1.159	12.2895	6.1802	10.1412	16.2998	12.6274	10.2745	12.4334	5.9881	9.5979
TCGA.DK.A1AE	BLCA	0	491	1	211	7.4386	11.0133	2.9424	11.454	3.635	10.4769	14.3791	12.2151	10.8594	9.4474	6.9817	10.1378

4.2 基本分析及绘图

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from lifelines import KaplanMeierFitter
ct = ['BLCA']
f = "hsa-miR-1275"
data_Dir = "./data/TCGA/TCGA_miRNA_list_data.csv"
# 读取csv文件
data = pd.read_csv(data_Dir)
print(data.columns)
# 获取只有cancer name为ct列表中癌症名的数据
data = data[data['cancer'].isin(ct)]
# 获取只有参与计算的列数据
data = data.loc[:, ['cancer', 'OS.status', 'OS.time', 'PFI.status', 'PFI.time', f]]
# 填充因子列的缺失值
data[f] = data[f].fillna(0)
# 删除f列为0值或者NA值的行数据
data = data[-data[f].isin([0])]
groups = data[f]
fig, ax = plt.subplots(figsize=(10, 8))
# 根据基因表达量的中位数进行分组
i1 = (groups > np.median(groups))
i2 = (groups < np.median(groups))
# 开始KM分析绘图
kmf1 = KaplanMeierFitter()
kmf1.fit(data['OS.time'][i1], data['OS.status'][i1], label='High expression')
a1 = kmf1.plot()
kmf1.fit(data['OS.time'][i2], data['OS.status'][i2], label='Low expression')
plt.xlim([0, 2000])
plt.xticks([0, 400, 800, 1200, 1600, 2000], fontsize=20)
plt.yticks([0.00, 0.25, 0.50, 0.75, 1.00], fontsize=20)
plt.xlabel('Time(days)', fontsize=30)
plt.ylabel("Overall survival", fontsize=30)
plt.legend(loc='best', frameon=False)
kmf1.plot(ax=a1)
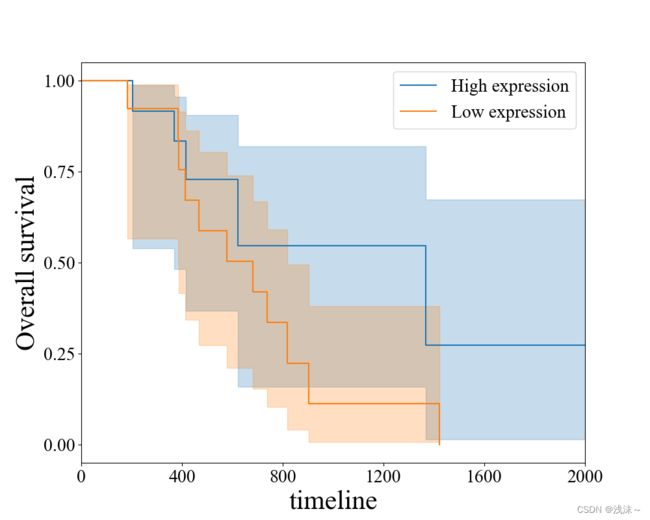
plt.show()
plt.savefig(r"C:\Users\Admin\Desktop\km1.png")

结果图如下：

4.3 结果图展示具体参考数据

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from lifelines.plotting import add_at_risk_counts
from lifelines import KaplanMeierFitter
ct = ['BLCA']
f = "hsa-miR-1275"
data_Dir = "./data/TCGA/TCGA_miRNA_list_data.csv"
# 读取csv文件
data = pd.read_csv(data_Dir)
print(data.columns)
# 获取只有cancer name为ct列表中癌症名的数据
data = data[data['cancer'].isin(ct)]
# 获取只有参与计算的列数据
data = data.loc[:, ['cancer', 'OS.status', 'OS.time', 'PFI.status', 'PFI.time', f]]
# 填充因子列的缺失值
data[f] = data[f].fillna(0)
# 删除f列为0值或者NA值的行数据
data = data[-data[f].isin([0])]
groups = data[f]
# 根据基因表达量的中位数进行分组
i1 = (groups > np.median(groups))
i2 = (groups < np.median(groups))
# 开始KM分析绘图
fig,ax = plt.subplots(figsize=(12,12))
high=KaplanMeierFitter().fit(data['OS.time'][i1], data['OS.status'][i1], label='High expression')
ax = high.plot_survival_function(ax=ax)
low=KaplanMeierFitter().fit(data['OS.time'][i2], data['OS.status'][i2], label='Low expression')
ax = low.plot_survival_function(ax=ax)
plt.xlim([0, 2000])
plt.xticks([0, 400, 800, 1200, 1600, 2000], fontsize=20)
plt.yticks([0.00, 0.25, 0.50, 0.75, 1.00], fontsize=20)
plt.xlabel('Time(days)', fontsize=30)
plt.ylabel("Overall survival", fontsize=30)
plt.legend(loc='best')
add_at_risk_counts(high, low, ax=ax)
plt.tight_layout()
plt.show()
plt.savefig(r"C:\Users\Admin\Desktop\km1.png",dpi=500)

结果图展示如下：

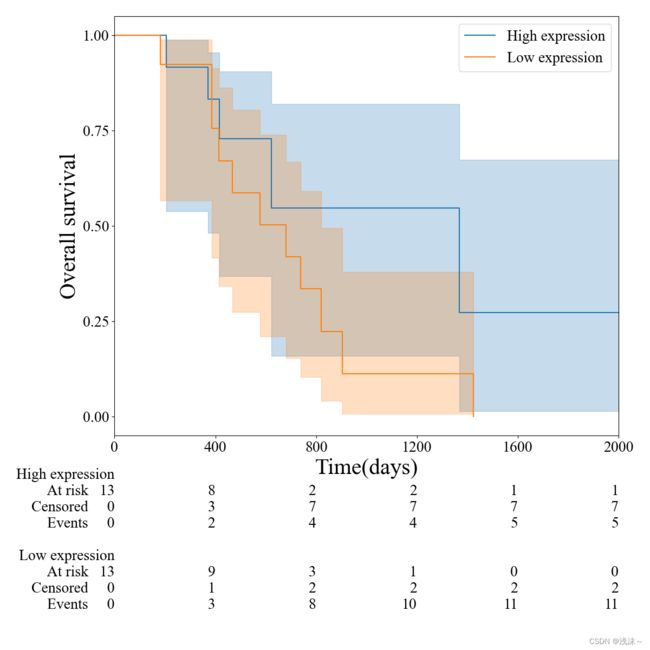 4.4 P值计算

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from lifelines.statistics import logrank_test
ct = ['BLCA']
f = "hsa-miR-1275"
data_Dir = "./data/TCGA/TCGA_miRNA_list_data.csv"
data = pd.read_csv(data_Dir)
print(data.columns)
data = data[data['cancer'].isin(ct)]
data = data.loc[:, ['cancer', 'OS.status', 'OS.time', 'PFI.status', 'PFI.time', f]]
data[f] = data[f].fillna(0)
data = data[-data[f].isin([0])]
groups = data[f]
i1 = (groups > np.median(groups))
i2 = (groups < np.median(groups))
result = logrank_test(data['OS.time'][i1],data['OS.time'][i2],  data['OS.status'][i1],data['OS.status'][i2])
result.print_summary()
print("P_value=",result.p_value)

结果图展示如下：

 更多相关代码可参考网站：python数据分析案例-利用生存分析Kaplan-Meier法与COX比例风险回归模型进行客户流失分析与剩余价值预测_吴下阿泽的博客-CSDN博客写的比较详细。

五、【扩展】六大肿瘤临床试验终点（End Point）

5.1 OS（overall survival）

总生存率：定义为从随机化开始至（因任何原因）死亡的时间。

5.2 ORR（objective response rate）

客观缓解率：定义为肿瘤体积缩小达到预先规定值并能维持最低时限要求的患者比例，为完全缓解和部分缓解比例之和。

5.3 PFS（progression-free survival）

无进展生存率：定义为从随机化开始到肿瘤发生（任何方面）进展或（因任何原因）死亡之间的时间。

5.4 TTP（time to progress）

疾病进展时间：定义为从随机化开始到肿瘤发生（任何方面）进展的时间。

5.5 DFS（disease-free survival）

无病生存期：定义为从随机化开始至疾病复发或（因任何原因）死亡之间的时间。

5.6 TTF（time to treatment failure）

治疗失败时间：定义为：由随机化开始至「退出试验」，退出原因可能是患者拒绝、疾病进展、患者死亡、不良事件等。

参考网址：

1.OS、PFS、DFS 有什么区别？一文搞懂 6 大肿瘤临床试验终点_圈子_医脉通 (medlive.cn)

2.OS/PFS/DFS/DSS各种生存指标傻傻分不清 - 简书 (jianshu.com)

六、总结

1.保存图片设置分辨率的参数为dpi。

2.设置字体大小的参数为fontsize。

3.做KM分析图展示单个具体数据的参数为at_risk_counts=True，也可以直接调用plot_survival_function()函数。

4.做KM分析图展示多个具体数据的参数为add_at_risk_counts()函数。

5.缺失值填充采用fillna函数。

6.上述代码中横坐标设置的是固定的值，所以如果数据过多会导致数据展示不完全，而数据过少又会导致曲线过于集中，也就是曲线长度太短而造成结果展示不太美观，所以横坐标可以通过分组类别的最大值和最小值进行设置。例如：

min_value = min(data[TIME]) - 5
max_value = max(data[TIME]) + 5
plt.xlim([min_value, max_value])
plt.xticks(np.linspace(min_value, max_value, 5), fontsize=23)
plt.yticks([0.00, 0.25, 0.50, 0.75, 1.00], fontsize=23)