JTVAE( Junction Tree Variational Autoencoder )

Junction Tree Variational Autoencoder for Molecular Graph Generation

Year: 2018
Authors: Wengong Jin, Regina Barzilay, Tommi Jaakkola
Journal Name: ICML

Contributions

1. 使用分子图自动设计分子结构
2. 将整个任务分为编码（以连续方法表示分子）和解码（将连续的表示映射回分子图）

Junction Tree Variational Autoencoder

分子图和连接树提供了两个表示 $\mathbf{z}=[{\mathbf{z}}_{\mathcal{T}},{\mathbf{z}}_G]$ ，两者由编码器 $q({\mathbf{z}}_{\mathcal{T}}|\mathcal{T})$ 和 $q({\mathbf{z}}_G|G)$ 产生。两个解码器 $p(\mathcal{T}|{\mathbf{z}}_{\mathcal{T}})$ 和 $p(G|\mathcal{T},{\mathbf{z}}_G)$ 重构分子图。

Junction Tree

已知分子图 $G=(V,E)$ ，连接树为 ${\mathcal{T}}_G=(\mathcal{V},\mathcal{E},\mathcal{X})$ ，其中 $\mathcal{X}$ 为特征字典， $\mathcal{V}=\{C_1,...,C_n\}$ 。 $C_i=(V_i,E_i)$ 为 $G$ 的子结构，满足以下限制

1. ${\cup }_i{V}_i=V$ ， ${\cup }_i{E}_i=E$
2. 如果 $C_k$ 在从 $C_i$ 到 $C_j$ 的路径上， $V_i\cap V_j\subseteq V_k$

Graph Encoder

每个节点 $v$ 和边缘 $(u,v)\in E$ 都有相对应的特征向量 ${\mathbf{x}}_v$ 和 ${\mathbf{x}}_{uv}$ 。定义 ${\mathbf{v}}_{uv}$ 为从 $u$ 到 $v$ 的信息
$${\mathbf{v}}_{uv}^{(t)}=\tau (W_1^g{\mathbf{x}}_u+W_2^g{\mathbf{x}}_{uv}+W_3^g\sum _{w\in N(u)\setminus v}{\mathbf{v}}_{wu}^{(t-1)})$$

其中， $\tau$ 为 RELU ， ${\mathbf{v}}_{uv}^{(t)}$ 表示第 $t$ 轮迭代后的信息， ${\mathbf{v}}_{uv}^{(0)}=0$ 。 $T$ 轮迭代后，将信息聚合为每个节点的隐向量
$${\mathbf{h}}_u=\tau (U_1^g{\mathbf{x}}_u+\sum _{v\in N(u)}{U}_2^g{\mathbf{v}}_{vu}^{(T)})$$

最终的图表示为 ${\mathbf{h}}_G={\sum }_i{\mathbf{h}}_i/|V|$ 。 ${\mathbf{z}}_G$ 从 $\mathcal{N}({\mathbf{\mu }}_G,{\mathbf{\sigma }}_G)$ 中采样， ${\mathbf{\mu }}_G$ 和 $log{\mathbf{\sigma }}_G$ 通过两个独立的仿射层根据 ${\mathbf{h}}_G$ 计算得出。

Tree Encoder

对于每条边缘 $(C_i,C_j)$ ，定义信息向量 ${\mathbf{m}}_{ij}$ 和 ${\mathbf{m}}_{ji}$ 。
$${\mathbf{m}}_{ij}=GRU({\mathbf{x}}_i,\{{\mathbf{m}}_{ki}{\}}_{k\in N(i)\setminus j})$$

GRU 的结构如下所示
$$\begin{gathered} {\mathbf{s}}_{ij}=\sum _{k\in N(i)\setminus j}{\mathbf{m}}_{ki} \\ {\mathbf{z}}_{ij}=\sigma (W^z{\mathbf{x}}_i+U^z{\mathbf{s}}_{ij}+b^z) \\ {\mathbf{r}}_{ki}=\sigma (W^r{\mathbf{x}}_i+U^r{\mathbf{m}}_{ij}+b^r) \\ {\mathbf{m}}_{ij}=tanh(W{\mathbf{x}}_i+U\sum _{k\in N(i)\setminus j}{\mathbf{r}}_{ki}\odot {\mathbf{m}}_{ki}) \\ {\mathbf{m}}_{ij}=(1-{\mathbf{z}}_{ij})\odot {\mathbf{s}}_{ij}+{\mathbf{z}}_{ij}\odot {\mathbf{m}}_{ij} \end{gathered}$$

其中， $\sigma$ 为 sigmoid 函数。信息传递之后，每个节点的隐向量
$${\mathbf{h}}_i=\tau (W^o{\mathbf{x}}_i+\sum _{k\in N(i)}{U}^o{\mathbf{m}}_{ki})$$

采样 ${\mathbf{z}}_{\mathcal{T}}$ 的方法和图编码器类似。

Tree Decoder

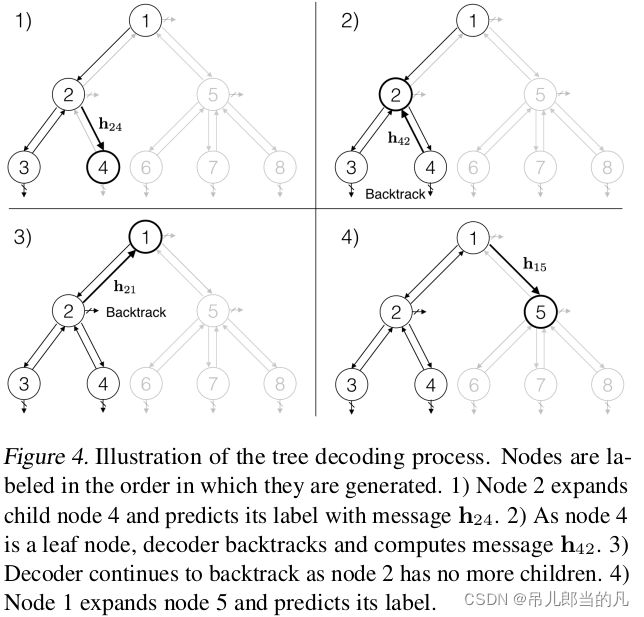
解码过程在原分子的基础上，利用树采样继续扩展新的子结构，原分子的所有子结构均为根节点。
定义 ${\mathcal{E}}_t$ 为到 $t$ 时刻为止已经采样的边缘， ${\mathbf{h}}_{i_t{j}_t}$ 为采样过程中产生的信息。
$${\mathbf{h}}_{i_t{j}_t}=GRU({\mathbf{x}}_{i_t},\{{\mathbf{h}}_{k{i}_t}{\}}_{(k,i_t)\in {\mathcal{E}}_t,k\ne j_t})$$

定义 $p_t$ 为当前叶节点是否继续扩展的概率
$$p_t=\sigma (u^d\cdot \tau (W_1^d{\mathbf{x}}_{i_t}+W_2^d{\mathbf{z}}_{\mathcal{T}}+W_3^d\sum _{(k,i_t)\in {\mathcal{E}}_t}{\mathbf{h}}_{k{i}_t}))$$

定义
$$q_j=softmax(U^l\tau (W_1^l{\mathbf{z}}_{\mathcal{T}}+W_2^l{\mathbf{h}}_{ij}))$$

表示扩展节点 $j$ 的特征 ${\mathbf{x}}_j$ 在特征字典 $\mathcal{X}$ 中的概率。当 $j$ 为根节点时， ${\mathbf{h}}_{ij}=0$ 。训练时采用 teacher forcing 最小化交叉熵损失
$$L_c(\mathcal{T})=\sum _t{L}^d(p_t,{\hat{p}}_t)+\sum _j{L}^l(q_j,{\hat{q}}_j)$$

Graph Decoder

因为相同的树所重构出的图并不唯一，定义 $\mathcal{G}(\mathcal{T})$ 为树 $\mathcal{T}$ 所能重构的图的集合。
$$\hat{G}=\underset{G^{\prime }\in \mathcal{G}(\mathcal{T})}{\mathrm{argmax}}{f}^a(G^{\prime })$$

其中， $f^a$ 为评分函数。出于效率原因，作者按照树本身的解码顺序，一次扩展一个子结构进行计算。
假设根据树节点 $C_j$ 新扩展的子结构为 $C_i$ ，生成了子图 $G_i$ ，子图所对应的向量表示为 ${\mathbf{h}}_{G_i}$ ，评分函数为
$$f^a(G_i)={\mathbf{h}}_{G_i}\cdot {\mathbf{z}}_G$$

定义 $u$ 和 $v$ 为 $G_i$ 中的两个原子。如果 $v\in C_i$ ， ${\alpha }_v=i$ 。如果 $v\in C_j\setminus C_i$ ， ${\alpha }_v=j$ 。设立 ${\alpha }_v$ 是为了标注原子在树中的位置。仿照图编码器，定义 ${\mathbf{\mu }}_{uv}$ 为从 $u$ 到 $v$ 的信息
$$\begin{gathered} {\mathbf{\mu }}_{uv}^{(t)}=\tau (W_1^a{\mathbf{x}}_u+W_2^a{\mathbf{x}}_{uv}+W_3^a{\mathbf{\mu }}_{uv}^{(t-1)}) \\ {\mathbf{\mu }}_{uv}^{(t-1)}=\{\begin{array}{rlr}\sum _{w\in N(u)\setminus v}{\mathbf{\mu }}_{wu}^{(t-1)}& ,& {\alpha }_u={\alpha }_v,\\ {\hat{\mathbf{m}}}_{{\alpha }_u{\alpha }_v}+\sum _{w\in N(u)\setminus v}{\mathbf{\mu }}_{wu}^{(t-1)}& ,& {\alpha }_u\ne {\alpha }_v.\end{array} \end{gathered}$$

计算 ${\mathbf{h}}_{G_i}$ 的方法与图编码器相同。
学习图解码器参数以最大化在每个树节点处预测地面真实图 G 的正确子图 G i 的对数似然
该过程的损失函数为
$$L_g(G)=\sum _i[f^a(G_i)-log\sum _{G_i^{\prime }\in {\mathcal{G}}_i}exp(f^a(G_i^{\prime }))]$$

其中， $i$ 为树的节点， $G_i$ 为正确子图。
以我的理解， $log{\sum }_{G_i^{\prime }\in {\mathcal{G}}_i}exp(f^a(G_i^{\prime }))$ 放大了较大 $f^a(G_i^{\prime })$ 的影响，减少了较小 $f^a(G_i^{\prime })$ 的影响。所以，该损失函数倾向于使正确子图的分数无穷大，错误子图的分数为 0 ，但这样的话 $f^a(G_i)$ 直接使用内积计算相似度是否不太合理？

Results