肯德尔（Kendall）相关系数概述及Python计算例

目录

1. 何谓相关（correlation）?

2. 肯德尔相关 

3. 肯德尔相关的假设

4. 计算公式及代码示例

4.1 Tau-a

4.2  Tau-b       

---

 

1. 何谓相关（correlation）?

        相关是指一种双变量分析（bi-variate analysis）技术，用于分析两个（随机）变量之间相互关联的强度和方向。相关系数的值域范围为[-1,1]，其中绝对值表示相关强度，正负号则表示相关的方向。相关系数为+/-1表示完全的关联。相关系数为0则表示两者完全没有任何关系。

        例1。一般来说，一个人受教育水平越高他的收入就会更高一些（当然这是从统计平均的意义上来说），因此我们可以说收入水平与受教育水平是正相关的。

        例2。一个联赛中各支球队的球员总身价越高，通常球队在联赛中的成绩（排名）就会越靠前，因此我们可以说球员总身价与联赛成绩是正相关的。

        统计学上常用的相关分析有以下几种:

• 皮尔逊相关：Pearson correlation (parametric)
  • 参见皮尔逊相关(Pearson correlation)系数概述及其计算例
• 斯皮尔曼相关：Spearman rank correlation (non-parametric)
  • 参见斯皮尔曼相关(Spearman correlation)系数概述及其计算例
• 肯德尔相关：Kendall rank correlation (non-parametric)
• Point-Biserial correlation.

        本文讨论肯德尔相关（系数）。 

2. 肯德尔相关 

        也称肯德尔秩相关（Kendall Rank Correlation），肯德尔相关系数通常也称为“Kendall’s tau coefficient”，顾名思义，肯德尔相关系数通常用希腊字母来表示（斯皮尔曼相关系数则用来表示，在scipy.stats中两个相关系数计算的函数名kendalltau()和spearmanr()非常清楚地）。 

        与斯皮尔曼秩相关相似的是，肯德尔相关也是一种秩相关系数，是基于数据对象的秩（rank）来进行两个（随机变量）之间的相关关系（强弱和方向）的评估。所分析的目标对象应该是一种有序的类别变量，比如名次、年龄段、肥胖等级(重度肥胖，中度肥胖、轻度肥胖、不肥胖)等。

        不同的是，斯皮尔曼相关是基于秩差（比如说，小明在班级中的历史成绩排名为10，英语成绩排名为4，那么在这个班级的学生的历史成绩和英语成绩的斯皮尔曼相关分析中，小明的成绩的贡献就是(10-4=6) ）来进行相关关系的评估；而肯德尔相关则是基于样本数据对之间的关系来进行相关系数的强弱的分析，数据对可以分为一致对(Concordant)和分歧对(Discordant)。

        比如说变量X的两个样本值记为，与之相对应的变量Y的两个样本值分别记为。

        一致对(Concordant)是指两个变量的这一对样本值取值的相对关系一致，可以理解为与有相同的符号，即；

        分歧对是指这一对样本值取值的相对关系不一致，即。

        当数据样本比较小，而且存在并列排位（tied ranks，比如说小明的历史成绩和英语成绩排名都是第8名）时，肯德尔相关系数是比斯皮尔曼相关系数更合适的一个相关性衡量指标。

 

        适合于采用肯德尔相关系数分析的一些问题例如下所示：

1. 学生的考试成绩分级 (A, B, C…) 和他平均每天学习所投入的时间分级 (<2 hours, 2–4 hours, 5–7 hours…)时间的相关性
2. 顾客满意度 (比如说：非常满意，比较满意，一般。。。) 以及递送时间 (< 30 Minutes, 30 minutes — 1 Hour, 1–2 Hours etc)
3. 。。。

3. 肯德尔相关的假设

        在适用肯德尔相关分析前首先要检查数据是否满足以下基本假设，满足了这些基本假设才能确保你所得到的相关分析结果是有效的。

1. 变量数据是有序的（ ordinal） 或者是连续的（continuous）. 有序尺度（Ordinal scales ）的数据通常用于用数值的方式来衡量非数值的概念，比如说，满意度，幸福度等等，还有像成绩排名啊、比赛名次啊之类的。而连续尺度的数据就勿需解释了，常见的温度啊、体重啊、收入啊等等都（或严格、或近似）算是连续尺度的数据。
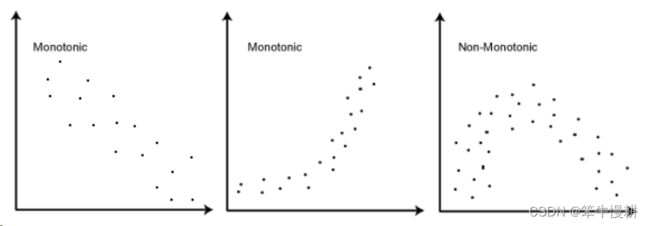
2. 两个变量的数据之间应该遵循单调关系（ monotonic relationship）。 简而言之就是，其中一个变量的值增大，另一个也增大，这个称为正相关；或者一个变量的值增大，另一个就变小，这个称为负相关。当然，这个单调关系是一个统计意义上的，或者说一种趋势上的，而非严格的单调。如下如所示。左图和中图都呈现一种近似单调的关系，而右图则不是，因为右图的左半部分和右半部分的趋势是相反的。

4. 计算公式及代码示例

        肯德尔系数有两个计算公式，一个称为Tau-c，另一个称为Tau-b。两者的区别是Tau-b可以处理有相同值的情况，即并列排位(tied ranks)。下面分别说明这两个公式。

4.1 Tau-a

        

        其中，n表示样本个数。如上所述，肯德尔相关系数是基于数据对来进行分析的，n个样本每两两组队所得到的组队数就是，Tau-a的分母即来自于此。分子中c和d则分别代表一致对和分歧对的个数。

        计算例如下所示：

# Example4 -- Kendall correlation coefficient
from scipy.stats.stats import kendalltau

dat1 = np.array([3,5,1,9,7,2,8,4,6])
dat2 = np.array([5,3,2,6,8,1,7,9,4])
fig,ax = plt.subplots()
ax.scatter(dat1,dat2)
kendalltau(dat1,dat2)

KendalltauResult(correlation=0.3888888888888889, pvalue=0.18018077601410934)

        当然也可以写一段自己的代码来实现相关系数的计算，这样能够更加确切地知道到底是如何计算的，代码示例如下：

c = 0
d = 0
for i in range(len(dat1)):
    for j in range(i+1,len(dat1)):
        if (dat1[i]-dat1[j])*(dat2[i]-dat2[j])>0:
            c = c + 1
        else:
            d = d + 1
k_tau = (c - d) * 2 / len(dat1)/(len(dat1)-1)
            
print('k_tau = {0}'.format(k_tau))    

         运行以上代码同样可以得到0.3888...的结果，只不过没有给出p-value分析结果（这个稍微麻烦一些，此处暂且略过）。

 

4.2  Tau-b       

        在以上Tau-a的计算中假定原始数据中不存在并列排位。当原始数据中存在并列排位时，则用以下公式能够给出更准确的分析结果。

                        

        其中c和d则分别代表一致对和分歧对的个数，和则分别表示数据X中的并列排位个数，和数据Y中的并列排位个数。注意，如果是同时发生在X和Y中并列排位，则既不计入，也不计入。 

# Tau_b
from scipy.stats.stats import kendalltau

dat1 = np.array([3,5,1,6,7,2,8,8,4])
dat2 = np.array([5,3,2,6,8,1,7,8,4])
#dat1 = np.array([3,5,1,9,7,2,8,4,6])
#dat2 = np.array([5,3,2,6,8,1,7,9,4])
c = 0
d = 0
t_x = 0
t_y = 0
for i in range(len(dat1)):
    for j in range(i+1,len(dat1)):
        if (dat1[i]-dat1[j])*(dat2[i]-dat2[j])>0:
            c = c + 1
        elif (dat1[i]-dat1[j])*(dat2[i]-dat2[j])<0:
            d = d + 1
        else:
            if (dat1[i]-dat1[j])==0 and (dat2[i]-dat2[j])!=0:
                t_x = t_x + 1
            elif (dat1[i]-dat1[j])!=0 and (dat2[i]-dat2[j])==0:
                t_y = t_y + 1
                
tau_b = (c - d) / np.sqrt((c+d+t_x)*(c+d+t_y))
            
print('tau_b = {0}'.format(tau_b))            
print('kendalltau(dat1,dat2) =  {0}'.format(kendalltau(dat1,dat2)))

tau_b = 0.6857142857142857
kendalltau(dat1,dat2) =  KendalltauResult(correlation=0.6857142857142857, pvalue=0.011424737055271894)

        注意，这个数据用上面的tao_a的计算方式会得到不同的结果，有兴趣的小伙伴可以自行验证。

 

Kendall Rank Correlation Explained. | by Joseph Magiya | Towards Data Science

scipy.stats.kendalltau — SciPy v1.9.1 Manual