肯德尔相关系数计算方法
肯德尔相关系数计算方法
肯德尔系数可以表示根据两种方法得到的排序的相似程度（注：此方法只能用来表示单个节点在不同评价指标下排序的相似程度）
由影响力传播为例进行说明：
我们设定根据两种评价方法对4个节点（x1,x2,x3,x4）进行排序。
方法1产生的排序结果：{x1,x2,x3,x4}={1，2，3，4}
方法2产生的排序结果：{y1,y2,y3,y4}={2，1，4，3}
则形成元组对：
{(x1,y1),(x2,y2),(x3,y3),(x4,y4)}
改写成列的方式
(x1,y1)
(x2,y2)
(x3,y3)
(x4,y4)
在每个方法的内部构建任意2个元素形成的全排列组合：
{(x1,x2),(x1,x3),(x1,x4),(x2,x3),(x2,x4),(x3,x4)}={(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)}
{(y1,y2),(y1,y3),(y1,y4),(y2,y3),(y2,y4),(y3,y4)}={(2,1),(2,4),(2,3),(1,4),(1,3),(4,3)}
对应位置考察：
第一对：x1
第二对：x1
所以根据肯德尔计算公式：
τ = N c − N d n ∗ ( n − 1 ) / 2 \tau=\frac{N_{c}-N_{d} }{n*(n-1)/2} τ=n∗(n−1)/2Nc−Nd
这里 N c N_{c} Nc表示一致的个数， N d N_{d} Nd表示不一致的个数；n表示网络中节点个数，本文中n表示元素个数。
所以肯德系数 τ = ( 4 − 2 ) 4 ∗ ( 4 − 1 ) / 2 \tau=\frac{(4-2)}{4*(4-1)/2} τ=4∗(4−1)/2(4−2)=1/3=0.33
注意：上面的组合对可以在坐标系中形成点位图，即(x1,y1),(x2,y2)…(xn,yn)
其它的方法可以参见：https://zhuanlan.zhihu.com/p/339077538
可根据上述过程绘制不同方法间的相关图
import numpy as np
import random
import matplotlib.pyplot as plt
# x = np.random.rand(4)
# y = np.random.rand(4)
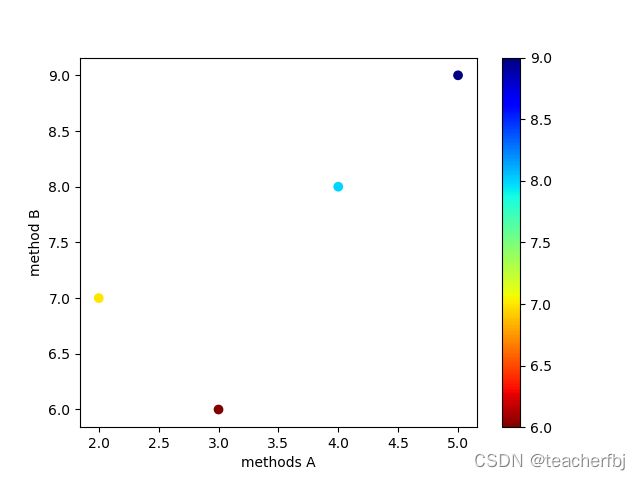
x = [2,3,4,5]
y = [7,6,8,9]
# colors = np.arange(4) #可以换成np.random.rand(4)
colors = y #此处颜色标识为y的数值，使同样值颜色一致，同样可使用当前节点的影响力大小
plt.scatter(x, y, c=colors, cmap='jet_r') #颜色可换 cmap='viridis'
plt.colorbar()
plt.xlabel('methods A') # 横坐标轴标题
plt.ylabel('method B') # 纵坐标轴标题
plt.show()
更复杂散点图可参考：https://zhuanlan.zhihu.com/p/163388220