（DenseNet）Densely Connected Convolutional Networks--Gao Huang

通过全短接实现特征重用和特征数的累计（保证每层产生少量特征数，后面也会concat很多特征，因为叠加了），同时这种全短接可能也加快了损失函数的梯度回传，缓解梯度消失。在DenseBlock内部通过1x1卷积瓶颈降低计算量，在DenseBlock之间的转换层通过“压缩”参数控制输入到下一个DenseBlock的特征数，也能够控制计算量。
所以总上通过特征重用在保证特征数量时，通过瓶颈和压缩降低计算量和参数量，通过实验在相同精度效果下，比其他模型参数量都更小。

但是一个问题是，因为后面的特征要用到前面的特征，所以前面的特征会一直被保存在内存中，所以占用内存是很大的。这也是为什么虽然比ResNet效果好，却不如ResNet流行。（没有实验过是不是内存杀手，这是网上的结论）

0、摘要

最近研究表明，如果CNN在靠近输入和输出的层直接包含更短的连接，可以更深更准确更有效连接。

于是我们设计了本文的DenseNet，它将每层与每层都连接起来，对于有L层的网络，传统CNN有L条连接（包括后续一个连接），但是DenseNet有$\frac{L(L+1)}{2}$条连接。

DenseNet有几个优点：

• 缓解了梯度消失问题
• 加强了特征传播
• 鼓励特征重用
• 大大减少参数量

同时公布了代码和预训练模型：https://github.com/liuzhang13/DenseNet

1、引言

CNN的一个问题是：当输入或梯度信息经过多层达到末端后，可能会“消失”。像 Highway Networks和ResNet都通过短接将信号传递到下一层，还有很多其他形式的网路，但是都有一个关键点：都有从前端层到末端层的短接路径

DenseNet结构如图1所示，与ResNet使用sum对短接整合不同，DenseNet使用concat整合多路特征。

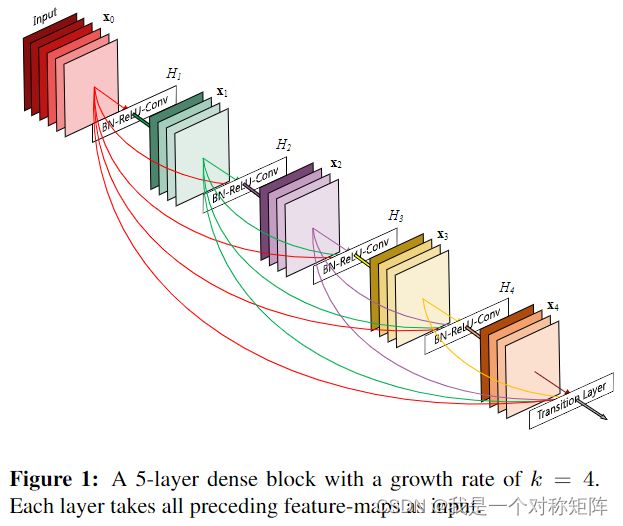
可能一眼看过去觉得DenseNet结构很重，实际上它比普通CNN网络需要更少的参数，因为不需要重新学习冗余的特征映射（个人理解为如果这层需要以前的特征信息，可以直接通过短接拿到。如果是普通CNN则因与前面没有连接所以需要重新学习）。

除此之外，DenseNet的另一大优势是改进了信息流和梯度，每一层都可以直接访问损失函数和初始输入的梯度，这有助于对更深层次的网络体系结构进行培训。

此外作者还观察到稠密链接具有正则化效应，可以减少训练集规模较小的任务的过拟合风险。

2、相关工作（略）

略

3、DenseNets和特性介绍

现在假设有输入图像$x_0$，网络有$L$层，每层实现非线性变换$H_l(\cdot )$，$l$表示第几层。这里的$H(\cdot )$可以是操作的复合函数，也就是可以包含BN层、ReLU、Pooling或者Conv等操作。我们将第$l$层的输出表示为$X_i$

ResNets可以表示为：$X_i=H_i(X_{l-1})+X_{l-1}$

Dense连接可以表示为：$X_l=H_l([X_0,X_1,...,X_{l-1}])$
这里的[ ]表示concat聚合，由于密集的连通性，我们将这种网络结构称为DenseNet

Composite function：为了方便，我们将$H_l(\cdot )$定义为三个连续操作的符合函数：BN+ReLU+Conv

Pooling layers：考虑到特征图在各层的尺寸不同，不能直接concat。如果直接横跨整个也确实不方便，所以将DenseNet划分为多个dense blocks，而块直接的称为转换层，用于卷积和池化，在本文中转换层=BN+1x1Conv+2x2AveragePooling

Growth rate（增长率）：K：如果每个$H(\cdot )$块都生成K个特征通道（不管输入是多少通道，输出都是K通道），则第L层有$K_0+K\ast (L-1)$个输入特征通道，其中$K_0$是输出层的通道数

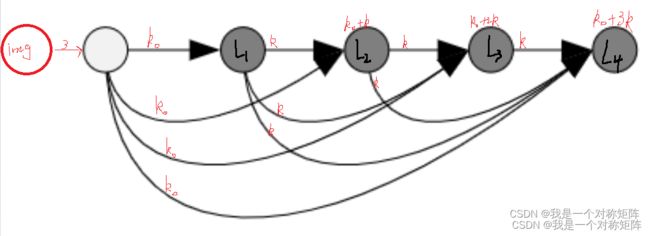
可以发现，实际上每个块的输出通道都是固定为k的，但是输出通道却在不断变多，因为Dense连接的缘故。
可以遇见的是每个块的卷积的个数都可以固定为k（Pytorch：Conv2d(output=k)），而不用像其他网络指定卷积核的个数为128、256、512、1024等特别多，这也是为什么DenseNet实际上参数量很少的缘故，在有限卷积个数通过特征重用也能够有大量的特征数。

在本文中增长率K比较小，但是也有很强的表现，对此的一种解释为每层都可以访问所有前面的特征图，类似网络的全局知识，每个层都将自己产出的K个特征添加到这个全局知识，增长率控制着每一层为全局知识贡献多少信息。一旦全局知识被写入则网络的任何地方都可以访问，与传统网络架构不同，不需要在层层之间复制这种知识（类似不需要你搬运前面的特征，我直接把路给你修好自己去找）。

瓶颈层
尽管每个层（$H(\cdot )$）都只能产生K个输出特征，但是因为累计原因输入特征却有很多。可以在3x3卷积前使用1x1作为瓶颈层减少特征数量。在DenseNet中这样特别有效，鉴于此设计了一个瓶颈版本的DenseNet-B，其$H(\cdot )$=BN-ReLU-Conv(1x1)-BN-ReLU-Conv(3x3)，其中我们让1x1卷积产生4K个特征图

压缩（Compression）：θ

首先明确一点，如图2中，DenseBlock是由多个$H(\cdot )$组成，而转换层是DenseBlock与DenseBlock之间的部分。瓶颈层是用于DenseBlock内的$H(\cdot )$压缩，而压缩是在转换层进行压缩。

为了进一步提高模型的紧凑性，我们可以减少转换层的特征数。如果DenseBlock包含了m个特指数，则后面的转换层产生的特征数为：θm，其中0<θ≤1，显然当θ=1时转换层的输入和输出特征数不变，也就是经过转换层后特征数不变。

我们定义θ<1的DenseNet为DenseNet-C（在实验中我们设置θ=0.5）

如果同时有瓶颈层（DenseNet-B）和θ<1，则称该类型的为DenseNet-BC

实现细节
在除ImageNet之外的所有数据集中，我们使用的DenseNet有三个DenseBlock，每个DenseBlock都有相同的层数。

在进入第一个DenseBlock前，会先经过一个输出通道为16（或者为DenseNet-BC的增长率的两倍）的卷积操作
对于3x3的卷积层，使用zero-padded保证特征图尺寸不变
我们使用1x1卷积+2x2均值池化作为DenseBlock之间的转换层
在最后一个DenseNet，使用全局均值池化+softmax分类器

三个DenseBlock的特征图尺寸是32x32、16x16和8x8（DenseBlock本身不会改变特征图尺寸，所以是转换层导致的尺寸变化）

我们的实验在这几个基础DenseNet上实验（L指层数，见第3节第一句；K指增长率，见第3节Growth rate）：

• $L=40，K=12$
• $L=100，K=12$
• $L=100，K=24$

对于DenseNet-BC：

• $L=100，K=12$
• $L=250，K=24$
• $L=190，K=40$

在ImageNet实验上，我们在224x224的输入上使用有4个DenseBlock的DenseNet-BC结构。最开始的卷积层输出通道为2K（也就是2倍增长率），使用7x7的卷积核大小，stride=2。其他所有层的特征数也是从设置k开始

表1是在ImageNet上的网络结构

4、实验

表2展示DenseNet在几种基准数据集上的效果，并且与最先进的架构进行了比较。可以看到error肯定是DenseNet最好，然后比如DenseNet（K=12）参数量也很少且性能也超过了164层的ResNet。

而且控制K=12就能很好平衡参数量和性能了

ImageNet

表3展示DenseNets在ImageNet数据集上的error

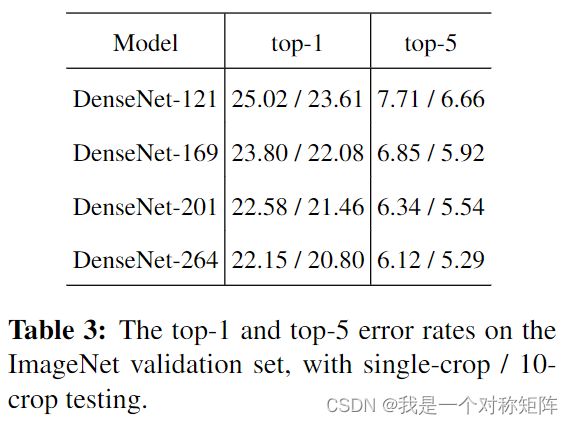
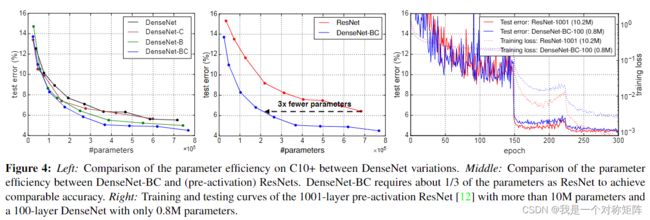
图3展示DenseNet与ResNet的比较，左边是参数量对比右边是FLOPs对比。可以看出相同error下，DenseNet需要的参数量和FLOPs更少

5、一些解释或者结论

隐形深度监督：对于DenseNet可以提高精度的一种解释是，各层通过短节从损失函数接收到额外的监督，可以将DenseNets解读为一种深度监督。深度监督的好处以前已经在深度监督网络(DSN)中显示出来，它的每个隐层都有分类器，强制中间层学习区别性特征。

6、结论

多短接实现特征重用，同时concat实现每层仅产生少量特征数后面也会concat很多通道数

通过1x1卷积瓶颈实现计算量的控制

通过比较在很多数据集上都实现了最优效果，参数量还很小