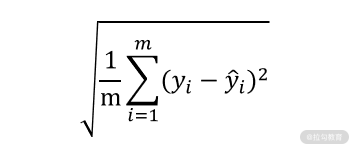数据挖掘思维和实战19 实践 3:使用线性回归预测房价
这次的实践是针对我们的回归算法进行的练习。我们依然从数据获取、模型训练以及效果评估几个步骤来练习,看看如何使用线性回归来预测房价。
数据获取
与我们之前使用的鸢尾花数据集一样,波士顿房价数据集也是一个非常常用的公开数据集。你可以在下面的页面中下载数据。当然,该数据集也被纳入了 sklearn 中,你可以使用 sklearn 中的数据加载方法来获取该数据。
https://archive.ics.uci.edu/ml/machine-learning-databases/housing/
从该页面,我们可以下载两个文件,其中 housing.data 是所有的数据、housing.names 记录了对数据的介绍。
从数据的介绍中我们可以知道,该数据集包含美国人口普查局收集的美国马萨诸塞州波士顿住房价格的有关信息,其中包含了 506 条数据,每条数据有 14 个属性。我们这次要做的就是把前面 13 个当作特征,最后一个房价中位数作为我们要预测的结果。下面的表格里,我列出了每个属性的名称和含义。
| 序号 | 属性名 | 属性含义 |
|---|---|---|
| 1 | CRIM | 人均犯罪率 |
| 2 | ZN | 超过25000平方英尺的规划住宅用地比例 |
| 3 | INDUS | 城镇非零售商业占地 |
| 4 | CHAS | 与查尔斯河之间的距离,在河边为1,不在河边为0 |
| 5 | NOX | 一氧化氮浓度 |
| 6 | RM | 每套住宅平均房间数目 |
| 7 | AGE | 1940年前简称用房的居住率 |
| 8 | DIS | 与波士顿五大商务中心的加权距离 |
| 9 | RAD | 上快速路的难易程度 |
| 10 | TAX | 每一万美元全额财产税的税率 |
| 11 | PTRATIO | 城镇小学教师比例 |
| 12 | B | 计算方法为1000(Bk-0.63)^2,其中Bk小时黑人所占人口比例 |
| 13 | LSTAT | 低收入人群比例 |
| 14 | MEDV | 居住房屋的房价中位数(单位:千美元) |
在代码中,我们首先还是引入我们需要用到的各种包。
from sklearn.datasets import load_boston #波士顿数据集获取方法
import pandas as pd
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from sklearn import metrics
import numpy as np
from sklearn.linear_model import LinearRegression #回归方法
接下来我们看一下数据。这里由于使用 sklearn 可以直接加载数据,所以我就没有使用上面下载的数据。如果你想自己读取和处理数据,也可以直接从下载的文件进行加载。
boston = load_boston()
使用上面的方法加载的数据集就会被存储在“boston”这个变量中,下面我们来看一下这是一个什么类型的数据。
print(type(boston))
输出结果如下,可以看到输出的类型是 sklearn 中的一个类型 Bunch,经过查询我们可以知道 Bunch 实际上是一种字典类型。
那么接下来我们来查看一下该字典中的 key 值都有什么。
print(boston.keys())
输出结果如下,我们可以看到字典的 key 值有 5 个,分别为数据、标签、特征名称、描述和文件名。其中的数据和标签就是两个数组了。
dict_keys(['data', 'target', 'feature_names', 'DESCR', 'filename'])
下面我们把特征名称输出出来看一下。
print(boston.feature_names)
从输出结果我们可以看到跟我最前面介绍的字段名称一样的结果,除了标签字段“MEDV”没有包含在这里面。
['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO' 'B' 'LSTAT']
紧接着我们来看一下数据的规模,我们使用下面这个语句。
print(boston.data.shape)
输出的结果如下,说明 data 字段有 506 行、13 列,这也跟我们之前介绍的一样。
(506, 13)
接下来我们要开始构建训练集和测试集了。先把数据和标签取出来,使用 pandas 的 DataFrame 进行封装。
X = boston.data
y = boston.target
df = pd.DataFrame(X, columns= boston.feature_names)
print(df.head()) #展示头部的几条数据
#以下是输出的结果
CRIM ZN INDUS CHAS NOX ... RAD TAX PTRATIO B LSTAT
0 0.00632 18.0 2.31 0.0 0.538 ... 1.0 296.0 15.3 396.90 4.98
1 0.02731 0.0 7.07 0.0 0.469 ... 2.0 242.0 17.8 396.90 9.14
2 0.02729 0.0 7.07 0.0 0.469 ... 2.0 242.0 17.8 392.83 4.03
3 0.03237 0.0 2.18 0.0 0.458 ... 3.0 222.0 18.7 394.63 2.94
4 0.06905 0.0 2.18 0.0 0.458 ... 3.0 222.0 18.7 396.90 5.33
[5 rows x 13 colum
print(df.info()) #查看数据信息
#以下是输出的信息
RangeIndex: 506 entries, 0 to 505
Data columns (total 13 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 CRIM 506 non-null float64
1 ZN 506 non-null float64
2 INDUS 506 non-null float64
3 CHAS 506 non-null float64
4 NOX 506 non-null float64
5 RM 506 non-null float64
6 AGE 506 non-null float64
7 DIS 506 non-null float64
8 RAD 506 non-null float64
9 TAX 506 non-null float64
10 PTRATIO 506 non-null float64
11 B 506 non-null float64
12 LSTAT 506 non-null float64
dtypes: float64(13)
memory usage: 51.5 KB
None
查看描述功能输出的是对数据集中每个字段的一些统计结果,包括数量、最大最小值、均值、标准差等内容。根据描述方法的结果,可以对每个字段的数据分布有一个大致的了解。
print(df.describe())#查看描述
#以下是输出信息
CRIM ZN INDUS ... PTRATIO B LSTAT
count 506.000000 506.000000 506.000000 ... 506.000000 506.000000 506.000000
mean 3.613524 11.363636 11.136779 ... 18.455534 356.674032 12.653063
std 8.601545 23.322453 6.860353 ... 2.164946 91.294864 7.141062
min 0.006320 0.000000 0.460000 ... 12.600000 0.320000 1.730000
25% 0.082045 0.000000 5.190000 ... 17.400000 375.377500 6.950000
50% 0.256510 0.000000 9.690000 ... 19.050000 391.440000 11.360000
75% 3.677083 12.500000 18.100000 ... 20.200000 396.225000 16.955000
max 88.976200 100.000000 27.740000 ... 22.000000 396.900000 37.970000
看完了具体的数据情况,使用我们前面已经使用过的分割数据集的方法,对数据进行切分,我这里设置的测试集比例为 20%,我们总共有 506 条数据,那么就会有 101 条成为测试集,其余 405 条为训练集,代码如下:
#分割数据集,20%做测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,random_state=0)
模型训练
处理好数据集,接下来就可以进入到模型训练环节了。模型训练的语句很简单,而且训练的速度很快,因为我们的数据量很小。
regressor = LinearRegression() #声明我们的模型
regressor.fit(X_train, y_train) #训练
我们知道,线性回归模型可以根据数据拟合出一条直线,使得损失值最小。既然有一条直线,那一定有截距和斜率,下面我们来看一下我们训练好的模型中,截距和斜率分别是多少。
#查看截距
print(regressor.intercept_)
#输出的截距值如下
38.091694926302125
#查看斜率
coeff_df= pd.DataFrame(regressor.coef_, df.columns, columns=['Coefficient'])
print(coeff_df)
斜率也就是我们的特征系数,所以每一个特征都会有一个系数。如果系数是正的,说明这个属性对房价提升有帮助;如果系数是负的,说明这个属性会导致房价下跌。
Coefficient
CRIM -0.119443
ZN 0.044780
INDUS 0.005485
CHAS 2.340804
NOX -16.123604
RM 3.708709
AGE -0.003121
DIS -1.386397
RAD 0.244178
TAX -0.010990
PTRATIO -1.045921
B 0.008110
LSTAT -0.492793
既然有了截距和斜率,下面我们就可以使用模型来对测试集进行预测了。为了便于了解预测的结果,我们把预测结果和实际的结果一起输出,对照看一下预测的效果。
y_pred = regressor.predict(X_test)
test_df = pd.DataFrame({'Actual': y_test.flatten(), 'Predicted':y_pred.flatten()})
print(test_df)
#输出的结果,第一列是序号 可以不用关注,第二列是实际的结果值,第三列是预测的结果值
Actual Predicted
0 22.6 24.889638
1 50.0 23.721411
2 23.0 29.364999
3 8.3 12.122386
4 21.2 21.443823
.. ... ...
97 24.7 25.442171
98 14.1 15.571783
99 18.7 17.937195
100 28.1 25.305888
101 19.8 22.373233
[102 rows x 2 columns]
还可以使用下面的代码,用条形图的方式来展示对比,这里我们使用 top25 条数据生成条形图。
test_df1 = test_df.head(25)
test_df1.plot(kind='bar',figsize=(16,10))
plt.grid(which='major', linestyle='-', linewidth='0.5', color='green')
plt.grid(which='minor', linestyle=':', linewidth='0.5', color='black')
plt.show()
生成的图像如下,其中蓝色的条纹是实际值,橘红色的条纹是预测值。整体看来,预测值与真实值的差距不大。
效果评估
模型训练好了,预测结果也已经产出了,接下来就进入效果评估阶段。
关于回归模型的效果评估有一些常用的指标,其实我们在前面的课程中也涉及了一点,这里我把几个公式也写在下面了,其实不是很难理解。
MAE(Mean Absolute Error)平均绝对误差。这个很简单,就是把预测值和实际值的差值计算出来然后求平均。
MSE(Mean Squared Error)叫作均方误差。这个应该很熟悉了,在介绍线性回归时,这个就是我们的损失函数。
RMSE(RootMean Squared Error)均方根误差。这个你可能觉得不就是在 MSE 上面开了个根号吗,有什么价值?对于数值来说其实没有太大的区别,但是开根号的作用是让解释性更强,因为 MSE 是平方后的结果。
就拿我们这一课时中预测的房价来说,单位是千美元,平方之后就不好解释了,再开根号就可以让计算单位回到和数据一致的状态。比如下面的结果中,我们就可以说误差是 5.7 千美元。
当然,在 sklearn 中也已经有了封装好的方法供我们调用,具体可以参见下面的代码。
print('MeanAbsolute Error:', metrics.mean_absolute_error(y_test, y_pred))#MAE
print('MeanSquared Error:', metrics.mean_squared_error(y_test, y_pred))#MSE
print('RootMean Squared Error:', np.sqrt(metrics.mean_squared_error(y_test, y_pred)))#RMSE
#输出结果如下
MeanAbsolute Error: 3.842909220444496
MeanSquared Error: 33.44897999767647
RootMean Squared Error: 5.78350931508513
总结
这节课中,我们使用了线性回归算法去实际处理了一个房价预测的问题,从数据的获取,数据的展示,再到模型训练和效果评估,算是一个比较完整的处理过程了。同时这节课里面也涉及了比较多的辅助代码,希望能够对你平时的工作或者学习有所帮助。
好了,这一节实践课就到此结束了,同时关于回归问题的讲解也告一段落。不知道你是否对这部分的内容有了一定的掌握。其实回归算法的理念很容易理解,只不过要找到适合你的数据的回归算法需要一些经验。
点击下方链接查看源代码(不定时更新)以及相关工具:
https://github.com/icegomic/GomicDatamining/tree/master/LagouCodes