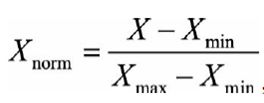小结:归一化Normalization(持续更新)
目录
- 0 归一化(N)
-
- 0.1 定义
- 0.2 标准化
- 0.3 中心化
- 特征缩放
-
- Rescalin /min-max scaling/min-max normalization/normalization
- Mean normalization
- Z-score normalization/Standardization
- Scaling to unit length
- 1 批归一化(BN)
-
- 1.1 提出背景
- 1.2 思路
- 1.3 算法步骤
- 1.3 可学习参数(γ,β)
- 1.4 公式
- 1.4 测试时怎么用?
- 1.5 BN的优势
- BN的用法
- 2 样本归一化(IN)
- 3 权重归一化(WN)
- 4 层归一化(LN)
- 5 组归一化(GN)
- 6 可选归一化(SN)
- 参考
0 归一化(N)
0.1 定义
目的:数据缩放,消除量纲,加快收敛,避免数值问题(太大,太小)
把数据变成 (0,1)或者(-1,1)之间 的小数
改变数据分布形状,变换后的数据有范围,可用于稳定数据
0.2 标准化
把数据的 不改变数据分布形状,均值变为0、标准差变为1 的数
在归一化范围内
改变数据分布形状,变换后的数据没有范围,可用于不稳定数据(多异常值,噪声)
0.3 中心化
把数据的 均值变为0,标准差无要求 的数
不在归一化范围内
不改变数据分布形状,变换后的数据没有范围
特征缩放
Rescalin /min-max scaling/min-max normalization/normalization
Mean normalization
Z-score normalization/Standardization
Scaling to unit length
1 批归一化(BN)
Batch Normalization
1.1 提出背景
2015,Google,Sergey Ioffe&Christian Szegedy
DNN难训练的原因:层与层间高度关联与耦合
本质原因:
(1)底层参数微弱变化,随层数加深,被放大
(2)参数变化,使每层输入分布变化,上层网络需要去适应(Internal Covariate Shift)
什么是内部协变量漂移? <\font>
内部协变量漂移(Internal Covariate Shift,ICS):由于网络中参数变化而引起内部结点数据分布发生变化的过程
每一层的线性变换:

每一层的非线性变换:
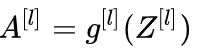
参数W,b被更新,Z分布变化,A分布变化
A是第l+1层的输入,意味着,第l+1层需要不断适应这种数据分布的变化
内部协变量漂移会带来什么问题? <\font>
(1)上层网络需要不断调整适应输入数据分布的变化,降低学习速率
(2)训练易陷入梯度饱和区,减缓收敛速度
W变大,Z变大,进入饱和区
问题(2)的解决思路:
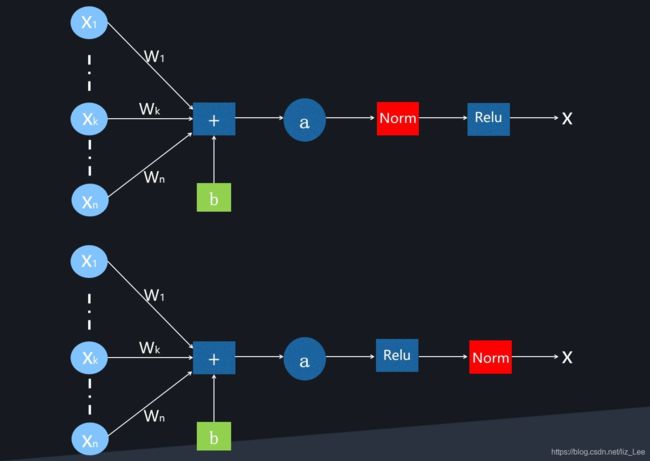
选用非饱和激活函数——》ReLU
让激活函数的分布保持在稳定状态——》Normalization
如何减缓内部协变量漂移? <\font>
(1)白化
对输入数据分布进行变换(PCA,ZCA),从而:
- 使输入特征分布有相同的均值和方差 (PCA是0,1;ZCA是0,常数)
- 去除特征间的相关性
白化的缺陷:
- 计算成本高
- 削弱了网络的数据表达能力
(2)BN
保持数据分布稳定
保留网络表达能力
1.2 思路
使每个特征的分布均值为0,方差为1(这个过程会削弱表达能力)
加一个线性变换,恢复网络的数据表达能力
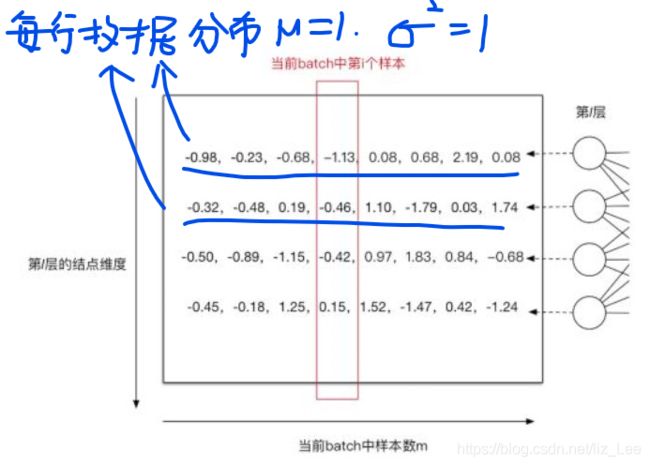
1.3 算法步骤
m:每批的样本数
j:当前层的第j个神经元

归一化前:

第一个神经元,求得:

归一化后:
1.3 可学习参数(γ,β)
非线性变换:保证网络的数据表达能力
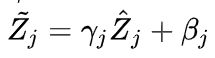
两个可学习参数:γ和β
当![]() 时,等价变换+保留原始输入特征的分布信息。
时,等价变换+保留原始输入特征的分布信息。
1.4 公式
1.4 测试时怎么用?
测试样本可能很少,μ和σ是有偏估计,怎么算?
用训练时每一批的μ_batch和σ_batch,对测试数据进行归一化
均值,方差的无偏估计:

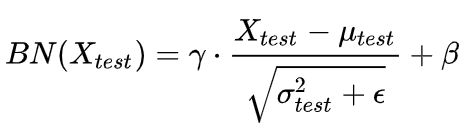
1.5 BN的优势
(1)使每层数据分布稳定,加速模型学习
上层网络不用去,不断适应底层网络输入的变化
(2)模型对网络参数不那么敏感,简化调参,网络学习更稳定
抑制了参数微小变化,随层数被放大的问题
初始化,学习率的微小变化,不会太过影响网络学习
(3)允许网络使用饱和激活函数,缓解其梯度消失问题
将激活函数输入约束在梯度非饱和区,又能用γ和β保留大量原始信息
底层网络变化累积到上层,进入梯度饱和区
(3)有一定正则化效果
用mini-batch的均值与方差,作为,对整体样本的均值与方差,的估计=增加了随机噪音
BN的用法
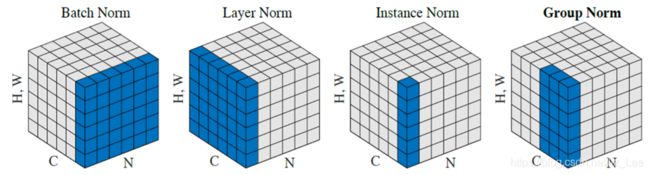
2 样本归一化(IN)
Instance Normalization
IN:在Pixel上,对HW做归一化
适用:风格化迁移
3 权重归一化(WN)
Weight Normalization
4 层归一化(LN)
Layer Normalization
在channel上,对C、H、W归一化
适用:RNN作用明显
5 组归一化(GN)
Group Normalization
将channel分组,然后再做归一化
6 可选归一化(SN)
Switchable Normalization
将BN、LN、IN结合,赋予权重,让网络学习归一化层。
参考
https://zhuanlan.zhihu.com/p/34879333
https://github.com/amusi/Deep-Learning-Interview-Book/blob/master/docs/%E6%B7%B1%E5%BA%A6%E5%AD%A6%E4%B9%A0.md#batch-normalizationbn
https://blog.csdn.net/liuxiao214/article/details/81037416
https://www.jianshu.com/p/95a8f035c86c
https://blog.csdn.net/hjimce/article/details/50866313
https://zhuanlan.zhihu.com/p/43200897
https://www.zhihu.com/question/20467170