PCA LDA 降维算法 介绍 实现 对比
PCA的原理、学习模型、算法步骤
PCA的目的是对于对于样本 x ∈ R d x\in \R^d x∈Rd,寻找到一个变换矩阵 W T , W ∈ R d × m , m < d W^T,W\in\R^{d\times m},m
从最大投影误差来解释PCA的原理,我们希望得到的 y y y在特征空间中能尽可能的分散,假设对于样本集合满足0均值化, ∑ x i = 0 \sum x_i=0 ∑xi=0,那么投影之后的新样本的协方差为: ∑ W T x i x i T W = W T X X T W \sum W^Tx_ix_i^TW=W^TXX^TW ∑WTxixiTW=WTXXTW,为了最大化协方差所以得到:
max W ∈ R d × m t r ( W T X X T W ) , s . t . W T W = I \max_{W\in \R^{d\times m}}tr(W^TXX^TW),\quad s.t.\ W^TW = I W∈Rd×mmaxtr(WTXXTW),s.t. WTW=I
求解上述优化问题可以得到只需要对协方差矩阵 X X T XX^T XXT进行特征分解,取前m个最大的特征值对应的特征向量构成变换矩阵即可。
算法步骤描述如下:
- 计算数据均值: x ˉ = 1 n ∑ i = 1 n x i \bar x = \frac 1n \sum_{i=1}^{n}x_i xˉ=n1∑i=1nxi
- 计算数据的协方差矩阵: C = 1 n ∑ i = 1 n ( x i − x ˉ ) ( x i − x ˉ ) T C = \frac1n\sum_{i=1}^{n}(x_i-\bar x)(x_i-\bar x)^T C=n1∑i=1n(xi−xˉ)(xi−xˉ)T
- 对矩阵 C C C进行特征值分解,并取最大的m个特征值( λ 1 ≥ λ 2 ≥ ⋯ ≥ λ m \lambda_1\ge\lambda_2\ge\cdots\ge\lambda_m λ1≥λ2≥⋯≥λm)对应的特征向量 w 1 , w 2 , ⋯ , w m w_1,w_2,\cdots,w_m w1,w2,⋯,wm,组成投影矩阵 W = [ w 1 , w 2 , ⋯ , w m ] ∈ R d × m W=[w_1,w_2,\cdots,w_m]\in\R^{d\times m} W=[w1,w2,⋯,wm]∈Rd×m
- 对每个数据样本进行投影 y i = W T x i ∈ R m y_i=W^Tx_i\in R^m yi=WTxi∈Rm
LDA的原理和学习模型
LDA的目的也是对于对于样本 x ∈ R d x\in \R^d x∈Rd,寻找到一个变换矩阵 W T , W ∈ R d × m , m < d W^T,W\in\R^{d\times m},m
记 μ = 1 n ∑ x i \mu=\frac1n\sum x_i μ=n1∑xi为所有样本的平均,定义全局的散度矩阵 S t = ∑ ( x i − μ ) ( x i − μ ) T S_t=\sum(x_i-\mu)(x_i-\mu)^T St=∑(xi−μ)(xi−μ)T。定义 S w j S_{wj} Swj为第j类样本的类内散度矩阵 S w j = ∑ x ∈ X j ( x − μ j ) ( x − μ j ) T , μ j = 1 n j ∑ x ∈ X j x S_{wj}=\sum_{x\in X_j}(x-\mu_j)(x-\mu_j)^T,\mu_j=\frac{1}{n_j}\sum_{x\in X_j}x Swj=∑x∈Xj(x−μj)(x−μj)T,μj=nj1∑x∈Xjx。(总)类内散度矩阵为所有类别的类内的和 S w = ∑ j = 1 c S w j S_w=\sum_{j=1}^c S_{wj} Sw=∑j=1cSwj,定义类间散度矩阵为 S b = ∑ j = 1 c n j ( μ j − μ ) ( μ j − μ ) T S_b=\sum_{j=1}^c n_j(\mu_j-\mu)(\mu_j-\mu)^T Sb=∑j=1cnj(μj−μ)(μj−μ)T,事实上也可以通过 S b = S t − S w S_b=S_t-S_w Sb=St−Sw来计算。
依据LDA的目的,需要最大化
max t r ( W T S b W ) t r ( W T S w W ) s . t . W T W = I o r max ∣ W T S b W ∣ ∣ W T S w W ∣ s . t . W T W = I \max \frac{tr(W^TS_bW)}{tr(W^TS_wW)}\quad s.t.\ W^TW = I\\ or\\ \max \frac{|W^TS_bW|}{|W^TS_wW|}\quad s.t.\ W^TW = I\\ maxtr(WTSwW)tr(WTSbW)s.t. WTW=Iormax∣WTSwW∣∣WTSbW∣s.t. WTW=I
当选用后者使用行列式的值比为优化目标时,可以通过求解如下广义特征值问题得到:
S b w = λ S w w S_b w=\lambda S_w w Sbw=λSww
将求解得到的最大的m个特征值对应的特征向量拼接起来,即可得到需要求解的 W W W。
使用PCA 和 LDA 进行实战
使用数据集AT&T
数据集为人脸数据集,包含多张人脸图像,任务是按照人进行分类。随机抽出一张图片可视化如下:
使用PCA降维度和LDA降维对图像进行降维,降维后采用1近邻KNN进行分类,测试集分类正确率随降低到不同维数时的变化如下:
(LDA算法在计算特征值时至多得到 类 别 数 − 1 类别数-1 类别数−1 个非0的特征向量,因此也最多通过选择非0特征值对应的 类 别 数 − 1 类别数-1 类别数−1 个特征向量得到 类 别 数 − 1 类别数-1 类别数−1 维的降维表示,红色区域表示的LDA算法计算得到的超过 类 别 数 − 1 类别数-1 类别数−1 的降维效果,可以理解为在 类 别 数 − 1 类别数-1 类别数−1 的基础上添加了随机的额外投影方向)

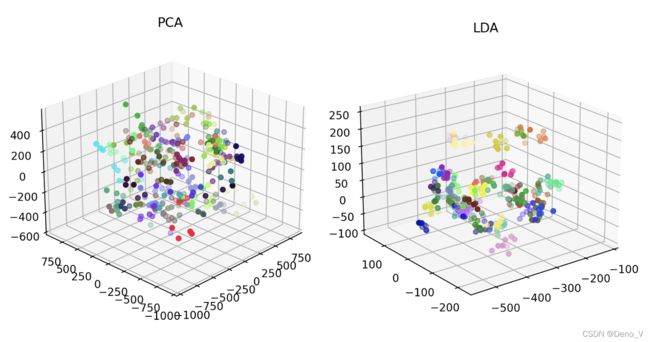
在AT&T数据集上,使用PCA和LDA将数据降低到三维,可视化二者如下:
可以看到PCA和LDA的降维效果是有显著差别的,LDA能将不同类别的样本区别的更明显。
使用数据集Vehicle
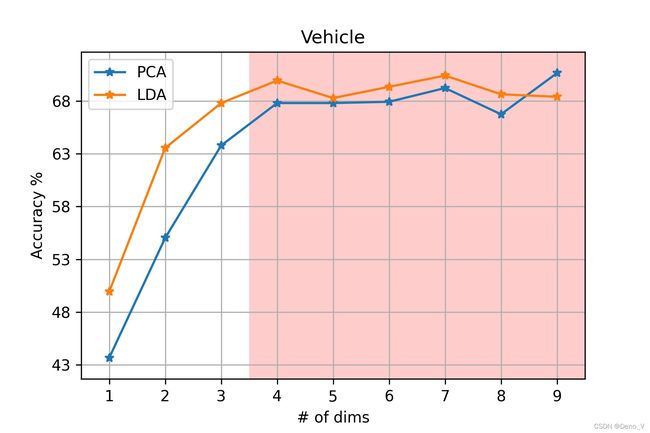
使用PCA降维度和LDA降维对图像进行降维,降维后采用1近邻KNN进行分类,测试集分类正确率随降低到不同维数时的变化如下:
(LDA算法在计算特征值时至多得到 类 别 数 − 1 类别数-1 类别数−1 个非0的特征向量,因此也最多通过选择非0特征值对应的 类 别 数 − 1 类别数-1 类别数−1 个特征向量得到 类 别 数 − 1 类别数-1 类别数−1 维的降维表示,红色区域表示的LDA算法计算得到的超过 类 别 数 − 1 类别数-1 类别数−1 的降维效果,可以理解为在 类 别 数 − 1 类别数-1 类别数−1 的基础上添加了随机的额外投影方向)
评价
对于两个数据集来说LDA和PCA都没有显著差异,在AT&T上PCA表现略优于LDA方法。
核心代码
数据集自己查找或私信
from matplotlib import pyplot as plt
import numpy as np
from scipy import io
from collections import Counter as count
import random
# 1阶knn
class knn_1:
def __init__(self,x,y):
# x: nxd, ndarray
# y: n, ndarray
self.y = y
self.xmean = np.mean(x,axis=0)
self.xstd = np.std(x,axis=0)
self.x = self.prepare(x)
def prepare(self,x):
# uniform data
return (x-self.xmean)/self.xstd
def __call__(self,z):
# z: nxd, ndarray
z = self.prepare(z.reshape(-1,z.shape[1]))
out = []
for vz in z:
diff = np.abs(self.x - vz)
diff = diff**2
diff = np.sum(diff,axis=1)
out.append(self.y[np.argmin(diff)])
return np.array(out)
# pca
class pca:
def __init__(self,x,d):
#d: num of dims after lda
# x: nxd, ndarray
# y: n, ndarray
assert(d<x.shape[1])
mean = np.mean(x,axis=0)
x_ = x - mean
cov = np.cov(x_,rowvar=0)
eigVals,eigVects = np.linalg.eig(cov)
eigValIndice = np.argsort(eigVals)
n_eigValIndice = eigValIndice[-1:-(d+1):-1]
n_eigVect = eigVects[:,n_eigValIndice]
self.W = n_eigVect
self.mean = mean
def __call__(self,z):
# z: nxd, ndarray
z = z.reshape(-1,z.shape[1])
return (z-self.mean)@self.W
# lda
class lda:
def __init__(self,x,y,d):
#d: num of dims after lda
# x: nxd, ndarray
# y: n, ndarray
assert(d<x.shape[1])
mean = np.mean(x,axis=0)
x_ = x - mean
st = x_.T@x_
sw = np.zeros([x.shape[1]]*2)
distribute_y = count(y)
for i in distribute_y.keys():
pickindex = (y==i)
pickx = x[pickindex]
pickmean = np.mean(pickx,axis=0)
pickx_ = pickx - pickmean
sw += pickx_.T@pickx_
sb = st - sw
eigVals,eigVects = np.linalg.eig(np.linalg.pinv(sw)@sb)
eigValIndice = np.argsort(eigVals)
n_eigValIndice = eigValIndice[-1:-(d+1):-1]
n_eigVect = eigVects[:,n_eigValIndice]
self.W = n_eigVect
self.sw = sw
self.sb = sb
def __call__(self,z):
# z: nxd, ndarray
z = z.reshape(-1,z.shape[1])
return z@self.W
# 分层采样划分测试集和训练集
from random import sample
def split(x,y,ratio):
# ration in [0,1] decides the ratio of training data
# 分层采样
x_train = []
x_test = []
y_train = []
y_test = []
distribute_y = count(y)
for i in distribute_y.keys():
total = distribute_y[i]
trainnum = round(ratio*total)
testnum = total - trainnum
pickx = x[y==i]
allindex = list(range(pickx.shape[0]))
trainindex = sample(allindex,trainnum)
testindex = list(set(allindex)-set(trainindex))
x_train.append(pickx[trainindex].reshape(trainnum,-1))
x_test.append(pickx[testindex].reshape(testnum,-1))
y_train.append([i]*trainnum)
y_test.append([i]*testnum)
x_train = np.concatenate(x_train,axis=0)
x_test = np.concatenate(x_test,axis=0)
y_train = np.concatenate(y_train)
y_test = np.concatenate(y_test)
return x_train,x_test,y_train,y_test
#读如第一个数据集
data = io.loadmat('ORLData_25.mat')['ORLData'].T
X = data[:,:-1]
Y = data[:,-1]
print(data.shape,data.dtype)
print(X.shape,X.dtype)
print(Y.shape,Y.dtype)
plt.imshow(X[0].reshape(23,28).T,cmap='gray')
plt.savefig('face.jpg',dpi=100)
# 读如第二个数据集
#data = io.loadmat('vehicle.mat')['UCI_entropy_data'][0][0][4].T
#X = data[:,:-1]
#Y = data[:,-1]
#print(data.shape,data.dtype)
#print(X.shape,X.dtype)
#print(Y.shape,Y.dtype)
#LDA
K = 8
d = 10
acc_list = []
for _ in range(K):
x_train,x_test,y_train,y_test = split(X,Y,0.8)
ldamodel = lda(x_train,y_train,d)
trainx = ldamodel(x_train)
testx = ldamodel(x_test)
knnmodel = knn_1(trainx,y_train)
pred = knnmodel(testx)
acc_list.append(np.sum(pred==y_test)/y_test.shape[0])
print(acc_list)
#PCA
K = 8
d = 10
acc_list = []
for _ in range(K):
x_train,x_test,y_train,y_test = split(X,Y,0.8)
pcamodel = pca(x_train,y_train,d)
trainx = pcamodel(x_train)
testx = pcamodel(x_test)
knnmodel = knn_1(trainx,y_train)
pred = knnmodel(testx)
acc_list.append(np.sum(pred==y_test)/y_test.shape[0])
print(acc_list)
#combined
K = 5
dlist = list(range(2,60,5))
pca_list = []
for d in dlist:
acc_klist = []
for _ in range(K):
x_train,x_test,y_train,y_test = split(X,Y,0.8)
pcamodel = pca(x_train,d)
trainx = pcamodel(x_train)
testx = pcamodel(x_test)
knnmodel = knn_1(trainx,y_train)
pred = knnmodel(testx)
acc_klist.append(np.sum(pred==y_test)/y_test.shape[0]*100)
pca_list.append(np.array(acc_klist).mean())
lda_list = []
for d in dlist:
acc_klist = []
for _ in range(K):
x_train,x_test,y_train,y_test = split(X,Y,0.8)
ldamodel = lda(x_train,y_train,d)
trainx = ldamodel(x_train)
testx = ldamodel(x_test)
knnmodel = knn_1(trainx,y_train)
pred = knnmodel(testx)
acc_klist.append(np.sum(pred==y_test)/y_test.shape[0]*100)
lda_list.append(np.array(acc_klist).mean())
plt.plot(dlist,pca_list,'-*',label='PCA')
plt.plot(dlist,lda_list,'-*',label='LDA')
plt.grid()
plt.legend()
plt.xlabel('# of dims')
plt.ylabel('Accuracy %')
plt.title('Vehicle')
plt.xlim([dlist[0]-1,dlist[-1]+1])
plt.xticks(dlist)
plt.yticks(range(round(min(pca_list+lda_list))-1,round(max(pca_list+lda_list))+1,5))
plt.axis([min(dlist)-0.5,max(dlist)+0.5,min(pca_list+lda_list)-2,max(pca_list+lda_list)+2])
plt.fill_between([39.5,max(dlist)+1],[0,0],[100,100],facecolor='red',alpha=0.2)
plt.savefig('AT&T.jpg',dpi=300)