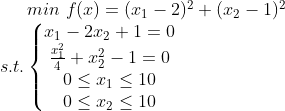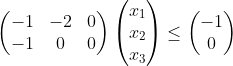MATLAB遗传算法工具箱的使用及实例(非线性规划)

本文将介绍MATLAB遗传算法工具箱求解非线性规划问题。在阅读本文之前，建议读者阅读上一期“MATLAB遗传算法工具箱求解线性规划问题”。文章传送门：https://blog.csdn.net/weixin_45012973/article/details/107282323

一、引例

上一期介绍了遗传算法求解线性规划的问题。我们来看看下面这个例子，能否用上次讲的方法解决。

上述例子，第二个约束条件含有二次项，并不是线性的，用上次的方法好像无法直接解决。下面我们就来介绍一下非线性规划的遗传算法的实现。

二、非线性规划的标准形式

2.1 非线性规划的标准形式

和线性规划一样，在调用遗传算法工具箱之前，也得学习一下非线性规划的标准形式。因为，调用工具箱需要我们将非标准形式的模型转化为标准形式。

其中，是目标函数，线性或者非线性都可以。式[1]、式[2]、式[5]同线性规划，为相应维数的矩阵和向量。式[3]表示非线性的不等式约束，式[4]是非线性等式约束。和为非线性向量函数（这里可能不好理解，下面结合一个例子解释）

2.2 非线性规划的例子

例如以下模型

可以看出，这个模型没有线性约束，式[1]、式[2]、式[3]、式[4]均为非线性的。其中，式[1]、式[2]是非线性不等式约束，式[3]、式[4]是等式约束。对于非标准的非线性规划模型，我们先得化为标准的模型，转化方式和线性规划相同，采用添负号或者乘-1的方式。

1) 将不等式约束(式[1]、[2])转化为  的形式（注意，小于号右边为0，常数需移到左边，这是和线性约束不一样的地方）

注意到这里的  应是一个向量函数，本模型中有两个不等式约束，函数  的返回值应该是两个数。（看不懂没关系，编程时会具体讲解如何编写）

2) 将等式约束(式[3]、[4])转化为的形式（注意，等号右边为0，常数需要移到左边，这是和线性约束不一样的地方）

注意到这里的  应是一个向量函数，本模型中有两个等式约束，函数  的返回值应该式是两个数。（看不懂没关系，编程时会具体讲解如何编写）

三、使用遗传算法工具箱对模型进行求解

MATLAB提供的遗传算法工具箱，主要分为两个函数：gaoptimset()函数和ga()函数，gaoptimset()函数是用于设置遗传算法的一些参数的，可以不设置。若不设置，就使用默认参数。ga()函数是调用遗传算法对优化问题进行计算。

3.1 设置遗传算法的一些参数——gaoptimset()函数的使用

调用格式为: options = gaoptimset('Param1', value1, 'Param2', value2, ...);

 其中，'Param1'、'Param2'等是需要设定的参数，比如：种群规模、交叉比例等。value1、value2等则是Param的具体值。常用的参数名如下表（只列出了常用的，还有很多参数可以调整，可自行上网搜索）：

gaoptimset函数的常用选项

设定的参数名(Param名)	说明	默认值
CrossoverFraction	交叉比例	0.8
Generations	算法中止的最大迭代次数	100
PopulationSize	种群规模	20
MigrationFraction	变异概率	0.2
FitnessLimit	当适应度函数达到设定的值时算法中止	-
StallGenLimit	当超过StallGenLimit代适应度函数为改善时，算法中止	50

例如，需要设置交叉比例为0.7、迭代次数为300、种群规模为30，代码写作

options = gaoptimset('CrossoverFraction', 0.7, 'Generations', 300, 'PopulationSize', 30);

返回的options是结构体，用于ga函数的最后一个参数

3.2  开始遗传算法的计算——ga()函数的使用

ga函数的调用格式为：

[x_best,fval] = ga(fun, nvars, A, b, Aeq, beq, lb, ub, nonlcon, options);

参数名	fun	nvars	A	b	Aeq	beq	lb	ub	nonlcon	options
含义	目标函数句柄	自变量个数	线性不等式约束 (以矩阵形式表示，下同)		线性等式约束		自变量的定义域		非线性约束函数句柄	上一步gaoptimset函数返回的结构体
备注	如果某个参数不需要，就设置为空矩阵[]

返回值x_best为取到最小值时的自变量x的取值，fval为所求的最小值。

四、非线性规划模型的实例

4.1 还是前面出现的模型

      

1) 编写适应度函数(即目标函数)

目标函数的编写就不多说了，和之前线性规划的编写方法相同

function f = fitnessfun(x)
    f = x(1)^2 + x(2)^2 + x(3)^3 + 8;
end

2) 编写非线性约束函数

根据式[1]、[2]，非线性不等式约束的函数为： ，

根据式[3]、[4]，等式约束的函数为： 

非线性约束函数和需要在MATLAB中编写为如下格式（写在一个function里）

function [c, ceq] = 函数名(x)

参数和返回值解释：

x即为自变量的值，为行向量。c即不等式约束的函数值，是列向量（可以存在多个约束）。ceq即等式约束函数的函数值，同样是列向量（可以存在多个约束）

也就是本题返回值要写成这样的形式（这样看的更直观一些）：

因此，这题的function应定义为

function [c,ceq] = nonlconfun(x)
    % 入口参数 x:为自变量的行向量
    % 出口参数 c:非线性不等式约束的函数值。由于本题有两个不等式约束
    %           因此c(1,1)为第一个不等式约束函数值，c(2,1)为第二个不等式约束函数值
    %        ceq:非线性等式约束的函数值，由于本题有两个等式约束，同c一样
    %            ceq(1,1)为第一个等式约束函数值，ceq(2,1)为第二个等式约束函数值
    c(1,1) = -x(1)^2 + x(2) - x(3)^3;
    c(2,1) = x(1) + x(2)^2 + x(3)^3 - 20;
    ceq(1,1) = -x(1) - x(2)^2 + 2;
    ceq(2,1) = x(2) + 2*x(3)^2 - 3;
end

3) 设置遗传算法工具箱的相关参数

（如不知道相关参数如何配置，可参见上一期遗传算法工具箱求解线性规划的博客）

这里我们设置种群规模300，迭代次数为800，返回值为options.

options = gaoptimset('PopulationSize', 300, 'Generations', 800);

4) 调用ga工具箱

我们知道，ga工具箱的调用格式为：

[x_best,fval] = ga(fun, nvars, A, b, Aeq, beq, lb, ub, nonlcon, options);

由于本题没有线性约束，因此参数A、b、Aeq、beq都可以设置为空。

对自变量x的约束为：，因此，，而ub可以不设置

因此，这部分代码为

options = gaoptimset('PopulationSize', 300, 'Generations', 800); % 遗传算法相关配置
fun = @fitnessfun; % 设置适应度函数句柄
nonlcon = @nonlconfun; % 设置非线性约束函数句柄
nvars = 3; % 自变量个数
A = [];  b = [];
Aeq = [];  beq = [];
lb = [0;0;0];  ub = [];
[x_best, fval] = ga(fun, nvars, A, b, Aeq, beq, lb, ub, nonlcon, options);

完整的代码为：

clear;
clc
options = gaoptimset('PopulationSize',200, 'Generations', 600); % 遗传算法相关配置
fun = @fitnessfun; % 设置适应度函数句柄
nonlcon = @nonlconfun; % 设置非线性约束函数句柄
nvars = 3; % 自变量个数
A = [];  b = [];
Aeq = [];  beq = [];
lb = [0;0;0];  ub = [];
[x_best, fval] = ga(fun, nvars, A,b,Aeq,beq,lb,ub,nonlcon,options);

function [c,ceq] = nonlconfun(x)
    c(1,1) = -x(1)^2 + x(2) - x(3)^3;
    c(2,1) = x(1) + x(2)^2 + x(3)^3 - 20;
    ceq(1,1) = -x(1) - x(2)^2 + 2;
    ceq(2,1) = x(2) + 2*x(3)^2 - 3;
end

function f = fitnessfun(x)
    f = x(1)^2 + x(2)^2 + x(3)^3 + 8;
end

运行结果为

fval的值为10.9886即为所求，此时x_best的值为[0.9917    1.0041    0.9988].

因此当时，函数取到最小值10.9886

（遗传算法具有一定随机性，每次的运行结果有差别，建议多运行几遍程序，找一个最好的结果）

4.2 求下列问题的解

1) 编写目标函数

function f = fitnessfun(x)
    f = -2 * x(1) - 3 * x(1)^2 - 3 * x(2) - x(2)^2 - x(3);
end

2）编写非线性约束函数

式[1]、[2]、[3]为非线性不等式约束，式[4]为非线性等式约束，因此

，  

使用MATLAB编写为：

function [c,ceq] = nonlconfun(x)
    % 入口参数 x:为自变量的行向量
    % 出口参数 c:非线性不等式约束的函数值。由于本题有多个不等式约束，以列向量的形式返回即可
    %         ceq:非线性等式约束的函数值。
    c(1,1) = x(1) + 2 * x(1)^2 + x(2) + 2 * x(2)^2 + x(3) - 10;
    c(2,1) = x(1) + x(1)^2 + x(2) + x(2)^2 - x(3) - 50;
    c(3,1) = 2 * x(1) + x(1)^2 + 2 * x(2) + x(3) - 40;
    ceq = x(1)^2 + x(3) - 2;
end

3）调用ga函数

（这里就不调用gaoptimset函数配置遗传算法的参数了，直接使用默认参数）

式[5]、[6]为线性不等式约束，标准形式为

 可转化为： ，因此：

本题没有线性等式约束，也没有自变量约束，因此Aeq、beq、lb、ub均设置为空矩阵。写好ga所需的入口参数，即可调用ga函数，调用方式如下：

fun = @fitnessfun; % 设置适应度函数句柄，(在函数名前加@即可)
nonlcon = @nonlconfun; % 设置非线性约束函数句柄
nvars = 3; % 自变量个数
A = [-1,-2,0;-1,0,0];  b = [-1;0];  % 线性不等式约束
Aeq = [];  beq = []; % 线性等式约束
lb = [];  ub = [];   % 自变量定义域
[x_best, fval] = ga(fun, nvars, A, b, Aeq, beq, lb, ub, nonlcon, []);

整体程序为：

clear;
clc
fun = @fitnessfun; % 设置适应度函数句柄，(在函数名前加@即可)
nonlcon = @nonlconfun; % 设置非线性约束函数句柄
nvars = 3; % 自变量个数
A = [-1,-2,0;-1,0,0];  b = [-1;0];  % 线性不等式约束
Aeq = [];  beq = [];   % 线性等式约束
lb = [];  ub = [];     % 自变量定义域
[x_best, fval] = ga(fun, nvars, A,b,Aeq,beq,lb,ub,nonlcon,[]);

function [c,ceq] = nonlconfun(x)
    c(1,1) = x(1) + 2 * x(1)^2 + x(2) + 2 * x(2)^2 + x(3) - 10;
    c(2,1) = x(1) + x(1)^2 + x(2) + x(2)^2 - x(3) - 50;
    c(3,1) = 2 * x(1) + x(1)^2 + 2 * x(2) + x(3) - 40;
    ceq = x(1)^2 + x(3) - 2;
end

function f = fitnessfun(x)
    f = -2 * x(1) - 3 * x(1)^2 - 3 * x(2) - x(2)^2 - x(3);
end

运行程序后，得到运行结果：fval的值为 -15.2409.由于我们在标准化模型时，将目标函数添加了一个负号，因此原函数的最大值约为15.2409.

（遗传算法具有一定随机性，每次的运行结果有差别，建议多运行几遍程序，找一个最好的结果）

遗传算法工具箱求解非线性规划的内容就介绍到这里，看完这些，相信你也能解决文章开始的引例了！