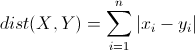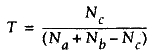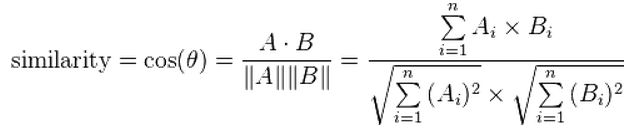马氏距离 java实现_相似度计算方式的总结：java或python实现代码 | 学步园

缘由

这是之前定了的方案：

我想要对比由不同相似度计算出来的歌曲相似度表，

再由不同的歌曲相似度表来产生推荐列表，

比较推荐列表中出现的我随机删除了的本来就被用户收藏了的歌曲的数量

肯定有一种相似度计算公式最优

根据原理分析为什么这种相似度方案最优

即可产生理论，有了论据

所以，现在我目标是总结常见的几种相似度计算方式的原理，并且利用mahout找到其实现的源代码，能够利用源代码做一些简答的实验。

我的这篇博客很大程序上参考了下面一篇优秀的博客，感谢原作者：

导入mahout源码

下载源码，下载文件：mahout-distribution-0.9-src.zip(上传至网盘)

导入源码，由于不是一般的文件，所以必须使用maven，流程参考Eclipse 安装SVN、Maven插件。下载maven又需要安装Marketplace Client，方式请见：在eclipse上安装

Marketplace Client

接着展开相应的目录，就可以看到源码。如下图所示：

除了上面这个目录以外，别的目录还有一些距离计算代码，如下图所示：

我并非像直接调用mahout提供给我们的api，而且参考其代码的书写方式，自己写相应的代码。之前说过python计算速度太慢，我也考虑了实际使用java来计算一下歌曲的相似度。

欧几里得距离

英文名为：Euclidean distance，又称欧式距离。在读书笔记：“集体智慧编程”之第二章：推荐算法中，我已经学习过了，主要方式就是考虑点与点之间的距离，无论是几维的，但是我们可以两维的情况来估计N多维的情况。主要使用的公式如下(来自wiki)：

注意等号后面的Xi代表的是等号前面的大X的某一个分量。当n=2时，就代表是2维的。也就是说大X和大Y只有两个分量。

当我们使用欧几里得距离来计算相似度的时候，如果两者完全相似的话，那么两点重合，所以距离为0。如果两者距离很远的话，那么数值会很大，代表着两者非常不相似。然而，一般在使用中，我们都希望用[0,1]来表示相似度，而完全相似度的情况用1来表示，所以，我们通常会将dist(X,Y)结果取倒数。如此一来，当两者完全重合时为0，所以我们会加对分母加1，防止这样的情况，所以最后应该为：

1/(1+dist(X,Y))

java代码：

下段代码来自mahout的org.apache.mahout.cf.taste.impl.similarity.EuclideanDistanceSimilarity：

double computeResult(int n, double sumXY, double sumX2, double sumY2, double sumXYdiff2) {

return 1.0 / (1.0 + Math.sqrt(sumXYdiff2) / Math.sqrt(n));

}

其中传入参数的含义如下，来自：org.apache.mahout.cf.taste.impl.similarity.AbstractSimilarity

sumXY += x * y;//x,y代表两个向量中的每一对分量

sumX += x;

sumX2 += x * x;

sumY += y;

sumY2 += y * y;

double diff = x - y;

sumXYdiff2 += diff * diff;

很容易理解其代码，唯一让我感到疑惑就是mahout在使用这个计算方式的时候还除以了n的开方：

1.0 / (1.0 + Math.sqrt(sumXYdiff2) / Math.sqrt(n));

具体有什么好处呢，暂时说不上来，也许我在实际应该用中会发现。

优点：

简单

缺点：

未考虑分量之间的关系

如果分量的单位不同，比如对身高(cm)和体重(kg)两个单位，那么必须先对各分量进行标准化，使其与单位无关。为了理解这样的说法，请极端考虑，当一个分量的变化范围在0到1000之间，然而另一份分量的变化范围就是0或者1(也就是：是与否的数值化表示)。很显然0到1000的这个分量会对结果产生极大的影响。这属于对数据进行缩放的问题。在读书笔记：“集体智慧编程”之第九章：高阶分类-核方法与SVM中提到过。

马氏距离

即：Mahalanobis distance。该距离较为复杂，从wiki百科来看，其表示：数据的协方差距离

公式为：

优点：

考虑到各种特性之间的联系(例如：一条关于身高的信息会带来一条关于体重的信息，因为两者是有关联的)

独立于测量尺度：即为尺度无关。

缺点：

不同的特征不能差别对待，可能夸大弱特征。(摘自博客，我是不太懂其意思)

python代码

曼哈顿距离

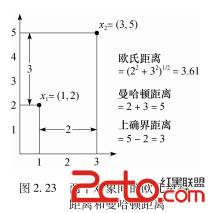
即Manhattan Distance，与欧几里得距离对比起来，比较好理解。如下图所示(摘自wiki)：

上图中的红、黄、蓝线的长度其实是相等的，这个距离就是曼哈顿距离，其中绿线就是欧几里得距离。亦可从数值上来直观的看(摘自2cto)：

在多维空间中的公式如下，多维空间中依然有效：

java代码

摘自org.apache.mahout.common.distance.ManhattanDistanceMeasure：

public static double distance(double[] p1, double[] p2) {

double result = 0.0;

for (int i = 0; i < p1.length; i++) {

result += Math.abs(p2[i] - p1[i]);

}

return result;

}

扩展公式

曼哈顿距离有两个扩展公式：闵可夫斯基距离和切比雪夫距离，其对应于mahout中的类：MinkowskiDistanceMeasure和ChebyshevDistanceMeasure，也就是说mahout对两个距离均有实现。

闵可夫斯基距离公式如下：

公式中p大于1。

切比雪夫距离公式如下：

公式中的q=∞时。

汉明距离

抓住两个关键点理解这个距离：

两个等长的字符串比较

字符串对应位置的不一样的字符的个数

比如：

1 与 0 之间的汉明距离是 1。

214 与 214 之间的汉明距离是 0。

"abcd" 与 "aacd" 之间的汉明距离是 1。

Tanimoto系数

也称广义Jaccard系数，在博客 读书笔记：“集体智慧编程”之第二章：推荐算法 已经介绍过了，举例说明：如有两个集合

A=[shirt,shoes,pants,socks]

B=[shirt,shirt,shoes]

两个集合的交集，就是重叠部分，我们称之为C。就是[shirt,shoes]。

Na表示集合A的个数，Nb表示集合B的个数。Nc表示集合C的个数。

Tanimote系数公式如下：

即Nc=2、Na=4、Nb=3，故T=2/(4+3-2)=0.4

python代码

def Jaccard(a,b):

c=[v for v in a if v in b]

return float(len(c))/(len(a)+len(b)-len(c))

另一说法：

上述说法主要来自：集体智慧编程一书

博客距离和相似度度量，提出了另一说法，公式如下：

并且做了解释了公式的含义：

我认为也不无道理。wiki也对此有着完整的论述。同时，mahout的java实现代码也采用了这样的方式：

java代码

来自：org.apache.mahout.common.distance.TanimotoDistanceMeasure

/**

* Calculates the distance between two vectors.

*

* The coefficient (a measure of similarity) is: T(a, b) = a.b / (|a|^2 + |b|^2 - a.b)

*

* The distance d(a,b) = 1 - T(a,b)

*

* @return 0 for perfect match, > 0 for greater distance

*/

@Override

public double distance(Vector a, Vector b) {

double ab;

double denominator;

if (getWeights() != null) {

ab = a.times(b).aggregate(getWeights(), Functions.PLUS, Functions.MULT);

denominator = a.aggregate(getWeights(), Functions.PLUS, Functions.MULT_SQUARE_LEFT)

+ b.aggregate(getWeights(), Functions.PLUS, Functions.MULT_SQUARE_LEFT)

- ab;

} else {

ab = b.dot(a); // b is SequentialAccess

denominator = a.getLengthSquared() + b.getLengthSquared() - ab;

}

if (denominator < ab) { // correct for fp round-off: distance >= 0

denominator = ab;

}

if (denominator > 0) {

// denominator == 0 only when dot(a,a) == dot(b,b) == dot(a,b) == 0

return 1.0 - ab / denominator;

} else {

return 0.0;

}

}

Jaccard系数

与Tanimoto有类似的地方，其公式如下：

可以看出，其含义是集合A、B中相同的个数，除以A与B交集个数。可以看出，Jaccard系统主要关注的是元素是的个体是否相同，而不能用数值具体表示其差异。从这个意义上讲，我认为适合我的音乐，音乐推荐中计算相似度的过程。因为，我确定两个用户是否相似就是判断这两个用户是否收藏了相同的歌曲。

举例：

A=[shirt,shoes,pants,socks]

B=[shirt,shirt,shoes]

个人认为，这里我们是将其作为集合来看的话，由于集合的互异性，所以B改为：B=[shirt,shoes]

交集：2

并集：4

Jaccard系数为2/4=0.5

python代码

与Tanimoto的代码类似，但是必须对每一个集合使用一次去重，实现集合的互异性

def Jaccard(a,b):

c=[v for v in a if v in b]

return float(len(c))/(len(a)+len(b)-len(c))

皮尔逊相关系数

由于在我的博客：读书笔记：“集体智慧编程”之第二章：推荐算法 有详细的介绍，也有python代码，这里就不赘述了。

余弦相似度

简单说来：余弦相似度两个向量之间的夹角的余弦值，无论在多少维的空间中都能有这个夹角。

推导公式(wiki)如下：

欧几里得点积和量级公式：

进而有：

其中||a||表示向量的模

可以看出其值是-1到1之间，当大于90度之后，就成为了负数。完全相似时为1,0表示彼此相互独立，而负数表示负相关。

java代码

代码摘自mahout的org.apache.mahout.common.distance.CosineDistanceMeasure类，给了三种实现方式，我暂时只贴两种我看得懂的，我认为难度不大：

public static double distance(double[] p1, double[] p2) {

double dotProduct = 0.0;

double lengthSquaredp1 = 0.0;

double lengthSquaredp2 = 0.0;

for (int i = 0; i < p1.length; i++) {

lengthSquaredp1 += p1[i] * p1[i];

lengthSquaredp2 += p2[i] * p2[i];

dotProduct += p1[i] * p2[i];

}

double denominator = Math.sqrt(lengthSquaredp1) * Math.sqrt(lengthSquaredp2);

// correct for floating-point rounding errors

if (denominator < dotProduct) {

denominator = dotProduct;

}

// correct for zero-vector corner case

if (denominator == 0 && dotProduct == 0) {

return 0;

}

return 1.0 - dotProduct / denominator;

}

@Override

public double distance(Vector v1, Vector v2) {

if (v1.size() != v2.size()) {

throw new CardinalityException(v1.size(), v2.size());

}

double lengthSquaredv1 = v1.getLengthSquared();

double lengthSquaredv2 = v2.getLengthSquared();

double dotProduct = v2.dot(v1);

double denominator = Math.sqrt(lengthSquaredv1) * Math.sqrt(lengthSquaredv2);

// correct for floating-point rounding errors

if (denominator < dotProduct) {

denominator = dotProduct;

}

// correct for zero-vector corner case

if (denominator == 0 && dotProduct == 0) {

return 0;

}

return 1.0 - dotProduct / denominator;

}

其他总结

优秀博客

解析数据挖掘的角色

数据的游戏：冰与火，这篇博客非常优秀，需要我单独列出来说明，我认为多读几遍非常好。下面几句话摘自该博客，我认为对我应聘有启示：

最没技术含量的是Software Developer：而像什么K-Means，K Nearest Neighbor，或是别的什么贝叶斯、回归、决策树、随机森林等这些玩法，都很成熟了，而且又不是人工智能，说白了，这些算法在机器学习和数据挖掘中，似乎就像Quick Sort之类的算法在软件设计中基本没什么技术含量。当然，我不是说算法不重要，我只想说这些算法在整个数据处理中是最不重要的。

最苦逼，也最累，但也最重要的是Data Analyzer：他们的活也是这三个角色中最最最重要的(注意：我用了三个最)。因为，无论你的模型你的算法再怎么牛，在一堆烂数据上也只能干出一堆垃圾的活来。正所谓：Garbage In, Garbage Out ！但是这个活是最脏最累的活，也是让人最容易退缩的活。

应聘的启示：

像一些基本的算法：K-Means，K Nearest Neighbor，或是别的什么贝叶斯、回归、决策树、随机森林，我必须烂熟于心。

我应该强调我如何利用这些算法自己构建了音乐推荐系统，怎么寻找、利用了网上已有的数据，怎么从无到有的产生了中文歌曲的推荐系统。这样显得自己实际应用能力更强。

项目相关

我不想盲目的使用所有的相似度计算方式来计算歌曲的相似度列表。我想使用其中一个我认为比较有意义：

Jaccard系数：这是因为我主要是根据两个用户收藏的歌曲来计算其相似度的，对于某一个首歌曲，如果A用户收藏了，其值为1，没有收藏，其值为0。