论文阅读：Rethinking the Inception Architecture for Computer Vision

论文阅读：Rethinking the Inception Architecture for Computer Vision

这篇论文是Inception 结构的一次改进，作者Christian Szegedy基于Inception提出了进一步提升卷积网络性能的几点原则，并结合实验对所提出的几点原则进行论证，进而提出了Inception-v2以及Inception-v3。

摘要

作者提到虽然扩大模型，增加计算能力可以在数据集充分的情况下提升卷积网络模型的性能，但是对于移动端的视觉任务以及大数据的任务场景来说，降低参数数量、提高计算效率依然是值得探讨的因素。

作这在这篇文章中探讨了通过因子卷积（Factorized Convlution)以及进一步的正则化（aggressive regularization)来保证增加的算力的计算效率，从而进一步括大模型的方法。

作者基于上诉方法进行对比实验，选择ILSVRC2012 classification作为benchmark,获得了更好的性能

1、引言

作者提到，自从AlexNet出现以来，卷积神经网络迅速成为视觉任务的主流方法，在相当多的领域有广泛的应用。提升网络性能的方法常常是构造更深、更宽的架构。此外，作者还发现，在分类任务上的性能提升常常可以促进其他任务领域的提升。

相比起VGG及其改进版本，Inception结构要求的计算量低，更适合于大数据场景。然而Inception结构本身的复杂性使得它很难在网络中做出改变。单纯地增加Inception结构的规模会使得计算效率下降。例如，若仅仅将Inception结构中的卷积核的数量变为原来的两倍，那么计算的代价和参数数量都将变为原来的4倍，这在实际的大数据场景下是没有意义的，尤其是在模型性能提升很小的情况下。

故此，作者提出了一些被证明有用的、用于扩展网络结构的一般性准则和优化方法。作者也提到，虽然提出的一般性准则以及优化方法并不仅限于在Inception结构中使用，但是由于Inception本身的降维、并行架构特点，Inception结构对于架构中相邻的组件之间的变化敏感度不高，故此这些准则或优化方法的效果能够在Inception结构中更容易观察到。

2、通用的设计原则

作者基于大量的实验提出了设计卷积网络架构的几点通用准则。

1. 避免特征表达瓶颈，特别是在网络的前几层。通俗来说，从输入层到输出层应该避免特征的极度压缩，各层的特征表示应该缓慢减小。
2. 高维的特征表示更容易在网络中局部处理。增加每个卷积块的激活有利于更多解耦特征，这样能够加快网络的训练；
3. 在低维特征中进行空间聚合嵌入不会对模型的特征表达构成大的影响，例如在进行3x3卷积之前可以使用1x1卷积进行降维（空间聚合），这样做可以降低计算量却不会对特征表达造成影响。关于这一点，作者的推断是相邻神经元之间的强相关性可以使得执行降维操作时信息丢失较少。
4. 平衡网络的深度和宽度。同时增大网络的深度和宽度可以提高模型的性能，但是会带来计算的复杂性。

上述的一般性准则从理论上是可行的，但对于具体的模型架构来说需要进行进一步的实验论证。

3、大滤波器的分解卷积

从卷积的特征输出来看，相邻的激活之间代表了较高的相关性，因此在聚合之前进行空间降维也近似于压缩局部特征。在这篇文章中，作者探究了不同设置下的分解卷积。通过分解卷积在减少参数数量的同时可以得到更多的解耦特征，加快网络的训练。同时，节省下来的空间、计算资源可以用于进一步增加卷积核的尺寸，以达到代价基本不变下的更高性能。

3.1 分解成更小的卷积

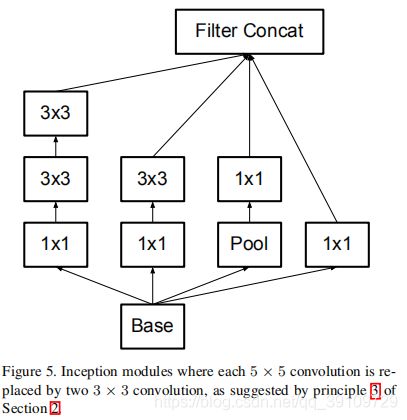
在原始的Inception结构中，作者将5x5卷积使用两层串联的3x3卷积进行替代，在相同的感受野下节省了计算复杂性，并进一步增加了非线性。作者对分解卷积进行了进一步地论证，提出了两个关键的问题：

1. 分解卷积是否会造成特征表达的损失？
2. 如果主要目标是对计算的线性部分进行分解，是否建议在第一层保持线性激活？

作者针对这两个问题进行了控制实验，在进行对比的两个Inception架构中，一个使用分解卷积的两层激活函数分别是linear + Relu, 另一个两层都使用Relu,对比结果如下：

实验结果表明，使用两层Relu激活的分解卷积性能更好，作者将这种提升归因于网络可学习的空间增强了。

3.2 非对称分解卷积

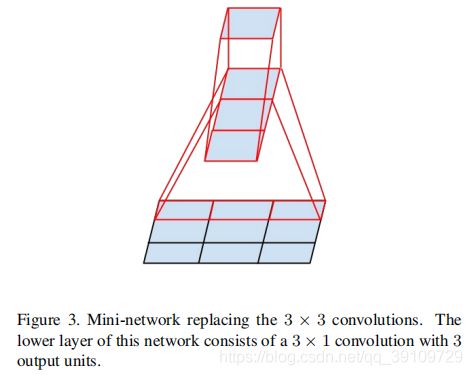
以上所进行的卷积分解都是对称的，作者进一步探讨了非对称的分解卷积方法。做法就是将nxn的卷积变成nx1和1xn串联来代替。例如，3x3的卷积可以被3x1、1x3的卷积替代：

一个3x3的patch经过3x1的卷积以后得到1x3的特征输出，再经过1x3的卷积得到1x1的特征输出，这样相当于直接进行3x3的卷积。通过这样的方式，节省了33%的参数。通用的Inception非对称分解卷积示意如下：

4、使用辅助分类器

在GoogleNet中，作者为了减缓梯度消失，加快模型收敛，在两层Inception输出后使用了两个辅助分类器，详细可参考(论文阅读： Going deeper with convolutions)。作者发现，使用辅助分类器时对训练的初期并没有促进收敛的作用，直到训练后期，使用辅助分类器的效果才凸显出来。

另一方面，作者在实验中移除了较低层次的辅助分类器后，在模型性能上并没有负面影响。这两点表明，使用辅助分类器并不能对低级特征的演化有促进作用。作者在实验中还发现，把辅助分类器的分支改成批量归一化（Batch Normalization)或者加上dropout，可以提升主分类器的性能，因此作者更倾向于将辅助分类器看成是正则化。

5、高效下降特征图尺寸

作者提到，一般来说在CNN中常常会使用一些pooling操作来降低特征图的尺寸，但是为了避免特征表达瓶颈，一般会在pooling前增加卷积核的个数进行stride为1的卷积（其实就是拓展通道数），然而这样做会导致计算量增加。另外一种可能的做法是带卷积的pooling，就是先卷积，再经过卷积拓展通道数。

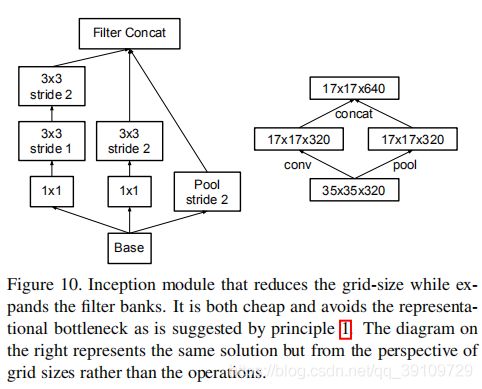
作者给出了两种降低特征图尺寸的方法，左边的方法计算量低，但是违背了原则(1)不能引入特征表达瓶颈，右边的方法计算上更加复杂。（其实我并不是很理解这个特征瓶颈，在我看来表达能力与计算量实在是鱼和熊掌。。。）

随后作者提出了两个模块并行的思路，一个卷积模块C，一个降维模块P,stride都为2，将两个模块同时应用于特征图，再将输出再通道上进行连接。这样相当于将原始的Inception结构内的Pooling(stride 2)改成了右边的并行方案。

6、Inception-v2

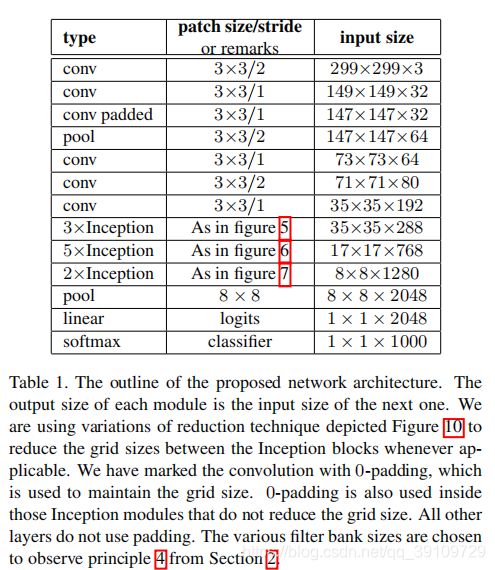
作者基于以上的分析与所提出的通用性准则提出了改进后的Inception-v2架构：

相比起Inception-v1结构，这里将开始的7x7卷积使用3个3x3卷积替代，在后面的Inception模块中分别使用了三种不同的模式：

• 第一部分输入的特征图尺寸为35x35x288,采用了图5中的架构，将5x5以两个3x3代替。
  

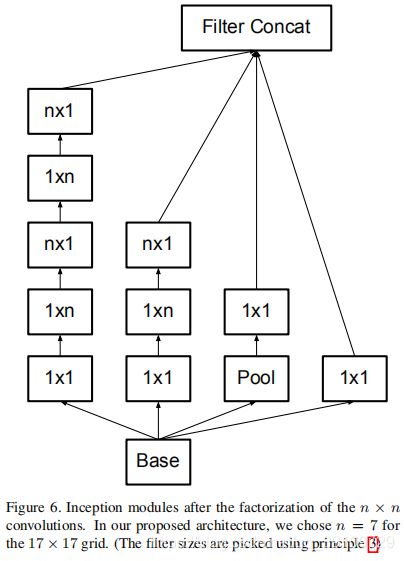
• 第二部分输入特征图尺寸为17x17x768，采用了图6中nx1 + 1xn的结构

• 第三部分输入特征图尺寸为8x8x1280, 采用了图7中所示的并行模块的结构

Inception-v2架构上为42层，计算量只是Inception的2.5倍。

7、通过标签平滑进行模型正则化

作者提出了一种通过向真实数据标签分布加入噪声的方式来进行正则化，抑制过拟合问题。一般地，数据标签都是以One-hot形式编码，正确类别标记为1，错误标签标记为0，使用交叉熵损失函数时，其损失函数为：
$$loss=-\sum _{k=0}^K\log (p(k))q(k)$$
其标签分布是一个狄拉克函数：$$q(k)=\{\begin{array}{ll}0& k=y\\ 1& k\ne y\end{array}$$ , 最小化$loss$ 相当于最大化正确标签的对数似然。而预测分布$p(k)$ 是通过模型得分输出$z_k$ 通过softmax函数得到的，$p(k)\to 1$ 时$loss$最小，但对于有界的$z_k$ 来说无法实现，所以我们只能让正确标签的得分远大于其他标签，即：$z_y>>z_k$ ，则规范后的概率输出会让正确标签的概率远远大于错误标签，这样做会带来两个问题：

• 过拟合：因为模型使得正确标签的概率足够大
• 降低模型的泛化能力

所以作者提出不使用原始的标签概率分布$q(k)$ ，进而考虑标签的真实分布$u(k)$ 与平滑指数 $\epsilon $ 来修正$q(k)$， 得到新的标签概率分布：$$q^{{}^{\prime }}(k)=(1-ϵ)q(k)+ϵu(k)$$ , 一般来说$u(k)$ 为均匀分布， 即
$$q^{{}^{\prime }}(k)=(1-ϵ)q(k)+\frac{ϵ}{K}$$
一般来说$K$ 是类别数， 而$ϵ$ 取值较小，这样就保证了非正确标签的真实概率不为0，这样做的好处是可以防止正确标签的预测概率远远大于错误标签，因为在这种情况下，错误标签的对数$\log (p(k))$ 不能被忽略， 当正确标签的预测概率趋于1，而其他标签的概率趋于0时， 损失函数会是一个很大的值。

作者的实验证明，使用标签平滑归一化（LSR）可以让模型效果有略微提升。

8、训练方法

最优模型的优化方法：RMSProp + learning rate decay(0.9) , 同时使用了阈值为2的梯度截断使得训练更加稳定。

9、在低分辨率输入中的性能

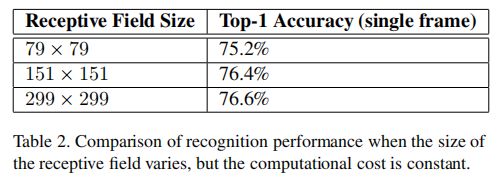
对于一些视觉任务，例如目标检测而言，其中的一个难点就在于在图像中低分辨率的目标难以检测。常规的方法是对这些使用更大感受野来进行卷积，以提高在低分辨率输入上的识别准确率。但是这很难说明性能的提升是来自于感受野的扩大还是模型能力及计算量的增加。所以引出的个问题是在保持计算量不变的情况下，更大的感受野对于模型的性能有多大的影响？ 作者对此进行了实验验证，由此设计了三组实验，三组实验感受野逐步下降而计算量保持不变：

• 299x299的感受野， stride = 2, 加上maxpooling
• 151x151的感受野， strde = 1, 加上maxpooling
• 79x79的感受野， stride = 1, 不进行maxpooling

实验对比了三种不同方式下的准确率：

实验表明虽然感受野增大，但是在保持计算量不变的情况下模型性能相差不大（我觉得还是挺大的。。。）

10、实验及对比

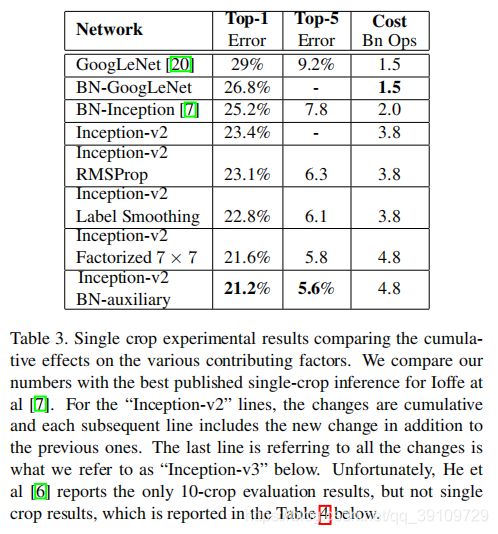
在Inception-v2的基础上，作者逐步加上了RMSprop优化、LSR 与 BN-auxilary, 形成了Inception-v3，在单尺度crop的输入下，最终模型的结果如下：

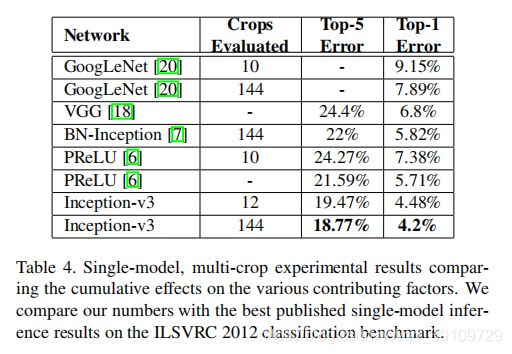
同时也将Inception-v3进行了多尺度的训练，在单模型下的对比结果如下：

进一步地，Inception-v3进行模型融合（ensemble)后与其他模型做对比：

可以看到Inception-v3在分类任务上都获得了更好的性能！

11、结论

这篇文章主要在一下几个方面做出贡献：

1. 改进原有的Inception结构，使得CNN模型在分类任务上获得更高的性能
2. 演示了即使是低分辨率的输入也可以达到较好的识别效果
3. 研究了如何进行有效的分解卷积以及更进一步的降维，在保证性能的前提下节省计算量
4. 低参数、额外正则化、BN辅助分类器和LSN的结合可以在相对较小的数据集上训练高性能的网络模型

参考

1. 论文地址
2. 代码参考