[机器学习与数据分析] 时间序列聚类方法
聚类分析(cluster analysis)简称聚类(clustering),是根据事物自身的特性对被聚类对象进行类别划分的统计分析方法,其目的是根据某种相似度度量对数据集进行划分,将没有类别的数据样本划分成若干个不同的子集,这样的一个子集称为簇(cluster),聚类使得同一个簇中的数据对象彼此相似,不同簇中的数据对象彼此不同,即通常所说的“物以类聚”。
时间序列是数据的一种常见表示形式。对于时间序列处理来说,一个普遍的任务就是比较两个序列的距离 / 相似性。
1、距离 / 相似性度量
要找到相似的时序曲线,并将其聚为一类,需要有方法刻画时间序列的相似性。
在上图四条曲线中,a、b、d是形状相似的;在这三条曲线中,a与b是最相似的两条曲线是因为a、b距离最近。
因此相似的定义:距离最近且形状相似。——对序列之间的距离进行量化来代表其相似度高低。对于长度相同的序列,计算每两点之间的距离然后求和,距离越小相似度越高。
[闵可夫斯基距离]
闵可夫斯基距离是常用的距离度量方法,如上图左边所示,在一一对应的位置上进行对比。给定两条时间序列:![]() 和
和![]() ,距离度量的具体公式如下:
,距离度量的具体公式如下:
当p=1时,表示曼哈顿距离;p=2时,表示欧几里得距离(又称为欧式距离);当p趋近于无穷大时,该距离转换为切比雪夫距离,具体如下式所示:
闵可夫斯基距离比较直观,但是它与数据的分布无关,具有一定的局限性,如果x方向的幅值远远大于y方向的幅值,这个距离公式就会过度被x维度的作用。因此在加算前,需要对数据进行变换(去均值,除以标准差)。这种方法在假设数据各个维度不相关的情况下,利用数据分布的特性计算出不同的距离。如果数据维度之间数据相关,这时该类距离就不合适。
[马氏距离]
若不同维度之间存在相关性和尺度变换等关系,需要使用一种变化规则,将当前空间中的向量变换到另一个可以简单度量的空间中去测量。假设样本之间的协方差矩阵是![]() ,利用矩阵分解(LU分解)可以转换为下三角矩阵和上三角矩阵的乘积:
,利用矩阵分解(LU分解)可以转换为下三角矩阵和上三角矩阵的乘积:![]() 。消除不同维度之间的相关性和尺度变换,需要对样本x做如下处理:
。消除不同维度之间的相关性和尺度变换,需要对样本x做如下处理:![]() 。经过处理的向量就可以利用欧式距离进行度量。
。经过处理的向量就可以利用欧式距离进行度量。
![]()
[DTW距离]
当序列长度不相等时,如何比较两个序列的相似性?这里就需要动态时间规整(Dynamic Time Warping, DTW)方法 ——— 一种将时间规整和距离测度相结合的一种非线性规整技术。主要思想是把未知量均匀地伸长或者缩短,直到与参考模式的长度一致,在这一过程中,未知量的时间轴要不均匀地扭曲或弯折,以使其特征与参考模式特征对正。DTW距离可以帮助我们找到更多序列之间的形状相似。
在时间序列中,需要比较相似性的两段时间序列的长度可能并不相等,在语音识别领域表现为不同人的语速不同。因为语音信号具有相当大的随机性,即使同一个人在不同时刻发同一个音,也不可能具有完全的时间长度;而且同一个单词内的不同音素的发音速度也不同,比如有的人会把“A”这个音拖得很长,或者把“i”发的很短。在这些复杂情况下,使用传统的欧几里得距离无法有效地求的两个时间序列之间的距离(或者相似性)。
动态时间规整是一个计算时间序列之间距离的算法,是为了解决语音识别领域中语速不同的情况下如何计算距离相似度的问题。
相对于用经典的欧式距离来计算相似度而言,DTW在数据点个数不对齐的情况下微调时间从而能够计算距离。DTW之所以能够计算数据点个数不同时间序列之间的距离,是因为DTW方法中时间序列的点可以一对多。
![]()
![]()
如图A所示,实线和虚线分别是同一个词的两个语音波形(在y轴上拉开了,以便观察)。可以看到他们整体上的波形形状很相似,但在时间轴上却是不对齐的。例如在第20个时间点的时候,实线波形的a点会对应于虚线波形的b’点,这样传统的通过比较距离来计算相似性很明显不靠谱。因为很明显,实线的a点对应虚线的b点才是正确的。而在图B中,DTW就可以通过找到这两个波形对齐的点,这样计算它们的距离才是正确的。
即大部分情况下,两个序列整体上具有非常相似的形状,但是这些形状在x轴上并不是对齐的。在比较他们的相似度之前,需要将其中一个(或者两个)序列在时间轴下warping扭曲,以达到更好的对齐。而DTW方法就是实现这种warping扭曲的一种有效方法 —— DTW通过把时间序列进行延伸和缩短,来计算两个时间序列性之间的相似性。
如何知道两个波形是否对齐?即何种warping扭曲是正确合理的?直观上理解为扭曲规整一个序列后可以与另一个序列重合,这时两个序列中所有对应点的距离之和是最小的。从直观上理解,warping扭曲规整的正确性一般指“feature to feature”的对齐。
所以动态时间规整的思想就是:通过对两个时间序列点之间的相似性进行比较(图1黑线),对原始时间序列进行拉伸到相同时间长度(原始时间序列的长度很可能不一致),进而比较两个时间序列的相似性。
动态时间规整要解决的问题就是:找到一条最优的规整路径,其中
,即认为时间序列1的第i个点和时间序列2的第j个点是相似的。所有相似点的距离之和作为规整路径距离,用规整路径距离来衡量两个时间序列的相似性。规整路径距离越小,相似度越高。
具体计算过程如下:
假设,两个时间序列A和B,![]() 。构造一个(n, m)的矩阵,第(i, j)单元记录两个点
。构造一个(n, m)的矩阵,第(i, j)单元记录两个点![]() 之间的欧氏距离,
之间的欧氏距离,![]() 。如上图所示,一条弯折的路径W,由若干个彼此相连的矩阵单元构成,这条路径描述了A和B之间的一种映射。设第k个单元定义为
。如上图所示,一条弯折的路径W,由若干个彼此相连的矩阵单元构成,这条路径描述了A和B之间的一种映射。设第k个单元定义为![]() ,则
,则
![]()
这条弯折的路径满足如下的条件:
- 边界条件:
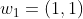 ,且
,且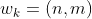 。任何一种语音的发音快慢都有可能变化,但是其各部分的先后次序不可能改变,因此所选的路径必定是从左下角出发,在右上角结束。
。任何一种语音的发音快慢都有可能变化,但是其各部分的先后次序不可能改变,因此所选的路径必定是从左下角出发,在右上角结束。 - 连续性:设
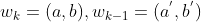 ,那么
,那么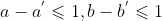 。不可能跨过某个点去匹配,只能和自己相邻的点对齐。这样可以保证Q和C中的每个坐标都在W中出现。
。不可能跨过某个点去匹配,只能和自己相邻的点对齐。这样可以保证Q和C中的每个坐标都在W中出现。 - 单调性(单调递增):设
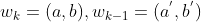 ,那么
,那么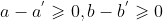 。限制W上面的点必须是随着时间单调进行的。以保证图B中的虚线不会相交。
。限制W上面的点必须是随着时间单调进行的。以保证图B中的虚线不会相交。
在满足上述条件的多条路径中,最短的,花费最少的一条路径是:
DTW距离的计算过程是一个动态规划过程,先用欧式距离初始化矩阵,然后使用如下递推公式进行求解:
![]()
# 规整窗口 #
- 上面DTW计算的时候,路径是点(1,1)出发,向右上角前进。整个矩阵都会扫一遍,所有的点的累加距离都会计算出来。这种情况也叫作DTW, no Warping Window。
- 这样做的缺点是,如果最终的路径是从点(1,1)直线走到(1,F)再直线走到(4,F)。这说明T中的点1会对应R的A-F六个点,然后R中的F再对应T的2-4三个点。这样规整的跨度有点大了,就不再是微调时间序列中时间不对齐。
- 所以又有了DTW with Warping Window,现在规整跨度,效果如下所示。只需稍微改动动态规划的代码的循环范围。
[参数距离]
除了直接的度量原始时间序列之间的距离,很多方法尝试对时间序列进行建模,并比较其模型参数的相似度。之前我们介绍了时间序列的统计分析方法,这里,可以用到的有:
基于相关性的相似度度量方法:
量化两条序列X与Y之间的相关系数:相关系数等于1,表示它们完全一致;如果等于-1,表示它们之间是负相关的。
基于自相关系数的相似度度量方法:
如上式分别抽取曲线X与Y的自相关系数,可以定义时间序列之间的距离如下:
![]()
基于周期性的相似度度量方法:
通过傅里叶变换得到一组参数,然后通过这组参数来反映原始的两个时间序列时间的距离。数学表达为:
还有通过ARMA模型抽象时序(后补)的参数,进行举例度量,类似方法这里不作展开。
2、聚类算法
有了对时间序列的距离度量方法,可以采用机器学习中很多聚类算法,进行时间序列的聚类分析。
[基于距离的机器学习聚类算法]
KMeans 算法是非常经典的距离度量聚类算法,其目的是把样本,基于它们之间的距离公式,把它们划分成K个类别,其中类别K的个数是需要在执行算法之前人为设定的。
从数学语言上来说,假设已知距离空间点集为 ![]() ,事先设定的类别个数是K ,当然 K<=n 是必须要满足的,因为类别的数目不能够多于点集的元素个数。算法的目标是寻找到合适的集合
,事先设定的类别个数是K ,当然 K<=n 是必须要满足的,因为类别的数目不能够多于点集的元素个数。算法的目标是寻找到合适的集合 ![]() 使得
使得
达到最小,其中![]() 表示集合
表示集合![]() 中的所有点的均值。
中的所有点的均值。
[基于相似性的机器学习聚类算法]
层次聚类是一种很直观的方法,就是一层一层的对数据进行聚类操作,可以自低向上进行合并聚类、也可以自顶向下进行分裂聚类。
-
凝聚式:从点作为个体簇开始,每一个步合并两个最接近的簇
-
分裂式:从包含所有个体的簇开始,每一步分裂一个簇,直到仅剩下单点簇为止
所谓凝聚,其大体思想就是在一开始的时候,把点集集合中的每个元素都当做一类,然后计算每两个类之前的相似度,也就是元素与元素之间的距离;然后计算集合与集合之前的距离,把相似的集合放在一起,不相似的集合就不需要合并;不停地重复以上操作,直到达到某个限制条件或者不能够继续合并集合为止。
所谓分裂,正好与聚合方法相反。其大体思想就是在刚开始的时候把所有元素都放在一类里面,然后计算两个元素之间的相似性,把不相似元素或者集合进行划分,直到达到某个限制条件或者不能够继续分裂集合为止。
在层次聚类里面,相似度的计算函数就是关键所在。在这种情况下,可以设置两个元素之间的距离公式,距离越小表示两者之间越相似,距离越大则表示两者之间越不相似。除此之外,还可以设置两个元素之间的相似度。
DTW讲解参考:
- https://zhuanlan.zhihu.com/p/30019607
- https://blog.csdn.net/qq_40006058/article/details/79992255
- https://blog.csdn.net/lin_limin/article/details/81241058
- https://www.cnblogs.com/yifanrensheng/p/12501238.html
- https://mp.weixin.qq.com/s/iusTb9UwKybwJBqd2kSvUA
- https://blog.csdn.net/zb1165048017/article/details/49226315
![[机器学习与数据分析] 时间序列聚类方法_第1张图片](http://img.e-com-net.com/image/info8/5b682d350f954f1b86af387d07838337.jpg)
![[机器学习与数据分析] 时间序列聚类方法_第2张图片](http://img.e-com-net.com/image/info8/d844916eae54467dad3425c021d33488.jpg)
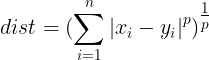
![[机器学习与数据分析] 时间序列聚类方法_第3张图片](http://img.e-com-net.com/image/info8/8fad34915b354f8685d3177e695251ae.jpg)
![[机器学习与数据分析] 时间序列聚类方法_第4张图片](http://img.e-com-net.com/image/info8/c3593453d40b4c10b0ceed8b7aa85141.jpg)
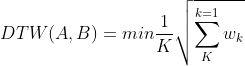
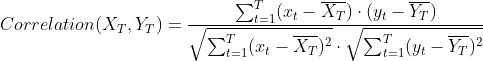
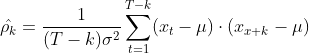

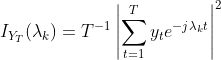
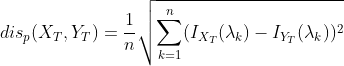
![[机器学习与数据分析] 时间序列聚类方法_第5张图片](http://img.e-com-net.com/image/info8/c121d1c8850643b4b7cdd9963d32a25a.jpg)
![[机器学习与数据分析] 时间序列聚类方法_第6张图片](http://img.e-com-net.com/image/info8/713f9eea4e574366a8ac0049d6d8258e.png)