(TNNLS-2022)步态质量感知网络：面向轮廓步态识别的可解释性

步态质量感知网络：面向轮廓步态识别的可解释性

paper题目：Gait Quality Aware Network: Toward the Interpretability of Silhouette-Based Gait Recognition

paper是北京师范大学发表在TNNLS 2022的工作

paper链接：地址

Abstract

由于步态识别可以在远距离以非侵入性方式进行，并应用于换衣服的情况，因此步态识别越来越受到人们的关注。现有的大多数方法都是以步态序列的轮廓作为输入，从多个轮廓中学习统一的表示，以匹配probe和gallery。然而，这些模型都面临着缺乏可解释性的问题，例如，不清楚步态序列中的哪个轮廓以及人体中的哪个部位对识别相对更重要。在这项工作中，我们提出了一种用于步态识别的步态质量感知网络（GQAN），该网络通过两个block明确评估每个轮廓和每个部分的质量：帧质量块（FQBlock）和部分质量块（PQBlock）。具体而言，FQBlock以压缩和激发方式工作，以重新校准每个轮廓的特征，并将所有通道的分数添加为帧质量指示器。PQBlock预测每个部分的分数，用于计算probe和gallery之间的加权距离。特别的，我们提出了一种部分质量损失（PQLoss），它使GQAN能够以端到端的方式进行训练，只需要序列级标识注释。这项工作对于基于轮廓的步态识别的可解释性具有重要意义，我们的方法在CASIA-B和OUMVLP上也取得了非常有竞争力的性能。

关键词：帧质量，步态质量感知网络（GQAN），部分质量，基于轮廓的步态识别。

I. INTRODUCTION

人类步态作为一种独特的生物特征识别技术，由于可以通过非侵入性的方式远距离获取，因此受到越来越多的关注。步态识别的目的是根据行走模式来识别人的身份，现有的步态识别方法大致可分为基于模型和基于外观两类。基于模型的方法[5]–[7]试图从视频中提取人体结构，其优点是对服装和携带条件具有鲁棒性。然而，在低分辨率条件下，很难准确估计身体参数，这对基于模型的方法有很大的不利影响。相比之下，基于外观的方法[8]–[10]试图从视频中学习步态特征，而无需对人体结构进行明确建模。轮廓简单而有效，通常作为基于外观的方法的输入。

在以前的文献中，基于轮廓的方法 [11]-[13] 具有最先进的步态识别性能；然而，所有这些方法都面临着一个关键挑战，即缺乏可解释性。例如，不清楚步态序列中的哪个轮廓以及人体的哪个部分对于最终识别相对更重要。在实际应用中，图 1 所示的情况经常发生：1）属于不同受试者的两个序列被赋予高相似性分数，2）属于同一受试者的两个序列被赋予低相似性分数。由于缺乏可解释性，很难分析导致这些案例的原因。

图 1. 基于轮廓的步态识别的困难案例说明。 (a) 和 (b) 相似度较低的同一受试者。 (b) 和 © 具有高相似度分数的不同受试者。由于缺乏可解释性，很难分析导致这些案例的原因。 (a) ID = 112。(b) ID = 112。© ID = 123。

在这项工作中，我们专注于基于轮廓的步态识别的可解释性。可解释性是一个广泛的话题，可以从许多不同的方面来解决。据我们所知，之前在深度学习背景下处理可解释性的工作大多试图分析每个神经元的作用 [14]、[15] 并发现输入中的判别区域 [16]。不同的是，在这项工作中，我们试图找出每个轮廓和每个部分对于基于轮廓的步态识别的相对重要性。为此，我们提出了一个步态质量感知网络（表示为 GQAN），它通过两个块（即帧质量块（FQBlock）和部分质量块（PQBlock））明确评估每个轮廓和每个部分的质量。

具体来说，步态序列中的轮廓是相互补充的，并且包含受试者的行走模式。由于遮挡、几何失真、分割错误等，每个轮廓的质量无法得到保证[17]、[18]，这可能会损害从轮廓中学习特征。在 GQAN 中，步态序列的轮廓被视为无序集合。 FQBlock 被提出将每个轮廓的帧质量结合起来进行基于集合的特征学习，可以学习更多的判别特征并增强可解释性。具体来说，FQBlock 以压缩和激发方式 [19] 重新校准每个轮廓的特征，并将所有通道的分数添加为相应轮廓的帧质量指标。

此外，通过水平切片特征来学习部分表示已被广泛用于步态识别[10]-[13]。然而，在计算两个步态序列的距离时，所有部分表示都被同等对待，这对于步态识别来说并不是最优的。例如，在更换外套或夹克的情况下，头部和腿部的特征通常比上身的特征更重要，以匹配probe和gallery。 PQBlock 通过学习每个部分的自适应权重来解决这个问题。它对集合级别的部分表示进行操作，并预测每个部分的分数，以计算probe和gallery之间的加权距离。特别的，我们提出了一个名为部分质量损失（PQLoss）的损失函数来训练仅使用序列级身份注释的 PQBlock。

总之，这项工作的主要贡献在于三个方面。

1. 我们通过明确评估每个轮廓和每个部分的质量，针对基于轮廓的步态识别的可解释性提出了一个 GQAN。 GQAN可以根据相对重要性自动对轮廓和部分进行排序。
2. 我们提出了一种 PQLoss，它使 GQAN 能够以端到端的方式进行训练，只需要序列级的身份注释。
3. GQAN 在所有步行条件下都在 CASIA-B 和 OUMVLP 上取得了非常有竞争力的表现。

II. RELATED WORK

A. Gait Recognition

---

步态识别的方法大致可以分为两类：基于模型的和基于外观的，本节将简要回顾。

基于模型的方法尝试从视频中显式提取人体结构以进行步态识别。例如，PoseGait [6] 将 RGB 帧估计的 3-D 姿态作为步态识别的输入。 OUMVLPPose [5] 构建了一个基于姿态的大规模步态数据集，并评估了步态识别的不同姿态估计方法。 End2EndGait [7] 首先通过拟合 SMPL [20] 提取姿势和形状特征，然后输入识别网络。这些方法在理论上对服装和携带条件是稳健的；然而，它们难以适应难以准确估计人体参数的低分辨率条件。

基于外观的方法试图从视频中学习步态特征，而无需明确地对人体结构进行建模。在大多数情况下，以剪影作为输入，可以适应低分辨率和换衣服的情况。基于剪影的方法可以进一步分为三个子类别：基于模板、基于视频和基于集合。基于模板的方法 [3]、[8]、[21]-[23] 将步态序列的轮廓聚合到模板中，例如步态能量图像 (GEI) [24]，这很简单，但忽略了时间信息。基于视频的方法 [9]、[25]、[26] 将步态序列的轮廓视为视频以提取空间和时间信息，而模型（例如 3-D 卷积神经网络（CNN） [25] 和多时间尺度 3-D (MT3D) [9]) 相对难以训练。基于集合的方法[10]-[13]将每个步态序列的轮廓视为一个无序集，这是基于轮廓的外观也编码了一些时间信息[10]。此外，还有一些工作将其他类型的输入用于基于外观的步态识别，例如 GaitNet [27]（RGB 帧）、GaitMotion [28]（光流）和 SM-Prod [29]（灰色图像和光流）。

我们的工作属于基于外观的方法，其中将每个步态序列的轮廓作为输入并视为无序集合。我们通过明确评估每个轮廓和每个部分的相对重要性来实现基于轮廓的步态识别的可解释性。

B. Unordered Set

---

无序集首先由 PointNet [30] 引入视觉社区，用于 3-D 分类和分割，然后被用于许多其他视觉任务 [10]、[31]-[33]。 GaitSet [10] 首先提出将步态序列的轮廓视为无序集，现在广泛用于基于轮廓的步态识别。在 GQAN 中，步态序列的轮廓也被视为质量评估的无序集。

与我们的工作更相关的是 [31] 和 [32]，它们根据图像质量学习自适应权重，用于基于集合的行人重识别 [31] 和人脸识别 [32]。在 GQAN 中，提出了 FQBlock 来评估每个轮廓的帧质量以进行步态识别，这在三个方面不同于 [31] 和 [32]。首先，我们根据帧质量采用不同的方式获得集合级表示，细节将在第 III-A 节中描述。其次，FQBlock 对不同 bin 的特征持有独立的权重，这些特征是通过水平切片每个轮廓的特征而获得的。第三，我们进一步提出了一个 PQBlock 来评估每个部分的质量以进行步态识别。

III. OUR APPROACH

在这项工作中，我们针对基于轮廓的步态识别的可解释性提出了一个 GQAN。网络结构如图 2 所示。它主要由两个块组成，即 FQBlock 和 PQBlock，以明确评估每个轮廓和每个部分的识别质量。具体来说，FQBlock 以压缩和激发的方式工作，重新校准每个轮廓的特征，并将所有通道的分数添加为帧质量指标。 PQBlock 预测每个部分的分数，以生成自适应权重，用于计算probe和gallery之间的距离。下面，我们将首先介绍 FQBlock 的组成和工作机制。然后我们将描述 PQBlock 的结构以及如何使用它的输出来计算probe和gallery之间的距离。最后，将展示一个 PQLoss，它使 GQAN 能够仅使用序列级身份注释进行训练。

图 2. GQAN 示意图。编码器主要由卷积层组成，分别从每个轮廓中提取特征。 FQBlock 用于评估每个轮廓的质量，其中其权重在轮廓之间共享，但对于不同的 bin（由不同的颜色注释）是独立的。 PQBlock 对集合级零件表示进行操作并预测分数以分别评估每个零件。

A. Frame Quality

---

步态序列的轮廓包含受试者的行走模式，并且相互补充。但由于遮挡、几何变形、分割错误等多种因素，无法保证每个轮廓的质量，对步态特征学习产生不利影响。在 GQAN 中，提出了 FQBlock 来解决这个问题，其中每个轮廓的质量可以自动学习，尽管在训练中没有明确提供这种监督。

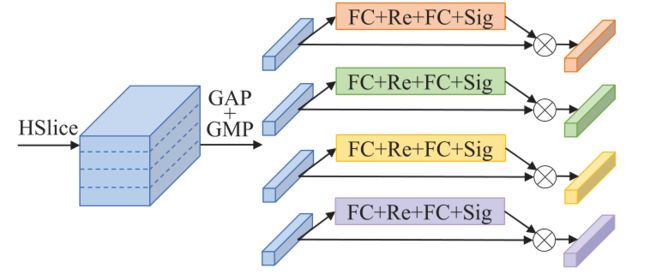
具体来说，FQBlock 以挤压缩和激发风格 [19] 工作，主要由两个完全连接的层组成，然后分别是整流线性单元 (ReLU) 和 sigmoid。首先采用全局平均池化（GAP）和全局最大池化（GMP）来压缩每个通道中的信息。然后采用两个全连接层进行激励，以自适应地重新校准每个轮廓的特征。特别是，考虑到从头到脚的轮廓形状差异很大，FQBlock 将每个轮廓的特征水平且均等地分割到多个 bin 中，并为不同的 bin 保持独立的权重。 FQBlock 的结构如图 3 所示，为了便于说明，轮廓级特征被水平分成四个 bin。

图3. FQBlock的图示。HSlice表示水平切片，GAP表示全局平均池，GMP表示全局最大池，FC表示全连接层，Re表示ReLU，Sig表示sigmoid。

公式上，$G$表示由$N$个轮廓组成的步态序列，$F=\left\{F_1,F_2,\dots ,F_N\right\}$表示从每个轮廓中提取的特征。 FQBlock 首先将每个轮廓的特征水平均等地分割成$S$个 bin（例如，$S=$16），表示为$F_{i j}(i \in[1,2, \ldots, N], j \in$ $[1,2,\dots ,S])$。然后，$F_{ij}$，即第$i$个轮廓和第$j$个 bin 的特征，处理如下：
$$\begin{array}{rl}{X}_{ij}& =\mathrm{GAP}\left(F_{ij}\right)+\mathrm{GMP}\left(F_{ij}\right)\\ Y_{ij}& =\sigma \left(W_j^2\delta \left(W_j^1{X}_{ij}\right)\right)\\ Z_{ij}& =X_{ij}\otimes Y_{ij}\end{array}$$
其中 GAP 和 GMP 是沿空间维度的挤压操作，$W_j^1$和$W_j^2$表示两个全连接层的激励权重，$\delta$表示 ReLU 函数，$\sigma$表示 sigmoid 函数，$\otimes$表示元素乘法。最后，得到第$j$个 bin 的集合级表示如下：
$$P_j=\mathrm{Set}\mathrm{Pool}\left(Z_{1j},Z_{2j},\dots ,Z_{Nj}\right)(4)$$
其中 SetPool 表示集合池化以聚合无序集合 [30] 中的特征，并通过沿集合维度的最大池化来实现。特别是，我们使用$Y_{ij}$重新校准特征并沿通道维度添加$Y_{ij}$作为第$i$个轮廓和第$j$个区域的帧质量指标。

值得注意的是，squeeze-and-excitation 风格最早是在squeeze-and-excitation network (SENet) [19] 中提出的，FQBlock 在三个方面与其不同。首先，SENet 被提出用于单张图像分类，而 FQBlock 被提出来评估无序集中的帧质量，并将 FQBlock 的中间输出作为每个剪影的帧质量指标。其次，FQBlock 采用 GAP 和 GMP 来压缩每个通道中的信息。第三，FQBlock 对不同 bin 的特征持有独立的权重，以处理轮廓中较大的形状变化。此外，注意力机制广泛应用于动作识别领域[34]-[36]。具体来说，[34] 和 [35] 中的方法使用循环模型来发现连续帧中的代表区域，而 FQBlock 主要由两个全连接层组成，并处理无序集。自注意力网络 (SAN) [36] 使用自注意力机制 [37] 来捕获不同帧之间的位置和运动的相关性，而 FQBlock 处理每个轮廓的质量，随后的 PQBlock 处理每个轮廓的质量步态序列的一部分。值得注意的是，提出的质量模块不同于流行的自注意力机制[37]。例如，对于自注意力机制至关重要的查询、键和值的向量不包含在我们的方法中。

B. Part Quality

---

对特征进行水平等分切片以获得部分表示已被广泛用于步态识别[10]-[12]。为了保持符号的一致性，我们使用$P_j(j\in [1,2,\dots ,S])$来表示从步态序列$G$中提取的集合级第$j$部分表示，它是通过应用$1\times 1$卷积获得的$P_j$由(4) 输出。然后，两个步态序列（表示为$G_1$和$G_2$）的距离计算为
$$D_{\mathrm{e}\mathrm{q}}\left(G_1,G_2\right)=\frac{1}{S}\sum _{j=1}^{S}D\left(P_j^{G_1},P_j^{G_2}\right)(5)$$
其中$S$是部分的数量，$D()$测量两个部分表示的距离，例如，欧几里德距离。所有部分都被平等对待，这对于步态识别不是最佳的。例如，在更换外套或夹克的情况下，与上半身相比，头部和腿部应分配更大的重量。在 GQAN 中，提出了 PQBlock 来学习每个部分的自适应权重以匹配步态序列。

PQBlock 的结构简单而有效，它由一个全连接层和一个 Sigmoid 函数组成。它对集合级别的部分表示进行操作，并预测一个分数以评估每个部分的相对重要性。全连接层的权重对于不同的部分是独立的。公式上，对于第$j$部分，将 (4) 中的$P_j$作为输入，输出得分$q_j$计算为
$$q_j=\sigma \left(M_j{P}_j\right)$$
其中$M_j$表示全连接层的权重，$\sigma$表示 sigmoid 函数。然后，$G_1$和$G_2$的距离计算为
$$D_{\mathrm{a}\mathrm{d}\mathrm{a}}\left(G_1,G_2\right)=\frac{1}{{\sum }_{j=1}^S{q}_j^{G_1}{q}_j^{G_2}}\sum _{j=1}^S{q}_j^{G_1}{q}_j^{G_2}D\left(P_j^{G_1},P_j^{G_2}\right)(7)$$
其中$q_j^{G_1}$和$q_j^{G_2}$分别是$G_1$和$G_2$第$j$部分的 PQBlock 的预测分数。通过这种方式，不同的部分被自适应地加权以用于两个步态序列的距离计算。

C. Part Quality Loss

---

GQAN 的一个关键挑战是如何训练 PQBlock。当前的步态数据集 [17]、[18] 仅提供序列级身份注释，无法手动注释每个部分的权重。为了解决这个问题，我们提出了一种 PQLoss，它使 PQBlock 能够仅使用序列级身份注释进行训练。

在介绍 PQLoss 之前，我们首先回顾一下在度量学习文献中广泛使用的一些名词，包括 anchor、positive、n d negative [38]、[39]。传统上，anchor-positive 表示属于同一类的两个样本，而 anchor-negative 表示属于不同类的两个样本。在这项工作中，我们使用anchor-positive 来表示属于同一受试者的两个步态序列，并且使用anchor-negative 来表示属于不同受试者的两个步态序列。 PQLoss的核心思想是让anchorpositive在特征空间更近，anchor-negative更远。

公式上，PQLoss 计算如下：
$L_{pq}$
$=\frac{1}{N_{{\mathrm{a}\mathrm{p}}^{+}}}{\sum }_{l\left(G_1\right)=l\left(G_2\right)}{\left[m_{\mathrm{a}\mathrm{p}}+D_{\mathrm{a}\mathrm{d}\mathrm{a}}\left(G_1,G_2\right)-D_{\mathrm{e}\mathrm{q}}\left(G_1,G_2\right)\right]}_{+}$
$+\frac{1}{N_{{\mathrm{a}\mathrm{n}}^{+}}}{\sum }_{l\left(G_1\right)\ne l\left(G_3\right)}{\left[m_{\mathrm{a}\mathrm{n}}+D_{\mathrm{e}\mathrm{q}}\left(G_1,G_3\right)-D_{\mathrm{a}\mathrm{d}\mathrm{a}}\left(G_1,G_3\right)\right]}_{+}(8)$

其中第一项鼓励具有自适应权重的anchor-positive的距离小于具有相同权重的距离，第二项鼓励具有自适应权重的anchor-negative的距离大于具有相同权重的距离。$l()$表示步态序列的标识标签，$N_{{\mathrm{a}\mathrm{p}}^{+}}$和$N_{{\mathrm{a}\mathrm{n}}^{+}}$分别是导致非零损失项的 anchorpositive 和 anchor-negative 对的数量，$m_{\mathrm{a}\mathrm{p}}$和$m_{\mathrm{a}\mathrm{n}}$是避免纠正“已经正确”对的边际阈值。可以观察到，PQLoss 的计算只需要序列级别的标注，每个部分的相对重要性可以自动学习。

D. Training and Evaluation

---

GQAN 被提议通过 FQBlock 和 PQBlock 明确评估每个轮廓和每个部分的质量来增强基于轮廓的步态识别的可解释性。提出了一种 PQLoss，以使仅使用序列级身份注释来训练 GQAN 变得可行。此外，我们为 GQAN 设计了一个高效且有效的骨干网。主干类似于 GaitSet [10]，修改细节将在第 IV-A 节中提供。在本节中，我们将分别介绍 GQAN-Backbone 和 GQAN 的训练和评估，构成一个公平的比较。

1. GQAN-Backbone 的训练和评估：对于 GQAN-Backbone 的训练，表示为$L_1$的损失由三元组损失 $L_{\mathrm{t}\mathrm{p}}$和交叉熵损失$L_{\mathrm{c}\mathrm{e}}$组成。

首先，根据每个部分的特征计算三元组损失$L_{\mathrm{t}\mathrm{p}}$。形式上，对于第$j$部分，$L_{\mathrm{t}\mathrm{p}}^j$计算为
KaTeX parse error: Undefined control sequence: \substack at position 62: …+}}^{j}} \sum_{\̲s̲u̲b̲s̲t̲a̲c̲k̲{l\left(G_{1}\r…
其中$N_{{\mathrm{t}\mathrm{p}}^{+}}^j$是导致第$j$个部分的非零项的三元组数，$m$是边际阈值，$L_{\mathrm{t}\mathrm{p}}$是通过对所有部分的$L_{\mathrm{t}\mathrm{p}}^j$进行平均获得的。值得注意的是，与在part-level距离上计算的$L_{\mathrm{t}\mathrm{p}}^j$不同，(8)中的$L_{pq}$是在sequence-level距离上计算的，$L_{pq}$由分别anchor-positive和anchor-negative的距离的两项组成对。

其次，交叉熵损失 Lce 的计算方式与图像分类 [40]、[41] 的计算方式相似。在我们的实验中，它将所有部分的连接特征作为输入，并将训练集中的每个受试者视为一个单独的类。为简单起见，这里省略了$L_{\mathrm{c}\mathrm{e}}$的计算；详见[12]。

最后，训练 GQAN-Backbone 的损失$L_1$计算为
$$L_1=L_{\mathrm{t}\mathrm{p}}+\alpha L_{\mathrm{c}\mathrm{e}}$$
其中$\alpha$是平衡这两项的损失权重。

对于 GQAN-Backbone 的评估，我们计算所有部分的平均欧几里德距离以匹配probe和gallery，如 (5) 所示。

2. GQAN 的训练和评估：对于包括 FQBlock 和 PQBlock 的 GQAN 的训练，表示为$L_2$的损失由交叉熵损失$L_{\mathrm{c}\mathrm{e}}$和三元组损失$L_{\mathrm{t}\mathrm{p}}$以及 (8) 所示的 PQLoss $L_{pq}$组成。
   $$L_2=L_{\mathrm{t}\mathrm{p}}+\alpha L_{\mathrm{c}\mathrm{e}}+\beta L_{pq}$$
   其中$\beta$是 PQLoss 的损失权重。

对于 GQAN 的评估，我们计算probe和gallery之间的欧几里得距离，其中部分自适应加权，如 (7) 所示。