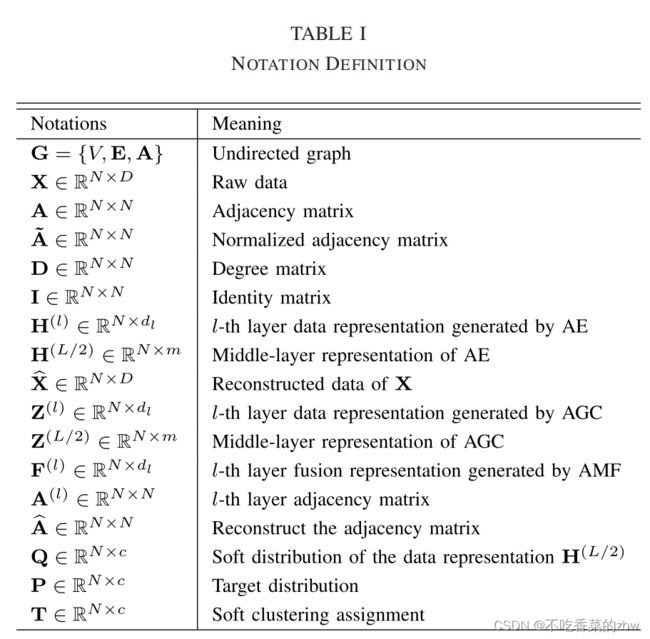
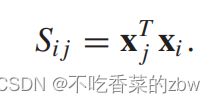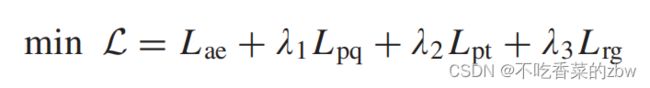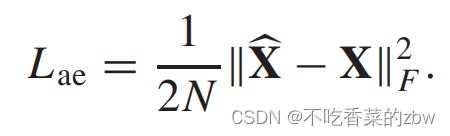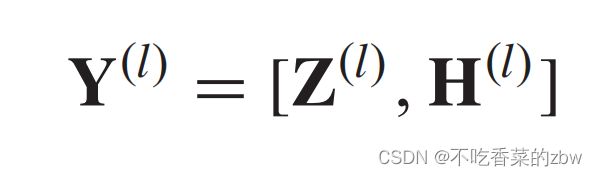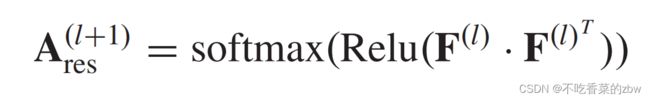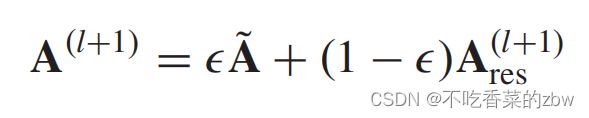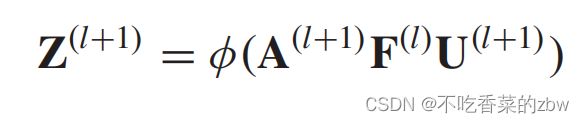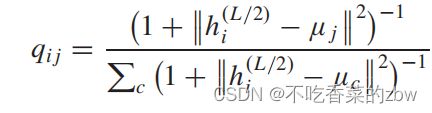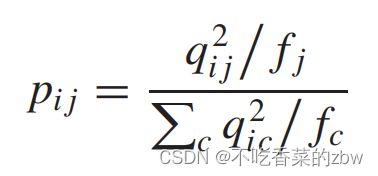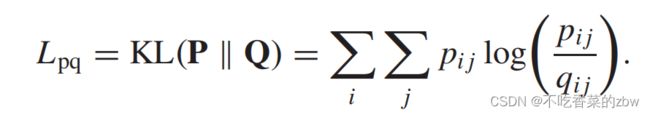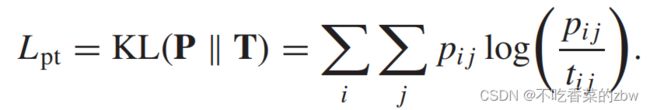论文阅读 Parallelly Adaptive Graph Convolutional Clustering Model(TNNLS2022)

论文标题

Parallelly Adaptive Graph Convolutional Clustering Model

论文作者、链接

作者：

He, Xiaxia and Wang, Boyue and Hu, Yongli and Gao, Junbin and Sun, Yanfeng and Yin, Baocai

链接：Parallelly Adaptive Graph Convolutional Clustering Model | IEEE Journals & Magazine | IEEE Xplore

代码：GitHub - HeXiax/AGCC

---

Introduction逻辑（论文动机&现有工作存在的问题）

无监督学习、聚类——其中的谱聚类spectral clustering，目标是学习一个针对原始数据的好的关联矩阵——与深度学习的结合可以使其学到更好的关联矩阵——这些深度聚类方法，仅仅利用数据的特征信息，很少去利用数据之间的拓扑关系

图谱可以反映数据之间的拓扑关系，这可以提供更具有区别度的信息——有些研究试图将数据之间的拓扑关系与特征信息结合起来，得到所谓的图结构数据graph-structured data。图卷积网络GCN可以处理图结构数据，但仍有以下缺点：1）同质性homophily，反映了图结构是否精确地描述了结点之间的关系。由非图结构数据导出的图结构来描述数据之间的关系是不准确的。并且图结构数据中的自然图谱常常包含了噪音和异常值；2）过度平滑。一组堆叠的深度卷积层往往对一个结点及其邻居结点的特征过度的平滑；3）鲁棒性。图卷积网络往往在图结构数据上表现好，自编码器则在非图数据上表现好，但如何有效的结合这两者，仍是一个问题

本文设计了AGCC算法，主要分成4个模块：1）AE模块，用来从原始数据提取结点的有意义的特征；2）AGC自适应图卷积模块，从融合特征中捕捉结点之间的成对的相关性，用来一层层更新图结构层，然后聚合邻居结点的特征；3）AMF基于融合的注意力机制，收益于AGC和AE，AMF学习他们的融合特征，去获得结点自身以及其邻居的信息，由此这种复杂的融合信息的机制可以获得更精确的结点关系描述；4）SSC引导网络以无监督的形式进行参数优化

论文核心创新点

1.提出了名为AGCC的平行深度聚类方法

2.设计了AGC网络，交替更新图结构以及数据表达，以增强原始图谱的质量和传播优化的数据表达

3.AMF模块利用了AGC和AE的优点，去学习更全面的融合特征

4.重构了样本以及图谱关系，维持了结构信息以及潜在表达

---

相关工作

图卷积网络

深度子空间聚类

---

论文方法

预备知识

 给定一组原始数据，其中分别代表样本数量和特征维度。我们使用KNN来构建一个无向图。在图中。结点集合包括个结点，以及边集合代表点与点之间的独立性。图的拓扑结构可以用一个邻接矩阵表示，其中代表结点之间的链接关系。若，则有，否则有。关联度矩阵为，其中。我们得到，通过标准的与，其中是单位矩阵。

我们也基于一个给定的相似性尺度，来使用KNN去构建邻接矩阵。对于每一个样本，根据相似性矩阵进行度量，个有最高相似性得分的样本被选择成为其的邻居结点，将它们相连起来得到一个无向图。

使用以下的两种方法来计算相似性矩阵：

热力核方法被用来计算图像数据之间的相似性，公式如下：

 样本之间的内积用来计算自然语言数据之间的相似性，公式如下：

 设计动机

收益于GNN的强大的结构捕捉的能力，大量的基于GNN的方法被设计出来并且取得了不错的效果。这些方法的成功要求数据集满足同质性homophily。但是实际情况中，难以满足这个条件。图谱可能缺少好多样本之间的链接，或者是将一些不相似的特征相连起来了，这对图特征学习的影响很大。

首先，我们设计了AGC模块，去交替地一层一层地调整图结构和数据特征，去增强原始图谱结构的质量。其次，一个AMF模块被提出，集成了AGC和AE和针对异构特征的注意力权重，去学习更复杂的融合特征，这促使构建一个好的图片图谱结构。

全局网络结构

如图1所示，分成四个主要的部分。

1）AE模块，提取数据的特征信息，即，。

2）AMF模块：有效地结合AE和AGC模块提取到的特征表达，即，，其中是学到的参数。随后，融合特征被传到下一个AGC层。

3）AGC模块：从融合的特征表示以及聚合的邻居结点的特征中，捕捉结点之间的成对相关性，即，，其中代表激活函数。

4）SSC模块：最小化数据特征表示之间的KL散度及其高置信度的分布，用此来监督AGCC的更新过程。

目标函数

目标函数由AE的重构损失，AGC中的图重构损失，SCC的损失构成，如下所示：

 其中是超参。

Auot-Encoder模块

使用AE来提取输入数据的潜在特征信息，然后将学到的信息一层层的传递到AGC模块中。

假设AE中的编码器有数量为的全连接层，其将原始数据映射到低维特征表达中。对于第层的编码器，第层的特征表达映射到通过以下公式：

 其中，分别代表第层的权重矩阵和偏置。输入数据为原始数据，即。代表非线性激活函数，我们选择了RELU。

AE的解码器使用了与编码器对称的设计，将数据从潜在表达重构成原始数据。因此，解码器的最后一层记为：

 至此，我们得到了一组数据表达。

为了尽可能的保留原始数据的特征，我们最小化原始数据和重构数据之间的重构误差，公式如下：

 基于注意力机制的融合模块

 AE模块目标是从原始数据中提取抽象的数据表达，与此同时AGC模块在更新后的图结构的帮助下，将邻居结点特征进行聚合，以学习更具有区分度的数据表达。

所以，为了充分利用这两个模块去学习更复杂的融合特征，我们设计了AMF模块，如图2所示，对AGC模块和AE模块学习到的数据表示进行逐层加权和融合。由此，可以学习到更全面的融合特征，特征中包括本身及其邻居的信息，可以构成更好的相似性结构。

AMF模块主要由三个全连接层和一个softmax层构成，目标是给AE和AGC学到的特征表达分配更合适的权重。具体来说，对于第层，我们将从AE中学到的数据表达和AGC模块学到的数据特征进行一个融合，公式如下：

 其中，表示链接操作。

得到了链接特征，我们根据的对应重要性以及得到的融合特征，计算其权重，公式如下：

 其中学到的权重为。另外，代表一个三层的全连接层，并且是一个矫正系数。sigmoid函数以及矫正系数可以视为避免模型崩溃的trick。

自适应图卷积模块

现实世界中的图结构通常会被噪音以及异常值所污染，可能在GCN的信息传递中传递误导信息。传统的基于GCN的方法难以去处理被污染的图结构，于是他们给的是固定的图谱。

AGC模块为了解决该问题，交替的逐层对图结构和特征表达层进行更新，以增强图结构的质量，并且对最优的数据表达进行反向传播。

特别地，我们将融合特征输入到对应的AGC模块中，高度结构化的数据信息会被自适应图卷积操作捕捉到。

同一个簇中的结点应该有相似的特征表达，根据结点特征表达构建的相似性图能更好的描述结点之间的关系。为了获得第层的自适应图谱，我们计算了融合特征的内积来构建邻接矩阵，公式如下：

 其中，使用softmax函数来对邻接矩阵进行正则化，这可以减小计算复杂度。

于此同时，原始的邻接矩阵仍然包含大量有用的图结构信息，于是我们将学习到的自适应图与原始图相加，以更新图拓扑结构，公式如下：

 其中，是平衡参数。

因此，对于AGC的第层，卷积操作可以被解释为：

 其中，表示激活函数，代表第层的AGC层的权重矩阵，而则是第层的AGC层的更新的数据表达。

值得注意的是吗，AGC的第一次与其他的不同，第一层将原始数据作为输入，即：

 在多层自适应图卷积操作后，AGC模块将特征信息、结构信息，映射到用于聚类的高效数据表示。

图结构的数据包含两部分的信息：数据特征，其对应的图结构。简单的使用特征重构损失函数不能保存图结构数据的全部信息，忽略了大量的结构信息。因此，为了进一步保存潜在数据特征中的结构化信息，我们进一步设计了图重构损失，如下：

其中，是更具AGC的最后一层的数据表达 内积得到的，即，。

比起传统的GCN，我们提出的AGC模块可以自适应的捕捉结点与融合特征之间的逐对的相关性，可以有效的减轻图中的噪音以及异常值所带来的影响。

自监督聚类模块

我们选择了学生t分布作为核函数，去计算学到的特征以及聚类结果之间的相似性。于是，关于数据特征的原始概率分布为：

 其中，是通过在数据特征上使用K-means得到的初始簇中心。

根据上面的公式，我们得到将第个样本分配给第个簇的概率，即，软分布。为了得到聚类友好的嵌入特征，我们对中的进行平方和归一化，以关注高置信度的样本。辅助目标分布的计算方式如下：

 其中，是软簇概率，将所有样本属于第个簇的概率求和。可以视为软标签的ground-truth。

为了增加聚类的纯洁性以及是得嵌入表达更加靠近真实的簇中心，我们使用KL散度来迫使软分布复合目标分布，公式如下：

 相似的，我们可以根据AGC模块中间层学到的潜在数据表达学习到软簇分布，然后通过最小化和之间的KL散度对进行监督学习，公式如下：

---

消融实验设计

对每一个模块进行消融